[I wrote this after attending a conference six months ago. At the time I was confused about whether and when I was allowed to publish it. I am still confused, but less optimistic about that confusion getting resolved, so I will go ahead and beg forgiveness if I am guessing wrongly. All references to “recently” are as of six months ago.]
Is scientific progress slowing down? I recently got a chance to attend a conference on this topic, centered around a paper by Bloom, Jones, Reenen & Webb (2018).
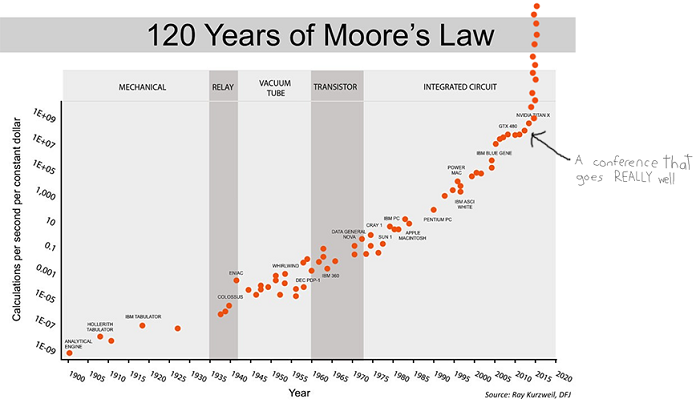
BJRW identify areas where technological progress is easy to measure – for example, the number of transistors on a chip. They measure the rate of progress over the past century or so, and the number of researchers in the field over the same period. For example, here’s the transistor data:
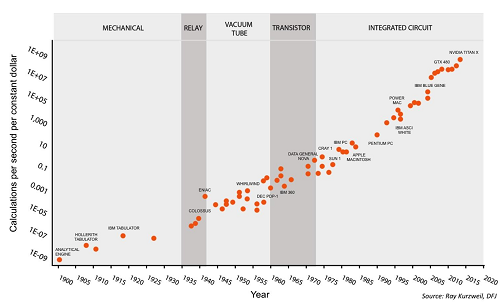
This is the standard presentation of Moore’s Law – the number of transistors you can fit on a chip doubles about every two years (eg grows by 35% per year). This is usually presented as an amazing example of modern science getting things right, and no wonder – it means you can go from a few thousand transistors per chip in 1971 to many million today, with the corresponding increase in computing power.
But BJRW have a pessimistic take. There are eighteen times more people involved in transistor-related research today than in 1971. So if in 1971 it took 1000 scientists to increase transistor density 35% per year, today it takes 18,000 scientists to do the same task. So apparently the average transistor scientist is eighteen times less productive today than fifty years ago. That should be surprising and scary.
But isn’t it unfair to compare percent increase in transistors with absolute increase in transistor scientists? That is, a graph comparing absolute number of transistors per chip vs. absolute number of transistor scientists would show two similar exponential trends. Or a graph comparing percent change in transistors per year vs. percent change in number of transistor scientists per year would show two similar linear trends. Either way, there would be no problem and productivity would appear constant since 1971. Isn’t that a better way to do things?
A lot of people asked paper author Michael Webb this at the conference, and his answer was no. He thinks that intuitively, each “discovery” should decrease transistor size by a certain amount. For example, if you discover a new material that allows transistors to be 5% smaller along one dimension, then you can fit 5% more transistors on your chip whether there were a hundred there before or a million. Since the relevant factor is discoveries per researcher, and each discovery is represented as a percent change in transistor size, it makes sense to compare percent change in transistor size with absolute number of researchers.
Anyway, most other measurable fields show the same pattern of constant progress in the face of exponentially increasing number of researchers. Here’s BJRW’s data on crop yield:
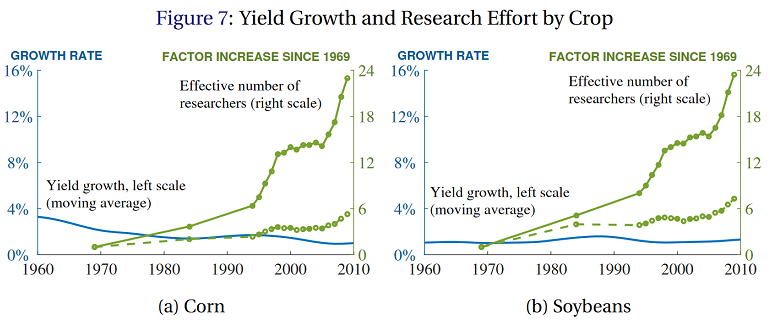
The solid and dashed lines are two different measures of crop-related research. Even though the crop-related research increases by a factor of 6-24x (depending on how it’s measured), crop yields grow at a relatively constant 1% rate for soybeans, and apparently declining 3%ish percent rate for corn.
BJRW go on to prove the same is true for whatever other scientific fields they care to measure. Measuring scientific progress is inherently difficult, but their finding of constant or log-constant progress in most areas accords with Nintil’s overview of the same topic, which gives us graphs like
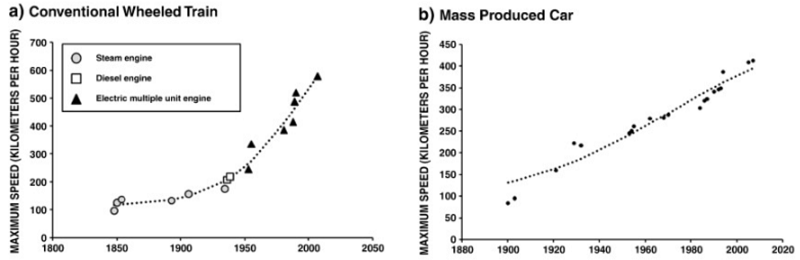
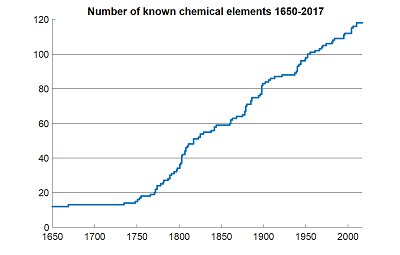
…and dozens more like it. And even when we use data that are easy to measure and hard to fake, like number of chemical elements discovered, we get the same linearity:
Meanwhile, the increase in researchers is obvious. Not only is the population increasing (by a factor of about 2.5x in the US since 1930), but the percent of people with college degrees has quintupled over the same period. The exact numbers differ from field to field, but orders of magnitude increases are the norm. For example, the number of people publishing astronomy papers seems to have dectupled over the past fifty years or so.
BJRW put all of this together into total number of researchers vs. total factor productivity of the economy, and find…
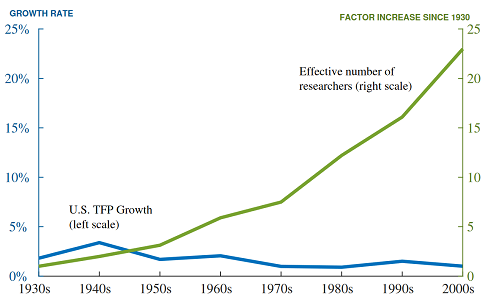
…about the same as with transistors, soybeans, and everything else. So if you take their methodology seriously, over the past ninety years, each researcher has become about 25x less productive in making discoveries that translate into economic growth.
Participants at the conference had some explanations for this, of which the ones I remember best are:
1. Only the best researchers in a field actually make progress, and the best researchers are already in a field, and probably couldn’t be kept out of the field with barbed wire and attack dogs. If you expand a field, you will get a bunch of merely competent careerists who treat it as a 9-to-5 job. A field of 5 truly inspired geniuses and 5 competent careerists will make X progress. A field of 5 truly inspired geniuses and 500,000 competent careerists will make the same X progress. Adding further competent careerists is useless for doing anything except making graphs look more exponential, and we should stop doing it. See also Price’s Law Of Scientific Contributions.
2. Certain features of the modern academic system, like underpaid PhDs, interminably long postdocs, endless grant-writing drudgery, and clueless funders have lowered productivity. The 1930s academic system was indeed 25x more effective at getting researchers to actually do good research.
3. All the low-hanging fruit has already been picked. For example, element 117 was discovered by an international collaboration who got an unstable isotope of berkelium from the single accelerator in Tennessee capable of synthesizing it, shipped it to a nuclear reactor in Russia where it was attached to a titanium film, brought it to a particle accelerator in a different Russian city where it was bombarded with a custom-made exotic isotope of calcium, sent the resulting data to a global team of theorists, and eventually found a signature indicating that element 117 had existed for a few milliseconds. Meanwhile, the first modern element discovery, that of phosphorous in the 1670s, came from a guy looking at his own piss. We should not be surprised that discovering element 117 needed more people than discovering phosphorous.
Needless to say, my sympathies lean towards explanation number 3. But I worry even this isn’t dismissive enough. My real objection is that constant progress in science in response to exponential increases in inputs ought to be our null hypothesis, and that it’s almost inconceivable that it could ever be otherwise.
Consider a case in which we extend these graphs back to the beginning of a field. For example, psychology started with Wilhelm Wundt and a few of his friends playing around with stimulus perception. Let’s say there were ten of them working for one generation, and they discovered ten revolutionary insights worthy of their own page in Intro Psychology textbooks. Okay. But now there are about a hundred thousand experimental psychologists. Should we expect them to discover a hundred thousand revolutionary insights per generation?
Or: the economic growth rate in 1930 was 2% or so. If it scaled with number of researchers, it ought to be about 50% per year today with our 25x increase in researcher number. That kind of growth would mean that the average person who made $30,000 a year in 2000 should make $50 million a year in 2018.
Or: in 1930, life expectancy at 65 was increasing by about two years per decade. But if that scaled with number of biomedicine researchers, that should have increased to ten years per decade by about 1955, which would mean everyone would have become immortal starting sometime during the Baby Boom, and we would currently be ruled by a deathless God-Emperor Eisenhower.
Or: the ancient Greek world had about 1% the population of the current Western world, so if the average Greek was only 10% as likely to be a scientist as the average modern, there were only 1/1000th as many Greek scientists as modern ones. But the Greeks made such great discoveries as the size of the Earth, the distance of the Earth to the sun, the prediction of eclipses, the heliocentric theory, Euclid’s geometry, the nervous system, the cardiovascular system, etc, and brought technology up from the Bronze Age to the Antikythera mechanism. Even adjusting for the long time scale to which “ancient Greece” refers, are we sure that we’re producing 1000x as many great discoveries as they are? If we extended BJRW’s graph all the way back to Ancient Greece, adjusting for the change in researchers as civilizations rise and fall, wouldn’t it keep the same shape as does for this century? Isn’t the real question not “Why isn’t Dwight Eisenhower immortal god-emperor of Earth?” but “Why isn’t Marcus Aurelius immortal god-emperor of Earth?”
Or: what about human excellence in other fields? Shakespearean England had 1% of the population of the modern Anglosphere, and presumably even fewer than 1% of the artists. Yet it gave us Shakespeare. Are there a hundred Shakespeare-equivalents around today? This is a harder problem than it seems – Shakespeare has become so venerable with historical hindsight that maybe nobody would acknowledge a Shakespeare-level master today even if they existed – but still, a hundred Shakespeares? If we look at some measure of great works of art per era, we find past eras giving us far more than we would predict from their population relative to our own. This is very hard to judge, and I would hate to be the guy who has to decide whether Harry Potter is better or worse than the Aeneid. But still? A hundred Shakespeares?
Or: what about sports? Here’s marathon records for the past hundred years or so:
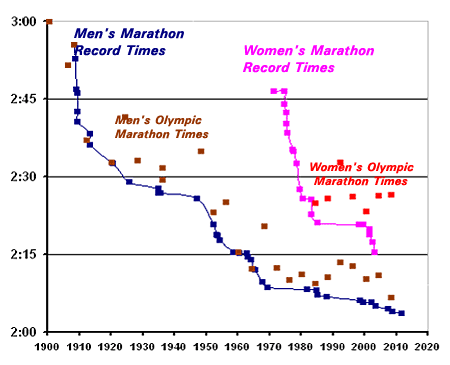
In 1900, there were only two local marathons (eg the Boston Marathon) in the world. Today there are over 800. Also, the world population has increased by a factor of five (more than that in the East African countries that give us literally 100% of top male marathoners). Despite that, progress in marathon records has been steady or declining. Most other Olympics sports show the same pattern.
All of these lines of evidence lead me to the same conclusion: constant growth rates in response to exponentially increasing inputs is the null hypothesis. If it wasn’t, we should be expecting 50% year-on-year GDP growth, easily-discovered-immortality, and the like. Nobody expected that before reading BJRW, so we shouldn’t be surprised when BJRW provide a data-driven model showing it isn’t happening. I realize this in itself isn’t an explanation; it doesn’t tell us why researchers can’t maintain a constant level of output as measured in discoveries. It sounds a little like “God wouldn’t design the universe that way”, which is a kind of suspicious line of argument, especially for atheists. But it at least shifts us from a lens where we view the problem as “What three tweaks should we make to the graduate education system to fix this problem right now?” to one where we view it as “Why isn’t Marcus Aurelius immortal?”
And through such a lens, only the “low-hanging fruits” explanation makes sense. Explanation 1 – that progress depends only on a few geniuses – isn’t enough. After all, the Greece-today difference is partly based on population growth, and population growth should have produced proportionately more geniuses. Explanation 2 – that PhD programs have gotten worse – isn’t enough. There would have to be a worldwide monotonic decline in every field (including sports and art) from Athens to the present day. Only Explanation 3 holds water.
I brought this up at the conference, and somebody reasonably objected – doesn’t that mean science will stagnate soon? After all, we can’t keep feeding it an exponentially increasing number of researchers forever. If nothing else stops us, then at some point, 100% (or the highest plausible amount) of the human population will be researchers, we can only increase as fast as population growth, and then the scientific enterprise collapses.
I answered that the Gods Of Straight Lines are more powerful than the Gods Of The Copybook Headings, so if you try to use common sense on this problem you will fail.
Imagine being a futurist in 1970 presented with Moore’s Law. You scoff: “If this were to continue only 20 more years, it would mean a million transistors on a single chip! You would be able to fit an entire supercomputer in a shoebox!” But common sense was wrong and the trendline was right.
“If this were to continue only 40 more years, it would mean ten billion transistors per chip! You would need more transistors on a single chip than there are humans in the world! You could have computers more powerful than any today, that are too small to even see with the naked eye! You would have transistors with like a double-digit number of atoms!” But common sense was wrong and the trendline was right.
Or imagine being a futurist in ancient Greece presented with world GDP doubling time. Take the trend seriously, and in two thousand years, the future would be fifty thousand times richer. Every man would live better than the Shah of Persia! There would have to be so many people in the world you would need to tile entire countries with cityscape, or build structures higher than the hills just to house all of them. Just to sustain itself, the world would need transportation networks orders of magnitude faster than the fastest horse. But common sense was wrong and the trendline was right.
I’m not saying that no trendline has ever changed. Moore’s Law seems to be legitimately slowing down these days. The Dark Ages shifted every macrohistorical indicator for the worse, and the Industrial Revolution shifted every macrohistorical indicator for the better. Any of these sorts of things could happen again, easily. I’m just saying that “Oh, that exponential trend can’t possibly continue” has a really bad track record. I do not understand the Gods Of Straight Lines, and honestly they creep me out. But I would not want to bet against them.
Grace et al’s survey of AI researchers show they predict that AIs will start being able to do science in about thirty years, and will exceed the productivity of human researchers in every field shortly afterwards. Suddenly “there aren’t enough humans in the entire world to do the amount of research necessary to continue this trend line” stops sounding so compelling.
At the end of the conference, the moderator asked how many people thought that it was possible for a concerted effort by ourselves and our institutions to “fix” the “problem” indicated by BJRW’s trends. Almost the entire room raised their hands. Everyone there was smarter and more prestigious than I was (also richer, and in many cases way more attractive), but with all due respect I worry they are insane. This is kind of how I imagine their worldview looking:
I realize I’m being fatalistic here. Doesn’t my position imply that the scientists at Intel should give up and let the Gods Of Straight Lines do the work? Or at least that the head of the National Academy of Sciences should do something like that? That Francis Bacon was wasting his time by inventing the scientific method, and Fred Terman was wasting his time by organizing Silicon Valley? Or perhaps that the Gods Of Straight Lines were acting through Bacon and Terman, and they had no choice in their actions? How do we know that the Gods aren’t acting through our conference? Or that our studying these things isn’t the only thing that keeps the straight lines going?
I don’t know. I can think of some interesting models – one made up of a thousand random coin flips a year has some nice qualities – but I don’t know.
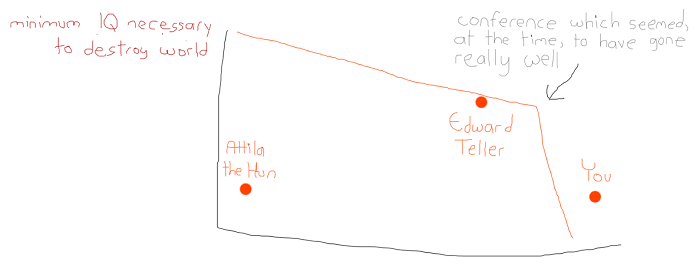
I do know you should be careful what you wish for. If you “solved” this “problem” in classical Athens, Attila the Hun would have had nukes. Remember Yudkowsky’s Law of Mad Science: “Every eighteen months, the minimum IQ necessary to destroy the world drops by one point.” Do you really want to make that number ten points? A hundred? I am kind of okay with the function mapping number of researchers to output that we have right now, thank you very much.
















I think we are looking in large part at a combination of factors 1 and 3. When a field is in the early stages of development, competent careerists are still able to make relatively big discoveries with relatively little effort. My own field is historical linguistics, which is a “sit around looking at manuscripts and thinking about them” field, not a “build a massive gadget for a hundred million dollars to play with atoms” field– but I’ve noticed something similar. The discovery of the laryngeals in Indo-European, for example, was made by Ferdinand de Saussure when he was still an undergraduate, and was then triumphantly confirmed by the discovery of Hittite twenty years later. Well into the 1960s and 1970s, you could still make relatively major-ish advances by simply writing five hundred pages on the development of the Tocharian noun, or ablaut in Slavic, or something like that–but now that that’s done the competent careerists have nothing left to do. My own specialty, such as it is, is in the historical linguistics of the families of North America, and there’s still a lot of work to be done–but the easy stuff is increasingly gone. Algonquian is the easiest family to analyze and it’s *mostly* been done to death. Siouan, Caddoan, Muskogean, etc. are a mess to work with. There is still lowish-hanging fruit available, but you have to be very dedicated and quite smart–in other words, not just a competent careerist. (Though maybe I’m just overestimating the extent to which people would want to spend months and months thumbing through dictionaries. Historical linguistics tends to attract a…certain type of person.)
I wonder to what extent this applies in other fields. Certainly, “save my own piss in bottles until it starts glowing mysteriously” is competent-careerist level of chemical research, not necessarily “one-in-a-billion genius” level. But it’s no longer possible to discover element 119 as a side effect of playing way too much Call of Duty in your basement.
A corollary of this is that the brilliant scientists of ages past may not necessarily have been as brilliant as even the average postdoc of the present day; they just had much more terra incognita to explore.
Humans may discover asymptotic limits to all that we are physically capable of comprehending. It’s no more reasonable to imagine the human mind can understand everything than it is to imagine the human stomach can digest everything — or that human muscles can lift everything. Once we’ve begun to max out our collective genetic potential in any given direction, the adaptation curve will flatten out. Impressive results will become fewer, and farther between. At this point, transhumanism becomes increasingly reasonable. The good news is: humans might actually get within spitting distance of peak attainable knowledge in the foreseeable future. That’s also the bad news….
You are starting to see papers with tens of authors in physics and now in genetics. There are very few single author scientific papers anymore in the natural sciences. Teams have firmly taken over. I am firmly of the opinion that we are running up against the limits of human cognition. There is no reason for us to believe that a 3 pound clump of cells can understand any level of complexity in the universe.
Another explanation could be that various fields like physics and biology have become sufficiently “deep” that you have to start specializing early on. Someone can dive into Evolutionary Theory, have the field stall on them, and not be able to make the transition to Bioinformatics, for example. There used to be Polymaths, able to push boundaries in 2 or 3 unrelated fields, but there are almost none now. Physics may now be big enough that it is difficult for a scientist to jump from one branch of it to another.
Analog May 1961 had an article “Science Fiction is too Conservative” where the author demonstrated that if you follow trend lines, we should be able to travel faster than light by the 1990’s or so. The article was reprinted in a number of places.
We were not able to travel faster than light by the 1990’s.
To think about it, max human travel speed achieved seems to be a rather weird metric which has been growing extremely fast for ~130 years from 1840s till 1968, but remained absolutely constant before and after that.
I think this post puts too little effort into interpreting the exact meaning of the progressions being graphed. A lot of the technologies shown to have linear progression here actually have faster progression than you are suggesting.
At high velocities, vehicle speed is largely dependant upon the non-linear effect of drag. Power requirements can be approximated as the cube of velocity. The increase from ~150 to ~400kmh on that chart for cars is a linear increase in velocity, but by plotting velocity you hide an exponential increase in power requirements. A 2.7 times increase in velocity is approximately a 19 times increase in power.
The same effect applies to a lesser extent to marathon speeds. A 1 hour marathon speed would require far more than double the effort of a 2 hour marathon speed.
As for agriculture, again the nature of the problem must be considered. There is a physical limit – the point at which 100% of the sunlight hitting an area gets converted into yield. In practice we are far off from this example, but consider a solar panel that has 98% efficiency vs that with 99% efficiency. It looks like a small increase, but another way of looking at this is a 50% decrease in losses.
If anything these graphs tell us more about the underlying nature of the problem than they do about any increase or decrease in the rate of technological progress on it.
I think the “low-hanging fruit” explanation is correct, but incomplete. Yes, most of the low-hanging fruit have already been picked; but the reason for this is that we’re running up against the limitations of fundamental physical laws.
For example, you cannot scale down transistors ad infinitum. At some point, electron tunneling will overwhelm your useful signal, and AFAIK we’re at that point now. This means that the next increase in computer speed per volume will have to be due to a qualitative shift — away from transistors, and toward something else (quantum computing, perhaps).
Similarly, ground vehicle speed is limited by all kinds of factors, such as the strength of materials the vehicle is made of, the power of the engine, and of course the driver’s reaction speed. Breaking the sound barrier is certainly going to be quite tough (outside of a few experimental racing vehicles). Moreover, there doesn’t seem to be much point in making consumer-grade cars faster until there are roads that can contain them, and drivers to drive them. Once again, we might be looking at a qualitative shift, toward AI-driven flying cars or some such.
We could probably keep improving crop yields for some time, but ultimately, conventional photosynthesis can only be so efficient. We could probably improve yields substantially through hydroponics in CO2-rich environments (which is already a qualitative shift); but ultimately, we’d need to invent some other kind of chemical/nanotech synthesis if we want to break through to the next level of productivity.
I’m going to comment in detail on the last paragraph, seeing as I’ve spoken out against that kind of neo-Luddite mindset before. I’d just like to point out that science has been advancing exponentially for quite some time, yet the world is still here. Also, if you’d like to walk on Mars one day, you’re going to need all the qualitative shifts that you can get.
Even when I clock in at 5 comments, someone has already said what I wanted to. I like this comment section; it saves me a lot of typing.
Small technical note – size of commercial transistors is still at this point limited by the wavelength of light used – it’s still visible light. I don’t wish to downplay the importance of material properties or tunneling current by any means, but there is a large amount of experimental effort in making the jump from vis to extreme ultraviolet at the moment, which suggests that the fundamental limits lie beyond our current capability.
(This may of course be different from the limits of scientific experiments, where tunneling current may indeed be the limiting factor. I’m not as familiar with that work)
Er, I meant, “I’m NOT going to comment in detail…”. Duh.
I studied English Renaissance lit in college, focusing on Shakespearean lit. Shakespeare was in fact amazing and brilliant and it also wouldn’t at all surprise me if there were in fact a hundred living English-language writers just as good as Shakespeare working right now. I think a lot of them are probably writing for TV and responsible for the new golden age of television.
I also think this makes sense if hypothesis #3 is true — it doesn’t get progressively harder to make great art because someone else made a bunch of great art first. There is no “low hanging fruit” to pick when it comes to artistic creation.
First of all, let me make a case for (3) being inevitable, and then let me explain why this doesn’t matter.
Diminished returns on transistor science are inevitable. There are a finite number of combinations of atoms which are improvements over our current transistor designs, and which are accessible to current technology, and which can be modeled by current theories and techniques. Finding those combinations is going to require increasing amounts of resources as transistors become more and more optimized, and the theory and techniques cannot help but become more byzantine.
However … how many of those researchers are involved primarily in the search space for shrinking transistors? The applications of transistors have also increased exponentially, and while maintaining Moore’s law is the field’s top goal, researchers who end up on a side-quest are not going to throw out their work, and will end up publishing transistor designs which contribute to other ways in which Transistors Take Over the World, be it noise-tolerance, corrosion-resistance, or biodegradability. Much researcher time is wasted, but probably an order of magnitude less than if the only metric considered is “scientific progress”.
Note that, in fields outside of transistors, “semiconductor research” is still booming, with lots of relatively low-hanging fruit. In the past 20 years, semiconductor research has grown to encompass LEDs, CCDs, CMOSes, avalanche photodiodes, solar cells, phased radar, lidar, laser diodes, gyroscopes, myriad bespoke chemical sensors, and even TVs (quantum dots are also called semiconductor nanocrystals). The number of applications of semiconductors is still increasing, even as the number of researchers in the field is limited to exponential growth by the number of PhD advisors. Even in this expanded domain, the number of “interesting” combinations of atoms is still finite, and limited, so progress will inevitably slow, but it will probably remain interesting for the rest of my career.
Conflict of interest statement: I have coauthored papers concerning the biomedical applications of some semiconducting materials.
Did you make the labels on those graphs with a mouse? They’re remarkably legible, if so! Bravo.
In a perverse kind of way, this article makes me feel better about my career accomplishments as a researcher : )
This seems obviously true. It reminds me of psychohistory from Asimov’s Foundation novels crossed with your own short story Ars Longa, Vita Brevis. Each individual person may have choice in their actions, but in the collective they are atoms bouncing around in an ideal gas that can be characterized by PV=nRT. The straight lines are created by the summing up of countervailing forces. On the one hand, you have human beings getting better at things, and getting better at getting better at things, and getting better at getting better at getting better at things exponentially, because that’s how humans predictably behave in the aggregate. Balancing that, you have a depletion of the fruit, which causes it to hang exponentially higher and higher. Put those two things together, and you reach neither takeoff nor stagnation.
At least until you run out of fruit altogether.
Is the last graph intended to help move more anti-anxiety supplement kits?
I think art and science are entirely different here, and I’ll claim that we have thousands of Shakespeares today. Painters like Rembrandt and da Vinci were geniuses and fantastic for their time, but today they would be unremarkable hobby painters unless they upped their game. They broke a lot of new ground in their time, but that ground is now broken for everyone.
The music of today, the story telling in movies and TV, the brand new art forms of computer games etc, all fed by a world wide connected culture, intense specialization etc, is vastly superior to the past, and quickly getting better. Is that even controversial?
The other addition to this: a greater percentage of the population are able to invest time into creating art, than in Shakespeare’s time.
Combine that with a larger population = more Shakespeares!
I will grant you computer games, seeing as it’s an entirely new medium; but how do you determine whether modern music and storytelling is better than the ancient kind ? Arguably, modern music is more repetitive than it used to be, but even so, aesthetic judgements are difficult to quantify.
Bravo.
It appears the researchers have rediscovered the law of Diminishing Returns.
Great post. Would have liked to see more discussion including the following two concepts:
1. Diminishing returns. This is similar to situation #1, but includes more complexities, such as the how need to publish overrides good scientific practices, so we end up having to redo a lot of research. More people in the system probably just makes things more crowded, and we should consider whether research dollars are getting diminishing returns. The graphs sure make it look that way.
2. S-shaped graphs for finite systems. Any finite system that appears exponential should eventually produce an S-shape, where exponential growth begins tapering over time. Is scientific understanding finite or infinite? Seems like it should eventually be finite to me, but perhaps we’re still too far away from the limits of knowledge to exit exponential growth. Meanwhile perhaps in isolated fields that see lots of research attention we’re reaching the limits of discoverable content? There are some crazy weird amino acids yet to be discovered probably, but most life on Earth is the ones we figured out long ago. Maybe we need to go into different fields in order to make progress in older fields, and that takes more time?
> All of these lines of evidence lead me to the same conclusion: constant growth rates in response to exponentially increasing inputs is the null hypothesis.
Doesn’t it also explains the cost disease in education and health?
One thing that surprised me about this article, because I take Scott’s take on issues like this very seriously, is the discussion of going with extrapolations from current trendlines. I had been under the vague impression for many years that this was one of the most common errors of prediction. At a certain point everyone was wringing their hands about the productivity differential between the Soviet Union and the United States. If you extrapolated from then-current trendlines, the USSR would overtake the US shockingly quickly. But the line didn’t hold. Every few years there was another scare brought about by naively assuming that current trendlines would continue. “Look at the Japanese economy’s growth!”, people said in the 1980s. “There must be something inherently beneficial about the way the Japanese economy is structured!” Then the line changed and everyone stopped talking about Japan and moved on to the next extrapolation from then-current trendlines. I thought that if you looked at old predictions, a very typical error involved assuming that then-current trends would continue, which almost always ends up looking foolish a few decades thereafter. Most predictions from a hundred years ago look like they took that world and extrapolated continuations of then-current trends, and were almost always wrong. The “future” of the 1950s was assumed to focus heavily on huge increases in space travel and space technology, in keeping with then-recent trends and this turned out to miss far bigger changes in areas that didn’t happen to be reflected in what had been going on around that time.
I realize this is all vague and fuzzy, and maybe I’m over-reading Scott’s discussion of expecting past trends to continue. None of this goes to the central issue of scientific progress that is the core issue of the post. But it surprised me enough to note this reaction. Am I reading part of the post correctly to say that, as a general matter, we ought to look at charts of past trends and expect them to extrapolate indefinitely into the future (recognizing that there are exceptions and we may be wrong)? And, if so, is that really right?
It seems to me like a lot of those cases are extrapolating from a deviation in the long-term trendline, which is the opposite of what Scott seems to be talking about. People in the 1980s were looking at the Japanese economic growth in the 1980s and expecting that current growth to continue, when what they really should have been doing was looking at Japanese economic growth since Japan was founded by Amaterasu. If they took the long view in this way, they would have been able to predict that the current growth was just a brief aberration from the iron trendline.
Your question sounds a bit like “How do we reliably predict global changes decades into the future?”, and the answer to this one, both from yours and Scott’s examples seems to be – well, we mostly don’t.
My impression is that the major point Scott was trying to make with exponential trends is that they can sometimes continue way beyond what you’d call impossible, and therefore you can’t use “But it’s impossible for this trend to continue that far” as an argument.
> This is the standard presentation of Moore’s Law – the number of transistors you can fit on a chip doubles about every two years (eg grows by 35% per year). This is usually presented as an amazing example of modern science getting things right, and no wonder – it means you can go from a few thousand transistors per chip in 1971 to many million today, with the corresponding increase in computing power.
Funnily enough, moore’s law is becoming increasingly difficult to perpetuate. We are approaching sub-nm pitch, and there is a fundamental lower bound to our current processes, at the very least at one atom of silicon, but likely a bit larger than that. Continuing exponential growth here means transitioning to a completely different technology altogether. While this is not impossible, such a transition would take monumentally more effort than any process change we have ever done before. I suspect there will be no exponential growth after around 2025, and continuing until we have a smaller process (if there is one).
“Constant growth rates in response to exponentially increasing inputs” is only looking at part of the elephant.
Nature happens in sigmoids, not exponentials. They stay near zero until something starts happening, then they take off in something very much like an exponential, but then the process reverses as physical limits kick in and you asymptotically approach saturation forever after.
Your graphs all start when things had already started moving, and don’t include the things that already hit their limits. So you’re just showing a bunch of snapshots of the initial takeoff part of the sigmoid.
This process is noisy and imperfect, so at the beginning of the slope it’s sometimes hard to predict where the limit will be (although I think we already knew the size of a silicon atom when silicon transistors came along), and thus growth can continue long past what people expect. But that doesn’t mean those things grow forever. They just flatten out and become part of the landscape of things we take for granted.
Maybe people can come up with better examples, but here’s an attempt at some technologies that have already saturated. And sure, you can be clever and say “why just campfires? That’s just a subset of ‘warming things up’, and now we have supercolliders that…”, but then you just keep going until it’s all part of the grand tapestry of human progress and now we’re just arguing about GDP growth again.
Campfires: millions of years of proto-humans can’t control fire. Rapid growth phase is when people figured out tinder and bow drills and so forth. Later we get matches and now we have fancy firestarters, but the basic notion of “collect some fuel and get a fire going, starting with tinder and building up to bigger logs” hasn’t changed in millenia.
Chairs: somebody sits on a log. Then somebody puts a fur skin down first. Once people settle down into villages we get furniture, four legged chairs are discovered and things take off a bit more. Today you can have more padding or wheels, but your Aeron is still basically a thing with butt and back support and maybe armrests.
Spoken language: Grunts give way to proto-language. Rapid growth as effective languages emerge and spread. Eventually we get modern languages, and now people invent Lojban and Esperanto and Klingon, but the remaining gains aren’t really worth anyone’s time for them to take off.
Travel by horseback. This one is more punctuated as we get saddles and bridles and stirrups. Horses are gradually bred to be faster throughout this period. But Kentucky Derby times aren’t going to halve again until we get our transequestrianist utopia.
Here’s a graph of transistor size showing a nice sigmoid shape.
Or consider the discovery of phosphorous you mentioned. Somebody notices it’s there, then we learn a bunch about it and a bunch of uses are found, and now we can still learn more about atoms in general, but we’re not still throwing exponentially increasing numbers of scientists at the study of phosphorous itself.
So yeah, as an important discovery takes off you’ll get exponential increases in the people taking an interest, and that growth will continue for a while as you start to max out, giving your “Constant growth rates in response to exponentially increasing inputs” effect.
But then it catches up, people accept the thing in its finished state and we stop thinking about it as a discovery at all.
There is a standard model that the log price falls linearly with log of the amount produced. Whereas BJRW seem to say that it should fall with the log of amount spent on production. Nintil cites Nagy et al, and I think they also go with the latter. But maybe the distinction between these two models isn’t so important.
One question is why these log-log phenomena happen, but another question is why this breaks down in the 70s for some industries. (graph)
An upbeat variant on this hypothesis is that if you’re reasonably excellent at something now, you could probably have made it into the history books had you been born in the right time.
Wikipedia has a list of ancient Greeks which numbers around a thousand notable people; based on some random clicking of names on the list, say 50% of those are from Athens, which a quick Googling suggests had a free population of around 20,000 in the circa 300BC range. Take a timespan of ~300 years for the intellectual heyday of the civilization, say lifespan of 30 years, that’s 1/400 level achievement to have your legacy persist for millennia (even better if you allow yourself to make it to adulthood). If you’d be the best in a decent-sized high school at something, you might have scholars of the field reading your work for ages or have changed the course of battles that brought down empires; if you got 11ish on the AIME, you might have been Euclid.
Another questionable assumption is that all researchers are actually working towards increasing the measured number. There are many other, harder to measure, qualities in these fields (eg processor architecture, bug resistance) that are investigated by these additional researchers.
#1 as stated strikes me as being incredibly thoughtless. If someone can point me to the “competent careerist” pathway to a tenured faculty position or equivalent (as opposed to the #2-ish grind of years of grueling underpaid PhD and postdoc positions and whatnot), I’d be much obliged.