I just got my exam results, so let’s talk medical residency standardized test statistics. In particular, let’s talk about average results by year – that is, compare doctors in their first year of training, their second year of training, etc.
I found three datasets. One is for internal medicine residents over their three-year education. Another is for psychiatry residents over their four-year education. The last is for surgery residents over their five-year education. All of them are standardized to a mean of 500 and standard deviation of 100 for all years lumped together. Here’s how they look:
INTERNAL MEDICINE (numbers eyeballed from graph)
Y1: 425
Y2: 500
Y3: 550
PSYCHIATRY
Y1: 412
Y2: 485
Y3: 534
Y4: 547
SURGERY
Y1: 399
Y2: 493
Y3: 543
Y4: 565
Y5: 570
Year of education starts out as a relatively important factor relative to individual differences, but quickly becomes irrelevant. There’s only a 17% chance that a randomly chosen first-year surgeon will know more about surgery than an average second-year. But there’s a 31% chance a second-year will know more than a third-year, and a 48% chance that a fourth-year will know more than a fifth-year. Compare fourth-year and fifth-year surgeons, and it’s pretty close to 50-50 which of them will know more surgery.
(also, four percent of final-year surgeons about to graduate their training know less than a first-year trainee who just walked through the door. Enjoy thinking about that next time you get an operation)
It looks like people learn the most in their first year, and less every following year. Checking averages of all the programs together supports this:
Y1 – Y2: + 81 points
Y2 – Y3: + 50 points
Y3 – Y4: + 18 points
Y4 – Y5: + 5 points
The standardized nature of the scoring hides how minimal these gains are. The surgery exam report tells me the raw percent correct, which goes like this:
Y1: 62%
Y2: 70%
Y3: 75%
Y4: 76%
Y5: 77%
So these numbers eventually plateau. I don’t think any residency program has a sixth year, but if it did people probably wouldn’t learn very much in it. Why not?
Might it be a simple ceiling effect – ie there’s only so much medicine to learn, and once you learn it, you’re done? No. We see above that Y5 surgeons are only getting 76% of questions right, well below the test ceiling. My hard-copy score report give similar numbers for psychiatry. Also, individuals can do much better than yearly-averages. Some psychiatrists I know consistently score in the high 600s / low 700s every year. Why can’t more years of education bring final-year residents closer to these high performers?
Might it be that final-year residents stop caring – the medical equivalent of senioritis? No. Score change per year seems similar across residencies regardless of how long the residencies are. For example, internal medicine residents gain 50 points in Year 3, about the same as psychiatrists and surgeons, even though internists finish that year, psychiatrists have one year left to go, and surgeons have two.
Might it be that programs stop teaching residents after three years or so, and they just focus on treating patients and not learning? That hasn’t been my experience. In my own residency program, every year attends the same number of hours of lectures per week and gets assigned the same number of papers and presentations. I think this is pretty typical.
Might it be that residents only learn by seeing patients, and there’s only a certain number of kinds of patients that you see regularly in an average hospital, so once you learn the kinds of cases you see, you’re done? And then more book learning doesn’t help at all? I think this is getting close, but it can’t be the right answer. If you look at that surgery table again, you see relatively similar trajectories for the sorts of things you learn by seeing patients (“Patient Care”, “Clinical Management”) and the sorts of things you learn from books and lectures (“Medical Knowledge, Applied Science”).
I don’t have a good answer for what’s going on. My gut feeling is that knowledge involves trees of complex facts branching off from personal experience and things that are constantly reinforced. Depending on an individual’s intelligence and interest in the topic, those trees can reach different depths before collapsing on themselves.
Spaced repetition programs like Anki talk about the forgetting curve, a model where memorized facts naturally decay after a certain amount of time until you remind yourself of them, after which they start decaying again (more slowly), and so on until by your nth repetition you’ll remember it for years or even the rest of your life.
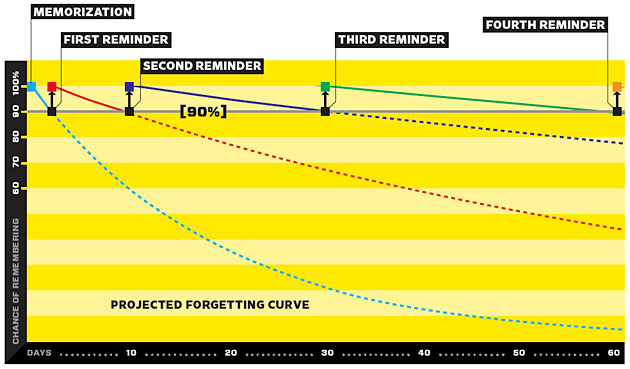
Most people don’t use spaced repetition software, at least not consistently. For them, they’ll remember only those facts that get reinforced naturally. This is certainly true of doctors. By a weird turn of fate I earned a degree in obstetrics in 2012; five years later my knowledge of the subject has dwindled to a vague feeling that this comic isn’t completely accurate. On the other hand, I remember lots of facts about psychiatry and am optimistic about taking a board exam on the subject in September.
But most residents in a given specialty work about the same number of hours, see about the same sorts of patients – and yet still get very different scores on their exams. My guess is that individual differences in intelligence and interest affect things in two ways. First, some people probably have better memories than others, and can learn something if they go six months between reminders, whereas other people might forget it unless they get reminders every other month. Second, some people might be more intellectually curious than others, and so read a lot of journal articles that keep reminding them of things – whereas other people only think about them when it’s vital to the care of a patient they have right in front of them.
This still doesn’t feel right to me; I remember some things I’m not sure I ever get reminded about. Probably the degree to which you find something interesting matters a lot. And maybe there’s also a network effect, where when you think about any antidepressant (for example), it slightly reinforces and acts as a reminder about all your antidepressant-related knowledge, so that the degree to which everything you know is well-integrated and acts as a coherent whole matters a lot too.
Eventually you get to an equilibrium, where the amount of new knowledge you’re learning each day is the same as the amount of old knowledge you’re forgetting – and that’s your exam score. And maybe in medicine, given the amount of patient care and studying the average resident does each day, that takes three years or so.
Why does this matter? A while ago I looked at standardized test scores for schoolchildren by year, eg 1st-graders and 2nd-graders taking the same standardized test. The second-graders did noticeably better than the first graders; obviously 12th graders would do better still. But this unfairly combines the effects of extra education with the effects of an extra year of development. A twelfth-grader’s brain is more mature than a first-grader’s. Louis Benezet experimented with teaching children no math until seventh grade, after which it took only a few months’ instruction to get them to perform at a seventh grade level. It would sure be awkward if that was how everything worked.
Medical residency exams avoid this problem by testing doctors with (one hopes) fully mature brains. They find diminishing returns after only a few years. How much relevance does this have to ordinary education? I’m not sure.
















What fraction of residents drop out during each year? Could these results be explained if lots of the lowest-scoring students drop out after the 1st year, a few low-scoring students drop out the 2nd year, and by the end of the program nearly everyone sticks around? Maybe residents learn more each year but gains in the mean score exhibit diminishing returns because the pool of students taking the exam changes most in the early years of a program.
I think low dropout rates in psychiatry and medicine. In surgery there’s this weird thing with a transitional year, where a lot of people (generally not as smart as the actual surgeons) take the first year of surgery residency and then do something else. I’m not sure if they take the test or how that affects the test scores. There’s also a weird thing where some psychiatrists leave after third year to do child, but I don’t think they’re any smarter or dumber than the others.
That would make it worse, wouldn’t it? If the pattern in test scores is explained by low-scoring students dropping out, high scoring students could be not gaining at all!
Yes; when taken to its extreme, it would imply that good students are stagnant, and all the gains come from bad people dropping out.
Dropouts were my first thought as well. Even if the dropout rates are low, removing outliers can change the mean pretty dramatically.
How good is the gaussian approximation for these tests? I would expect it to be rather bad, so the calculations involving the tails of cumulative functions (e.g. probability of a 5th year knowing less than a 1st year) could be off by a lot. I feel like a lot of these changes in mean might be better explained by changes in score distribution over the residency period.
Residency usually runs from, what, ages 25-30? Lots of stress, poor sleep, poor nutrition? Could be we’re dealing with the opposite of the extra year of development. Just a thought.
More like 30-34… These days, gap years before entering medical school (do to research, work in pharma, etc) is all too common.
My guess is that the smartest people are going to get an A in the class anyway, and the dumbest people are going to fail the class anyway (barring stringent entry requirements). The class teaches just enough to get the middle-tier students up to par, but once you reach a certain cap on how much information they can retain, the benefit by taking more classes is offset. Did you look at the median scores in those categories? I’d predict that the residents in the IQR are showing the most growth, whereas the upper and lower quartiles don’t change in range too much.
EDIT: For residency, it’s the same idea. Places meant to educate people invite all types, but not everyone is able to meet those standards.
“Louis Benezet experimented with teaching children no math until seventh grade, after which it took only a few months’ instruction to get them to perform at a seventh grade level. ”
My kids were for some years in a school modeled on Sudbury Valley–in school unschooling. At one point some of the students asked a staff member to teach them math. It was a mixed group, starting with nothing. In a year they were learning algebra.
How old were they?
Don’t know about mr Friedmans kids, but I have some experience with premature children who are kept out of school because they need to learn other stuff, like basic motor skills/neuromuscular training. (similar to tiny stroke patients really)
They typically start school directly in 3rd or 4th grade and are caught up within a year or so. I think people around here have mostly agreed that the first 3-5 years of school is just storage for kids.
They could make it something useful, of course, even with the effect given. There are less book knowledge based skills, like social interaction or physical dexterity. Ie spend more time playing out and about.
Indeed and they probably should. When I first got involved with the premature kids, I read a bunch of articles that seemed to find that kids who play outside a lot end up smarter than sedentary kids because of increased blood flow to the brain while it’s developing. If this has been reproduced, it’s even more stupid to force the kids to sit inside.
The problem seems to be that politicians seem hopelessly stuck in “Moar maths in first grade!!1!!1!” mode.
I blame star trek (A throw away line in one episode about a 9 year old not doing his calculus homework)
Some academic subjects are learned more easily at younger ages, though, like second languages. Unfortunately, we seem to have decided to introduce math in first grade and foreign language classes in high school.
By what landmarks I can pull together, I would have been no older than 11, probably no younger than 9. There were three other kids in the class: one extremely socially-adept and academically anti-adept girl who was a year or two older than me, one girl my age who was probably Gifted*, and one girl two or three years younger who was also quite bright, though I didn’t know her very well. We started with addition and subtraction, though I at least already knew those (my actual knowledge limit was multiplying multi-digit numbers, though, which in my defense I had never had to think about before, so I wasn’t way ahead) and ended with basic algebra and geometry – you know, two equations and two unknowns, area and diameter and pi. It was fun. So far as I could tell – and we were all doing problems in class, so it was fairly obvious – everyone was following just fine. Sadly the class broke up after one year, and I had to do all further math on my own, which was much less fun.
*Everyone at a Sudbury school, so far as I can tell from personal experience, is either Gifted, Special Needs, or occasionally both. If the schools aren’t failing kids, they don’t end up at a Sudbury school, and those are the two groups they tend to fail in ways that cause parents to look for something different.
What’s the incentive structure for these tests like? Maybe upper year residents have just learned to beat the minimum requirement and have no further motivation to achieve scores higher than that?
I know I’m unreasonably (in terms of how risky it was) proud of fulfilling a mandatory requirement in university with about half a percent above the cutoff, minimizing the work I put into it. The thinking might be similar for upper years?
It varies by residency. In some residencies you can get “put on probation” or have to take remedial classes if you don’t do well enough. In others it doesn’t matter. My residency tells first-years not to study so that they look better (the program looks better?) when they do much better second-year, but I don’t know how common this is.
Scott – my girlfriend is a psych resident. Haven’t you heard the mantra: Step 1: 2 months, Step 2: 2 weeks, Step 3: number 2 pencil.
I was the same way back in undergrad — always aiming to minimize effort by skirting whatever ceiling a given assessment happened to have (e.g. no use getting all the questions right if 1600 or w/e is the highest # of points they’ll give you). My final accomplishment in that regard was making it in just (~1-2%) above the cutoff for “summa cum laude”, which was the highest latin honor I could get and the only thing grade-related you’d leave on a resume/cv after graduation (not that anyone gaf ofc).
Probably not the best strategy but it’s worked ok for me so far.
Yes this: satisficing. This was a very common story in my experience of teaching: students have too much to do so will aim to get what they need, rather than the highest mark possible. Subsequent work in online education software indicated similar behaviour: they stop when they’re “good enough”.
Some countries’ education systems can buck this by rewarding top performers — I’m uncertain, but Spain might be one: the hospital you get into is determined by your final mark (I *think*). Would be interesting to see your numbers for other countries.
I don’t know how large the effect would be, but I’d guess at least some of the larger effects early are partly due to students learning about the test itself – the structure, good strategies, pacing, etc. – and getting more comfortable with it.
How is this not just expected diminishing returns? I’d be very surprised at anything approaching linear improvements in this setting. In most domains you get most benefits early.
For a bizarre parallel that may be less vacuous that it appears: for all dynamic bug finding methods, testing small numbers of things detects most of the bugs you find. After an initial spike, things tail off pretty consistently. Doesn’t matter the method. There’s another spike (smaller) in new bugs when you change the strategy (e.g., switch tools), but this next strategy will similarly bottom out quickly. Often N=1,2,3 (for whatever noun you care to count) gets you the most benefit. E.g., the bugs found with N=1,2 threads or N=1,2 inodes (if that’s your thing) swamps the bugs found with N=1000.
I’d bet money that a similar thing is going on here. Weirdly.
Can we have links to further reading? I don’t doubt you, but it seems like an interesting read over the weekend.
Getting off topic, but this originates with real bugs and other wildlife: the Lincoln index estimates numbers of unobserved items on the basis of two independent observation sets, and the species discovery curve can be used to help identify a point of diminished returns when surveying wildlife in a particular environment — its applications range far wider though, including things like vocabulary estimation.
With regards to software bugs, these approaches can be problematic: here’s an example critique.
Thanks for the last link, that’s my weekend blown on one single blog methinks.
Just to be clear: the fact that you don’t find many more bugs with the tool(s) you use doesn’t imply that there aren’t a lot more left. It’s just that given a dynamic strategy X, it often hits diminishing returns quickly.
This comment suffers from being written/minorly revised out-of-sequence. Enjoy!
Test scores plateau because these are norm-referenced tests; the average score is (approximately) 500 by definition (or, if you prefer, by design). Once everyone’s exposed to the material the test covers, it turns into an IQ test.
Suppose we closed one of these specialties, so no one was allowed to come in to the specialty. For the sake of the example, we’ll keep testing everyone every year until the end of time. Immediately after we close entry, the mean score every year will be 500, because it’s 500 by definition. Once everyone currently in the training pipeline has made it all the way through the pipeline, they’ll know a little more, and the mean score will still be 500, because, by definition, it is 500. No amount of training, experience, or knowledge, however measured, can ever affect the mean score on the test. It can affect the raw score (“raw percent correct”, in the terms of the post), but not the normed score.
So the fact that Y1 students have a mean score below 500 is an artifact of the fact that they, as a group, do badly on the test compared to everyone else. That is caused by their lack of exposure to the material and is easy to solve — expose them to the material! That makes for a quick jump in scores. The residual difference, where some of them absorb the material and subsequently get higher scores, while others don’t and don’t, is not caused by lack of exposure, it’s caused by their individual qualities, and can’t be solved.
This is an odd conclusion to draw, because you have no way of measuring “amounts” of learning. What unit of learning are you using? If a doctor devotes their life to an in-depth study of the pituitary gland and conditions affecting or affected by the pituitary gland, how “much” do you intuitively feel they might learn over 40 years, and how much of that would any of these standardized tests allow them to display? If your answer to the second question is less than your answer to the first, that is sufficient for raw scores to plateau.
This is also a strange point, in that if Y5 surgeons were getting 100% of the questions right (on average!), the test ceiling would be raised. The test is a measurement tool that we use to measure residents, not a rite of passage ordained by God. If the ceiling is so low that the average (!) raw score is 100%, we’re not getting any information from our assessment tool.
The way I’d think about this is “the surgery test defines a curriculum we’d like surgeons to be familiar with. The learning curve for this curriculum appears to justify about three years of training.” After those three years, basically everyone has had as much exposure to that curriculum as they’re able to profit from, and you’re left with a residual IQ test.
You could trivially design a test that saw a much longer time to plateau by including more material in the curriculum implicitly defined by the test. But what would be the point? That’s just saying “we want to have an educational period that lasts 20 years, and we’ll cram stuff in there, no matter what it is, until it takes 20 years to learn it all.”
My preferred explanation too.
I’ll add though that studying is not simply a bit transfer between a page and a brain: to understand something, you need to connect new bits of information to things you already know, work with the new bits and connect those to concrete experience.
This means that even if the accumulation of knowledge might be linear, studying is really exponential: it is possible that those first three years represents the linear region of the exponential, after which the knowledge web becomes too complex to be expanded at a constant rate.
I’m confused.
Imagine that the test scores went:
Y1: 400
Y2: 450
Y3: 500
Y4: 550
Y5: 600
This would fit the standardization (mean of 500, etc), but would show everybody improving at the same rate (ie without plateau). Don’t we need another explanation for why 3rd and 4th years stop improving?
Also, see the raw percent scores, which show the same pattern.
I’m not complaining that the ceiling for surgeons is less than 100%. I’m saying that we can’t say the reason surgeons stop improving is because they hit a 100% ceiling, because they didn’t.
You explain this as “after those three years, basically everyone has had as much exposure to that curriculum as they’re able to profit from”, but that’s exactly the mysterious phenomenon I’m trying to unpack. What does it mean to say that the curriculum inherently takes three years to learn, when everyone has learned a different amount of it after three years?
This explanation was my working hypothesis reading the post too.
By this explanation, 3rd and 4th years stop improving because it’s harder to teach them things that will make them better at the tests. Pretend there are four questions:
1) What is the singular of “data”
2) Explain cellular respiration
3) Explain the Dark Cycle
4) Diagnose a patient with the following symptoms. Discuss alternative diagnoses and why you discounted them, as well as any follow-up questions you would ask.
The amount of education it takes to teach someone to get the first question right is approximately zero. The amount of education it takes to teach someone to get the second question right is small. The amount of education it takes to teach someone to get the third question right is moderately sizable. The amount of education it takes to teach someone to get the last question right is a lot.
In one year, you can teach someone how to answer a lot of questions like the first and the second, but only a few questions like the third or the fourth. So the first year students learn how to answer lots of questions they previously couldn’t, while the fifth year students learn to answer only the hardest questions, that take longer to learn how to answer and have more uncertainty even for a well informed person.
The fact that it’s a weighted test seems important, but really the crux here is that learning deeper about a subject is a process that experiences diminishing marginal returns when measured in “number of questions you can answer”
Let’s not overlook that “number of questions you can answer” is an inherently worthless metric (that’s why we norm the tests!). We could add another question to your test, “what is the plural of ‘museum’?”. We’d probably see some improvement, after adding that question, on “number of questions you can answer”. For one thing, the high score would presumably increase from 4 to 5. But so what?
Well, no. The concept of “rate” here is not well defined, because, as I mentioned, the concept of “amount” is not well defined, and “rate” is amount per unit time. I think you’re making the mistake I mention at the very end of my earlier comment (“we could trivially create a longer learning curve by adding material to the test” [1]). You’re definitely making a mistake with respect to standardized scores; 50 points up from 500 represents a much larger improvement in raw % correct than 50 points up from 650 does. (Compare SAT scores — when I was a senior in high school, missing one math question knocked your score from 800 to 780. But the difference between 1000 overall and 1020 is many questions, not one question.)
We can say the reason they stop improving is that they hit a 100% ceiling. It is the ceiling of their ability to learn rather than that of the ability of the test to learn about them. Both of those are real things. You’ll always see a population hitting one or the other.
You’ll notice that I didn’t say “the curriculum inherently takes three years to learn.” I said “this curriculum appears to justify about three years of training.” That’s a purely empirical conclusion based on the observed average learning curve for the curriculum, which shows noticeable improvement for the first three years of study and zero improvement afterwards. (It’s quite possible that learning irrelevant to the test is taking place during the last two years. Obviously, that doesn’t show up on the test and is therefore not part of the curriculum defined by the test.)
How would you suggest assessing how long a curriculum takes to learn, other than by teaching it to people and seeing how long they take to learn it?
[1] I’ll give an example here of the kind of thing I’m talking about: imagine we’ve got a literature test based on To Kill a Mockingbird. People who have never heard of the book tend to do badly. Highly verbal people who have read the book many times do well. As an English class goes through the book, their scores on this test will tend to rise until they’ve read it, discussed it, and listened to what the teacher thinks they should believe about the book (or decided not to do those things). Then they’ll plateau. We could expand the test to cover Dracula as well as To Kill a Mockingbird. The new test has a bigger curriculum, and an English class, starting from nothing, will see training-based gains on it for a longer period than the class being tested solely on To Kill a Mockingbird. But then they’ll plateau. The longer learning curve doesn’t mean education in the two-books class is more effective, and it doesn’t mean the students are learning any more about To Kill a Mockingbird; it means the curriculum is larger.
Move past the idea “I want to see arithmetic progression in the scores from year to year.” The scores can be whatever we’d like them to be; we currently want them to be informative as to the quality of the students who take the tests. What reality do you want to see behind the scores? Have you never met anyone who couldn’t be made to understand something no matter how much time they spent on it? Under the current system, people like that get low scores. We could have a different system — what would be the benefit?
Its best to look at the test itself to see how loaded it is for fluid vs crystallized intelligence factors.
The spaced repetition curve and typical person motivation and personal interest could explain on platues for tests heavily loaded on crystallized intelligence. That *is* another form of intelligence, though, and a very important one. I suppose it can be somewhat located in 4th year senior GPA for classes that build on earlier ones.
The test itself will be able to reveal how much is due to raw fluid IQ loading, or differing rates of learning and forgetfulness.
It seems this is mostly a fact-based test, so I think Scott’s explanation works better then fluid-based loaded tests.
Each brain has limited size of its memory banks and its algorithms can’t change, so yes this eventually applies to every topic.
Maybe out of all the material on the tests there is around a 1/4 that is neither useful nor interesting and which therefore even people with a lot of experience have a hard time remembering
Waldorf schooling is basically placebo schooling (varies by country how placebo they are allowed to be), but Waldorf kids seem to do well in either high-school or college.
A few more potential explanations.
1) The numbers you are reporting seem to be entierly harvested from exams and other formal learning metrics. Such metrics are often heavily biased toward information that is easily regurgitatable and has clear definite answers. I suspect a great deal of what residents learn, especially later in their residency, is more squishy information like ‘If a patient presents with X, Y it works best to try W, Z first’ which (because it is only true ceterus parabus) is hard to accurately and fairly test for.
2) Tests are biased toward information that is uncontested and applicable to everyone. As residents knowledge catches up with the cutting edge the new information they learn is no longer so well established as to make it onto tests. Also, to the extent residents pursue greater specialization than the tests accommodate what they learn may also not be reflected, e.g., if one decides to focus specifically on opiate addiction treatment in the final year of residency you might be focused on pretty arcane facts about the operation of G-protein receptors, the difference in effects between mu kappa and (forgot third) receptors and the weird differences between opiates on G-protein recycling which is unlikely to be tested in any comparable fashion.
3) Often when learning a field it is important to learn many facts just for the purposes of understanding what you really need to know. For instance, in mathematics it’s often necessary to learn all sorts of boring bookkeeping facts/theorems when first learning a field to gain a proper understanding of the important theorems you learn latter but once you’ve done that there really is no need to remember the boring bookkeeping. I expect similar things are true in medicine and if so you aren’t really forgetting operationally important information.
I don’t know how it is in medicine, but in maths, unless you use something on a regular basis, you tend to forget it. You read a theorem, understand its proof completely but if you don’t put into to some use, you forget it very quickly (or more often you recall something rather vague). The trouble is that while the proof tells you why the particular statement is true, it does not really tell you why the statement is the way it is. Terence Tao writes about it on his blog – you should always try to do a lot more with the theorems. The first thing to do is to realize where in the proof you need all the conditions in the statement, which most people do, I guess. But another thing is to ask “why do I need this condition? Are there counterexamples where it won’t work? Are there ways to replace it with something so that I don’t need it in special cases? If I make some extra conditions, can I say something even stronger?”.
Most people, definitely most students, don’t do this. And so they don’t remember much afterwards, even if they can follow the proofs perfectly. Now, if you’re interested in something you do these things naturally. You might not remind yourself of a particular theorem, but you think about its implications and that is an even better way to remind yourself of it than simple re-reading is. So as long as it is at least a bit similar in medicine, I think the effect really is that you forget what you don’t use or remind yourself of in other ways.
Btw, another great way to learn things is to teach them. In the first 3 years of my PhD I did not have to teach any exercise classes but this winter semester I did and even though the course was fairly basic (introduction to stochastic processes, going from Markov chains to discrete time martingales) and I actually know a lot of it I still managed to learn a few new things (because students sometimes ask questions you have not thought about and even more importantly, they make mistakes you would not make and then you have to think about why this particular approach does not really work) and solidify what I knew already. Of course, it takes some of my time I could theoretically spend working on my thesis, but I still wish they had me do it earlier, because it really seems to be one of the best ways to learn things (IIRC, based on what he says, David Friedman seems to have learned a great deal of economics this way).
I’m very grateful to one of my professors who taught me that the first thing you should always do with a theorem is play with it. Identify where each assumption is used. Come up with a list of examples where the theory works. Come up with a list of examples that break at each step an assumption is used. I (a combinatorist) might not remember much analysis, but I can remember the important counter example functions (the cantor function, the Weierstrass function, e^(-x^2), etc) and use them as truth-testers for theorems.
Also, teaching is definitely the best way to learn things really well. One thing I’ve noticed is that there are often many ways to intuitively understand mathematics that aren’t taught in classes very often. I often learn these by teaching mathematics. One notable example was that I was teaching Taylor Polynomials and my students wanted to know why the radius of convergence is what it is. They understood they could use the ratio test to calculate it, but they wanted a good reason why it happened. A little poking around made me realize that the radius of convergence is the distance from the center to the nearest pole in the complex plane. My complex analysis class never bothered to tell me that, but I always tell it to people I’m teaching calculus too, because it makes a huge amount of sense.
Yeah, pictures and intuitive examples (if perhaps necessarily simplified) are often as important as proofs, sometimes more so, since some proofs are very technical and do not really give you neither much insight or new tools you could apply elsewhere.
I liked that I took the physics classes that required the math I was learning in math class at the same time, roughly.
Sometimes this was slightly consternating. But mostly it just helped the math make sense.
I’m fairly sure this is how everything works. Look at people who got their educations interrupted (or precluded) by World War II, and then got shortened, 1-2 year versions as adults. They didn’t come out half-educated morons, did they?
Another data point is unschooling, which relative to public schooling, leaves kids at one grade lower than expected. One grade!
Unschooled kids are hardly representative of the population as a whole. I’d bet they are on average pretty high-IQ. We should compare like with like: unschooled kids with public-schooled similar-IQ children.
Or, more relevantly: we’d need to randomly assign some below-100 IQ kids to be unschooled and see how well they do. My guess: not well.
My guess would be that they’d do one grade below their below-100 IQ peers.
I think the assumption in the question is that the data on unschooled students being on average 1 grade level lower than traditional school students doesn’t take into account the selection bias of unschooled kids.
So if you actually took kids at random and unschooled them, they might(probably would) perform worse than 1 grade level below traditional school students.
Possible. I would very much like to see studies of homeschooling and unschooling with controls for IQ. (It would go a long way towards deprogramming people from their prejudice against private tutoring.)
I wrote some long-winded thing here, but it wandered far afield, so I’ll just quote my old language testing prof: it’s not just the interactions, it’s their plasticity.
re:equilibrium
I think that holds a lot more for “lists of facts” type of knowledge than for other types.
Back in school I remember some subjects that were almost mindless learning of statements and facts and if you could regurgitate them then you got your high marks.
The “new knowledge you’re learning each day is the same as the amount of old knowledge you’re forgetting” holds in such cases.
but there’s also other types of knowledge. In math, programming and many areas of science there’s often a “click” moment where you reach a level of understanding of something where it suddenly all clicks into place and your mental model gets a major improvement and suddenly you don’t need to rote learn, you can now know things you’ve never been told about the subject.
The reason why a programming language behaves how it does clicks and suddenly you don’t need to retain lists of facts, you can re-derive them on demand.
The way RNA behaves how it does in some situation clicks and suddenly you don’t need to remember a load of special cases.
The logic of some branch of math clicks and suddenly you don’t need to remember all the little special cases because they all make sense.
Professions that focus on problem areas that tend to have that click moment, with systems that have clear underlying rules I don’t think are so limited by that equilibrium because very little knowledge needs to be retained.
Medicine seems big on lists of facts… probably because there’s so much about the human body where nobody anywhere understands enough of the underlying mechanisms involved which seems reasonable.
I had classmates who tried to apply the rote learning model to things like programming exams… they tended to have a bad time because they’d try to regurgitate memorized programs in exams meaning they had to memorize vast swathes of code perfectly when it took vastly vastly less mental effort to just understand the material and yielded better results.
(my first post: Hello everyone! If there are certain rules for newcomers, please let me know)
I’m not a doctor, so my experience is limited to once getting some kind of an education, but here are two theories:
1. Perhaps education involves learning the sort of things that can and cannot be measured by testing. In the later years, education starts focusing more on skills that aren’t captured on tests, resulting in an apparent plateau.
2. Signalling. New arrivals in an educational institution are starting from a blank slate, eager to define themselves to their peers/educators/recruiters/themselves. In the beginning, academic achievement is a good way to accomplish this. In later years, they become somewhat of a known quantity. Even when they encounter new peers/educators/recruiters their a known persona in the eyes of some peers (and themselves) and this is enough to communicate who they are to others.
I am a family medicine physician. At one point, I was working with a new sub-specialty and I got to help create their board exam. I suspect that the residency exams are created in a similar way to what I worked on.
The first thing we did was create a list of what we thought everyone in that sub-specialty should know. We each took topics we were interested in and we looked at the literature and then created exam questions based on that literature. (We tried to use literature from reliable, peer reviewed sources.) Then we tested the questions on the other members of the group and weeded out the bad questions. The last stage was testing the questions in an actual test situation and seeing how well they did.
We tried to arrange the test so there was a certain percentage of easy questions that everyone should be able to answer. We also wanted a certain percentage of very tough questions that we thought only a few people could answer. The rest of the questions were supposed to fit in the middle between the two extremes.
On each exam, there are always the questions that do not count towards that exam. They are being tested for future exams. The test maker will gauge how people answer the question and decide whether to keep it for a real exam question. The test maker thus has some idea how well the question will be answered.
When we were making the test we especially liked the questions that would be answered correctly by the people in the middle to high test score outcomes but not by the people with low scores. If there was a question that was answered correctly mostly by the people with final test scores on the low end (or people who failed the exam) but incorrectly by the high scorers, that question would be thrown out.
One point is that these tests are designed to have a certain number of questions that the majority of test takers won’t know the answer. It would be surprising and probably suspicious if someone scored close to 100%.
The other point is that the creation of these exams is a subjective effort and not as scientific as the companies would have you believe. I think that there are many ways an excellent physician can do poorly on these exams.
One problem I have seen is when literature has conflicting results. When I last took my board exam, I specifically remember one question that bothered me. It listed four possible answers. The problem was that I had read one study that concluded one of the answers was correct while there was a second study that supported a different answer. It became a test of “guess which study was used by the test maker”.
One factor that may also influence the residency test scores is that many of the questions are reused every year. So residents may have been exposed to the question in the previous year and may be more likely to get it right as they are repeatedly exposed to the the same or similar questions. Here’s a wild idea: what if all the improvement is just a result of becoming familiar with the questions and doesn’t represent learning at all?
Could you explain the reasoning behind this?
The point of tests is usually to tell test takers apart. Such a question is useless by that metric.
The test as described seems like it’s purpose is to determine a basic level of understanding, not necessarily to differentiate between test takers (like a driving test)?
Edit: I guess basic knowledge test are still differentiating between people who do or don’t have the basic knowledge.
My confusion I guess is why the question above would be useless in that context?
If I want to see if you have minimum understanding of a topic, is it obvious that questions that low performing students get right and high performing students get wrong, are negatively correlated with a minimum understanding of the topic?
It might mean, for example, that the question is written confusingly enough that people are misinterpreting it, and the people who misinterpret it and are smart all get it wrong, whereas the dumber people guess and a quarter of them get it right (assuming multiple choice).
Useless? That class of questions is literally defined by being informative. They distinguish low scorers from high scorers, just like all the other questions are supposed to.
There’s no rule that says getting a test question right has to increase your reported score.
The idea might be the the exam-takers probably get that question right based on false reasoning. You don’t want to reward that.
The worst case scenario is that the classes teach people the wrong thing. In that case, you also don’t want to reward people who didn’t learn the material (and together with tossing out the question, you’d want to improve the teaching).
I guess this covers some of what I got hung up on. Questions of the type in the quote seem like they would be very information rich, in terms of test design. It would seem to me that a test designer could learn more from a question of that form than they could from most other kinds of questions, and so the idea of just throwing out this, apparently very useful information, seemed strange to me.
This is standard practice in item analysis. Typically you’d use a point biserial correlation to find them. The reasoning is that items that high scorers perform poorly on and low scorers perform well on are likely to have that outcome because of poor wording, confused reasoning, or out-and-out incorrect answers (or a correct distractor). Anyway such a condition violates means of determining validity such as convergent validity. You couldn’t expect such a result on a test of a similar construct so you’re undermining the validity of the item.
I can certainly understand why it would be important to pay attention to and investigate questions like this. I think maybe I just constructed a hypothetical in my head that does not match to reality very often where in this kind of question reflects some kind of bias in reasoning that is potentially useful?
Essentially that there might be information that is important to test for but that does not correlate with a general understand or in this case is negatively correlated with a general understanding of the other material.
A hypothetical word problem that confuses the otherwise high performing technical students because it is based on a negatively correlated with technical expertise, social intelligence, which is still important for a doctor to have, or something?
That’s very well stated. And yeah, it could certainly happen! The problem is that, in real-world terms of test diagnostics and triangulating validity, it would be very very hard to establish disciplinary best practices and (legally defensible) quality standards that could screen out real problems with items from the kind of situation you’re describing. So you’re not wrong at all with your hypothetical – I’m sure it occasionally happens – but in the pragmatic sense of large-scale test development, particularly for high-stakes, high-scrutiny tests, it’s not something most developers would be comfortable with.
That seems perfectly reasonable!
Fulcher is good here: https://books.google.com/books?id=jbMuAgAAQBAJ&pg=PT190&lpg=PT190&dq=glenn+fulcher+point-biserial+correlation&source=bl&ots=n3NKDjMqdQ&sig=xECcFn3VPtBA34BVa9jiVHAsSiA&hl=en&sa=X&ved=0ahUKEwi7kZOe-L_RAhXpD8AKHcXRCyQQ6AEIIjAB#v=onepage&q=glenn%20fulcher%20point-biserial%20correlation&f=false
I think you’re too quick to dismiss the ceiling hypothesis. The fact that people aren’t getting 100% could mean that the test isn’t only measuring training – it’s also measuring general intelligence. The IQ part of the test doesn’t improve with training, so you plateau well short of 100%.
All tests measure intelligence along with whatever else. The plateau comes when you’ve saturated the “training” (or whatever else) part, at which point intelligence is all you’re testing. Note that the SAT subject tests, nominally tests of learning rather than aptitude, have equal predictive validity with the SAT when considered independently, and zero incremental predictive validity when considered jointly with the SAT. That tells you they’re testing exactly the same thing (but more wastefully, because you do have to study the material for a subject test, and you don’t for the SAT).
My ideas (most have aleady been shared by others here in the comments):
1. These exams might tap into forms of fluid intelligence (cramming everything the night before and multiple-choice questions), which we know start to gradually decline after the age of 20-22.
2. Teachers/principals do not like seeing average grades around 90-100%, so exams are changed until this is solved. This could be done by adding harder questions or less important/common topics, that are randomly missed by some students (this could be evaluated by having within-subjects comparisons instead).
3. Going beyond the data (and the main questions raised by your article), maybe 5 vs. 4 years of academia do not reflect an improvement in standardized pencil tests, but they could still have an effect on ones long term professional ability.
4. Also on the plus side:we are less likely to get impulsive young doctors, but of course that is a silly reason to force people to for pay more years of education.
Pure conjecture, but, I know that the SAT specifically is (or was) designed to have a scale of problem difficulty. (Making up all the following numbers). Maybe 50% of people could get 80% of the problems right with some reliability, but only 5% of test-takers could get 90% of the problems right, because that incremental 10% of the problems specifically belonged to a harder traunch. Then the last 10% of the problems are so tricky that only the top 0.1% of students could reliably get them right.
I would guess that most tests have this feature, to some degree, even if accidentally. The first year students get a 62% because 62% of the questions are pretty easy. Incremental gains over that inevitably reflect something about the “difficulty structure” of the test. Maybe each year a student is DOUBLING their knowledge, but each subsequent incremental 5% on the test is QUADRUPLING in difficulty, so the apparent score improvement is minuscule. (Again, pulling numbers out of the air here.)
Other people in the comments have already given undoubtedly more important causes for this phenomenon, but I do think this feature is always going to be present as well.
Sounds very likely.
Yeah, Scott’s argument assumes that all questions are equally hard.
The linear mapping of points total to skill is simply incorrect if the questions vary in difficulty.
The problem with this argument is that I have no alternative mapping to offer. This kills the discussion.
If I had to come up with one, I’d rank the individual questions by solution percentage, and… hope I got some good idea about how to think about this.
He does not assume this.
See this response.
I’m offering a different take on why the harder questions aren’t answered correctly, but I think moridinamael’s take is part of it, too.
I’m saying that considering 400 to 450 a bigger improvement than 450 to 480, assumes that the last 30 questions are as easy as the 50 before.
If the 30 are twice as hard, it’s actually a bigger improvement.
I think this is a different argument than the ceiling one.
I agree with you and I think it is something that Scott should have considered in his post.
I would guess it is a ceiling effect, and I don’t think saying “even the fifth years only get 76% correct” is looking at it the right way. While the theoretical ceiling is, in fact, 100% – a score that good might not be practically achievable for most people. When I think about standardized testing, I’ve always thought of it as each individual having their own individual unique ceiling, which for most (depending on the difficulty and scoring mechanism of the test) will be below a perfect score. Your own individual ceiling will depend on things like intellect, memory, etc. Natural ability that you can’t easily change. The ceiling is your maximum achievable score under perfect circumstances (studied heavily in an effective manner, got a lot of sleep the night before, have a good understanding of the test, etc.) As you progress in years, you gain more experiences, study more, etc. and come closer to hitting your own individual ceiling – and it may be that the average ceiling is in fact 76% rather than 100%. It could just be that the test is really hard and 100% is only achievable for uniquely brilliant people – most people will never get there no matter how much they study or how many experiences you throw at them or how often you remind them of things.
I don’t understand why this should be.
Suppose I have three facts, in order of difficulty/complicatedness:
1. Latuda is a brand name of a drug
2. Latuda is FDA-approved for bipolar disorder
3. Latuda is metabolized by the cytochrome 3A4 enzyme.
Every psychiatrist knows fact 1, most psychiatrists know fact 2, and probably few of them know fact 3. What does it mean to say somebody has a “personal ceiling” between facts 2 and 3? Why shouldn’t they be able to study about Latuda for longer and learn fact 3 too?
In theory they should, but in reality they don’t just have to know about Latuda, they have to know about, say, 100 different drugs. And certain people, due to some mixture of intellect and memory capacity, will be able to memorize and readily recall only 70, 80, or 90 such drugs (and the three relevant dimensions they have to know about said drugs). Studying can fill you “up to capacity” with facts but it cannot increase your capacity.
(That said, there probably are some methods by which you can improve your memory in general and thereby increase your capacity, but most people probably do not think to do these things as a part of “studying” for a test)
Your implicit hypothesis here is that forgetting is induced by learning — by learning fact #3, the doctor increases their risk of forgetting some other fact. There is a mountain of experimental psychological evidence about memory that fails to support this hypothesis.
Right, and I do concede this. I’m struggling to explain exactly what I’m talking about. It’s less “forgetting” and more “being less able to immediately recall without any sort of aid or assistance.” I don’t think those are quite the same thing but I’ll admit they are close.
I’m not saying that for every new fact you learn, you have to forget an old one. But I do think there’s something to be said for the idea that it’s easier to remember 10 things than it is to remember 100 things, and that “the most I can possibly remember about topic X (barring some sort of concentrated effort to improve memory generally)” is probably a real limit that exists and that varies from person to person.
Also I’d point out that my “ideal conditions” in terms of “maximum studying” does include SOME limits. Time spent actually working, sleeping, eating meals, etc. Even if a medical resident gave up ALL leisure time in lieu of studying, I don’t think it logically follows that they’d get 100% on the test.
Edit: I’d also add that there’s another difference between studying for a test and say, memorizing a list of U.S. Presidents. The resident does not know what questions are going to be on the test. So you have to memorize a lot of things, some of which will be useless, and there will likely be some things on the test you had no idea you were even supposed to know about.
I’d be curious about that evidence – the hypothesis strikes me as plausible but unfalsifiable (or at least hard to falsify), especially if the facts one forgets are unrelated to the facts one learns – the “absentminded professor” stereotype doesn’t refer to their forgetting things in their area of expertise, after all.
Where outright forgetting strikes me as less plausible is where the facts forgotten are related to the facts learned; there it might be more a matter of how long it takes for something to sink in, and whether there are maximum throughputs for facts as well as capacity.
>> Studying can fill you “up to capacity” with facts but it cannot increase your capacity.
> Your implicit hypothesis here is that forgetting is induced by learning
This is funny, because I would agree with Matt M’s statement while disagreeing that forgetting is induced by learning. I would say forgetting is induced by disuse. Studying something else is one of the infinitely many ways of not using a piece of information. But fundamentally, most of the forgetting at issue in this case happens immediately after the student hears the lesson; there is no period of disuse to force a forgetting because they don’t remember most of this stuff to begin with.
Going up the tree to Scott’s example, it’s pretty easy to get even a class of very dim students to remember “Latuda is metabolized by cytochrome 3A4” with high accuracy. It will be more work (for the teacher) to get the dimmer ones to remember this, and most, even at the brighter end, will tend to resist remembering. But this one sentence of eight words is within most everyone’s grasp.
However, the effort of remembering 500 sentences of basically the same form would take more than a lot of people are able to provide. It is beyond the limit of “I spend 100% of my waking hours reciting this nonsense” — most people can’t do it at all.
You could imagine a test that tested cognitive skills rather than memory of facts and a population of students of which a significant fraction were unable to perform certain cognitive skills on the test — I don’t know, proving theorems about elliptic curves or something. I’m at such a “personal ceiling” on Nethack for several years now because I keep doing impulsive things and dying; better executive function would presumably solve this problem. But you’re right that this is a better fit to a hypothesis of forgetting induced by the structure of the schooling system.
Incidentally, your fact #3 is a particularly dangerous thing for psychiatrists to forget, since it could result in a patient getting an overdose of an antipsychotic (even if one of the more innocuous antipsychotics) by way of drinking grapefruit juice or being put on ritonavir or clarithromycin — or, in the other direction, effectively going cold turkey on an antipsychotic if they get put on rifampicin. It seems like it would be pretty important for psychiatrists who prescribe Latuda to know to advise their patients not to drink grapefruit juice!
@Scott Alexander:
Who needs to know this piece of information? When do they actually use it in practice? Is it sufficient to be able to identify a situation when one should find out this piece of information?
In other words, it makes a “nice” standardized test question, but what effect does it have on clinical practice?
The vast bulk of people who end up working as psychiatrists won’t need to have memorized that fact, therefore we should not expect them to regurgitate this piece of information on their boards unless there is some incentive for them to spend as much time as possible trying to increase board scores, and less time learning how to actually practice psychiatry in a clinical setting.
I am very doubtful such incentives exist.
Someone who knows this fact abut Latuda, and is equally well informed about a number of other drugs, may correctly suspect that it’s worth researching whether there’s a problematic drug interaction which might not otherwise have been apparent.
If you are actually doing research on some metabolic problem, sure.
But if you are presented with a patient, and they aren’t a problematic case, you don’t need to know this fact. If they are and are not on Latuda, you don’t need to know this fact. If they are problematic, and on Latuda, you only need to know that the metabolizing of the drug is affected by some enzyme and if you suspect a problem metabolizing the drug, maybe you should look up what enzyme regulates this.
But you don’t need to have memorized this particular piece of information in order to make use of it later on.
Or if you’re prescribing more than one drug. There are an awful lot of drugs, and expecting all possible drug interactions to be helpfully described on the label is a tad optimistic. I was suggesting that knowing more about how the drugs work would give a doctor a better idea of when they really do need to dig into the literature and see if someone might have found a troublesome interaction.
Assuming the incentives don’t change much year to year, basically what you are saying is that the plateau represents the level of knowledge that people are incentivised to reach/maintain?
Is there any good research in general on incentives in education that could be used as a reference for this case?
It’s more that I am saying that getting better at standardized tests and getting better at clinical practice diverge at some point.
ETA:
As a practical example, I once was presented a standardized, computerized test of my ability to code in a certain language. It included a questions on which of two functionally equivalent addition operations executed faster.
Unless I am writing code at the bleeding edge of performance, knowing that question was irrelevant to my skill as a coder. If I need to optimize that close to the edge, I will start looking up those kinds of facts.
But in the everyday world it matters far, far, far more if my code is readable. And you can’t test that via a standardized multi-choice test.
Because the human brain is not a database and it has not evolved to just store collections of independent data.
It stores pieces of information depending to how they relate to other pieces of information and how useful it predicts they are.
If you are a clinical psychiatrist, then “Latuda is metabolized by the cytochrome 3A4 enzyme.” is a piece of information of no obvious use towards achieving your goals (e.g.
not getting sued for malpracticehealing the sick) and mostly unrelated to useful the information that you remember. Therefore you are likely to forget it.How much book learning vs patient care is done year over year? That is, do 1st year surgery residents spend most of their time hitting the books whereas 5th year residents spend most of their time wielding sharp instruments? I’d expect the test to essentially measure only book learning.
My layman’s understanding of how people learn would make me think that hands on practical work would be as good or better than reading a book, assuming the work covers the same or similar material to the book.
Yes, it’s that assumption I’m questioning. For instance, if in some operation there’s some structure a surgeon has to carefully avoid damaging, in practical work the name of the thing doesn’t matter, only knowing it’s there and not damaging it. But the test might require the name.
I guess there is a form of book learning (proper nouns and dates, the names of the doctor who invented the procedure and when, etc) that would not come up in the day to day work of being a surgeon but could be on the test.
Which would still be concerning, in that it would seem to indicate that some portion of the test is largely orthogonal to the job of being a surgeon, and so the test should probably be changed?
I haven’t seen this explanation posted so far; forgive me if I missed it. The reason people forget just as much as they learn in school, starting in the third year, is that the design of school is optimized for you to remember things for about two years.
(Also, this is my first time posting again now that the Reign of Terror is over. Hi again everybody!)
Research on spaced repetition (aka distributed practice) shows that the optimal spacing interval for presentations of a thing is about 10% or 20% of the time that you need to remember the thing. Consider the typical design of a school course: you practice some skill or memorization intensively for a few days, cram again before the midterm, cram again before the final, and then never again use it. A semester is maybe 16 weeks long, so we should expect you to retain that information for on the order of 160 to 320 weeks, which is three to six years; stuff you forgot to cram for the final will last only half as long.
If you’re at the end of four years of college, you might be saying, “This is crazy! I use things all the time that I learned in my first semester.” That’s selection bias: not only have you forgotten the things you learned three years ago that you don’t use all the time, you’ve forgotten about them entirely. If you go back and review problem sets you did in that first semester, you will probably be surprised at how much you covered.
This explanation does a reasonably good job of describing the observed phenomenon, which is that despite a great deal of variation among individuals, average performance improves substantially in the first year, moderately in the second year, very little in the third year, and not at all thereafter. By contrast, the proposed explanations for this plateauing phenomenon based on individual variation in intelligence do not predict such changes over time, as Scott points out.
The clear implication from spaced practice research is that our educational system is not just bad, but close to the worst that it could possibly be, with many fractal levels of practice massing:
❥ K-12 schooling is massed in 13 years, and higher education typically in 4–8 more, rather than being spread throughout a person’s entire life;
❥ taking courses on different topics each year guarantees the loss of most learning even before K-12 schooling ends;
❥ summer vacation guarantees the loss of nearly all new learning from the last months of the school year, and although this could be avoided by devoting those months exclusively to review of earlier material, this is not done;
❥ moving from unit to unit within each course, with little attention given to material from previous units, guarantees the loss of most learning from the course even before the end of the course;
❥ pre-scheduled large examinations incentivize students to “cram”, massing their practice in the days immediately before the examination, in order to cheat the examination into indicating a level of mastery of the material that they do not in fact possess, or, more precisely, will lose within a week or two;
❥ and, although the evidence for this is less clear in psychological studies, hour-long classes are very likely to result in poorer retention from one day to the next than if they were split into two half-hour chunks at different times of day. Instructors assign exercises to compensate somewhat for the loss of retention, but this worsens rather than improves the waste of time.
A more sensible system would be to devote, say, 90 minutes per day on average to learning-as-a-means-to-an-end, tapering down gradually from 180 minutes per day at 5 years old to 0 minutes at 75; but never ceasing to study anything once you’d started studying it, unless you’d changed your mind about whether it was worthwhile to know.
What would this optimized studying look like?
❥ On theoretical grounds, an exponentially-increasing spacing schedule for practicing each skill is likely best, although the experimental evidence for such “expanding spacing” is very thin at best.
❥ Probably flash cards, as used by current spaced-repetition systems like Mnemosyne and Anki, are close to the worst possible way to study (although highlighting textbooks and writing notes during lectures are worse still), except for things that really are best approached as rote memorization of meaningless lists; so an optimized learning system would focus more on exercises that combine existing skills with new ones just being developed.
❥ Individual tutoring has been robustly shown to increase educational achievement by two standard deviations over standard class instruction, the equivalent of 30 IQ points (or more, since IQ correlates imperfectly with educational achievement); tutoring another student or pair of students is probably a good way to increase your mastery of material you have already more or less learned, counting as part of your study time. This is convenient, since paying graduates of normal schools to tutor every student individually would be economically infeasible.
❥ Trying to perform a skill (e.g. by taking a test) before learning that skill has been robustly shown to improve educational achievement thereafter. Sometimes this is lumped with the spaced-practice effect, but it seems to happen even if you take the test immediately before you study the material. Intuitively, this makes sense: nobody forgets that ***** killed Dumbledore when they read the book, even though the information is only presented once, because they’ve already spent hours trying to figure out what will happen between those characters. It makes sense that you might have more motivation to learn a theory, as well as better judgment about what parts of the theory are important, if you’ve previously banged your head against the wall of a problem that you can solve with it.
All of the above is amply backed up by a century or so of psychological research; none of my factual claims are controversial. So why is our schooling system so far from being a decent educational system when judged by them?
This happens with K-12 test scores too. See Table 1 here: http://www.ncaase.com/docs/HillBloomBlackLipsey2007.pdf
The most compelling explanation for this that I’ve heard is kind of boring. Basically, we try to scale these tests so that differences are meaningful (e.g., advancing from 50 to 100 is the same as advancing from 100 to 150). However, as items become more complex, one can answer them incorrectly in more ways, meaning that increases in knowledge become decreasingly associated with increases in the probability of answering an item correctly. To illustrate, let’s say an easy question on a test is 5+8. Memorizing a single fact (5+8) will give me close to a 100% chance of getting the correct answer. In contrast, a difficult item might be (5+8)+(2+7)+(9+3). Here, if I learn the fact 5+8, I can still get the problem wrong if I don’t know 2+7, 9+3, 13+9, or 22+12! So, people who get that problem wrong will be much more heterogeneous in their knowledge of arithmetic than people who get 5+8 wrong.
Here is a more technical explanation of the problem:
http://onlinelibrary.wiley.com/doi/10.1111/jedm.12039/full
Is it possible that this is because of the forgetting curve you mentioned earlier? My experience with elementary education was that most things got reiterated year-to-year, and I just assumed that it was primarily to aid retention.
Not to say that schooling couldn’t be improved, and it’s entirely possible that kids spend too much time in school or are taught at the wrong ages. But I can see an argument for why the system might exist in the current repetition-focused state.
Could the effect be explained in part by ‘wrong learning’?
Something like, ‘I have an answer for 100% of the questions by third year, but 20-30% of my answers are wrong’
Any attempt to learn new information in the medical field has a 20-30% chance on average, of being learned, and remembered, incorrectly?
This might explain the apparent resistance to improvement?
Maybe different fields or different kinds of information/instructional methods have different averages for information learned incorrectly, and for medicine it just happens to be 20-30%.
Your theory of a sort of dynamic equilibrium holds up nicely if we actually look at the numbers.
Suppose we have a rate of knowledge gain (call it G), and lose a proportion (call it L) of our currently held knowledge in any given time. In other words, our rate of change for knowledge k is described by the differential equation dk/dt = G – Lk. We can solve this equation pretty easily to find that our knowledge at any given time k(t) is given by k(t) = Ce^(-Lx) + G/L, where G/L is the equilibrium where knowledge in = knowledge out (C is a constant of integration, in this case the difference between initial knowledge and equilibrium knowledge).
Here, we seem to be approaching an equilibrium of approximately 78% mean correct answers (in other words, G/L =~ 78 in our case). Plugging the data you gave in with that as an assumed equilibrium gives us an insanely good correlation: r = -.993. Playing with the exact equilibrium can get that even a little better (77.5% as an equilibrium gives r = -.995, r^2 = .99). This is a small sample, so it’s vulnerable enough to overfitting, but it seems intuitively plausible and that’s an awfully good fit even for a tiny data set.
—————————-
If we assume this sort of thing is going on all the time, it has interesting consequences. The relevant stat over the long term is what’s going on with G/L; in other words, we care about the ratio of leaning to forgetting. Changes in leaning, which would correspond to things like improved schooling, higher social class, more intellectual engagement, and so on, modify the numerator. Changes in forgetting, which would correspond to things like review and innate ability to retain information, modify the denominator.
I’d expect, as a rule, that G is more environmental and L is more heritable. But since L is already small and in a denominator, small changes in the absolute value of L can make huge differences to the ratio G/L – for example, going from retaining 90% of the things you know per year to 95% of the things you know per year *doubles* your equilibrium level of knowledge. Going from 90% to 99% multiplies it by 10.
As a teacher the implication seems to be that heavy review is likely to be much more effective at producing good long-term outcomes, provided that review is actually successful at reducing L. But if we have a short time-horizon and are purely interested in optimizing over that horizon, it’s mathematically possible that heavy emphasis on new information (i.e., on increased G at the cost of increased L) could result in better short-term outcomes at the cost of worse long-term results.
————
Does anyone have a data set that might be more comprehensive for testing this model? Say, a graph of scores on IQ tests by age?
I’m really not sure why this is mysterious. Isn’t this the general result for *any* learned skill?
I can’t help wondering if there’s some sort of ecological fallacy going on here. If we had access to unit record data, I’d expect to see some individuals plateauing out over a few years, some improving almost linearly, and some getting a high score in year 1 or 2 and then not improving at all.
Statistics like “There’s only a 17% chance that a randomly chosen first-year surgeon will know more about surgery than an average second-year. But there’s a 31% chance a second-year will know more than a third-year” are based on the assumption that both sets of data being compared are normally distributed with the same standard deviation. I’d actually expect second year students to show a lot less variation that first year.
Another theoretical possibility is that noone ever improves from one year to another, and the rising average is entirely due to dropouts. (I don’t actually believe this, just playing devil’s advocate!)
Is there any analysis out there that compares not just averages but distributions from year to hear? Anything using longitudinal unit level datasets?
I find it amusing that this grows in the retelling. You say 7th grade, the PT article says 6th grade, Benezet said 5th grade (in defense of the PT article Benezet talks about it in a weird way that I can only chalk up to the 30s, ‘Grade VI and ‘the fifth grade’ are used interchangeably, presumably because ‘Grade I’ is kindergarten).
More importantly, Benezet did include math on the lesson plan, he did not include *formal* math. No addition, subtraction, multiplication or division. But it did include measurement, counting, comparatives, and counting by increments. This might be an important difference. A contemporary article I dug up which talks about Benezet and others (most of whom got the same result, so there’s repetition even) says that kids come into school already having varying degrees of informal skill with numbers and what Benezet and others actually did was bring all the kids that would normally be slowing the class down up to speed.
You should know that this:
is not generally true and in fact the opposite effect often occurs: Retrieval Induced Forgetting
When something does or does not trigger this effect is a field of quite active research but the most popular hypotheses have to do with the amount of overlap in the representation of the information (which is an effect we can recreate in neural networks).
My prediction about the tests is that students generally study to the level they need to get internships in their desired specialties and spend the rest of their time either focused on more practical skills or just not working. IQ would be related to scores but the effect would be overstated without taking into account this study time difference. (People who want to go into neurosurgery will tend to have higher IQs and also study more because they have to get really high scores which makes the IQ effect seem larger than it really is).
I’m noticing in the threads that people’s desires for proper controls seems to go away when talking about IQ and I think people should be aware of this blind spot. Because IQ is in fact correlated with so much, saying any particular phenomenon is driven in large part by IQ is very difficult, which is a bit ironic I guess.
I think there’s an assumption you’re making at the beginning that may be throwing you off. You assume that these tests measure useful knowledge. I can speak for the USMLE and the radiology in-service exams: Some useful knowledge, but a lot of trivia. With this new assumption, you could say that the later year residents don’t stop caring, they just stop caring about studying for the test. I studied for 2 months for step 1, about a month for step 2, and 1-2 weeks for step 3. My percentile score was basically the same, but I think my raw score would have been lower each time. I assume that the rest of the country did the same, and we all did the same when the curves were calculated (our residency didn’t make a big deal about the in-service, so no one studied, and I can’t comment on that).
By the way, regarding transitional years: A lot of the residents are those who have already matched to specialty training programs (e.g., anesthesiology, dermatology, radiology, ophthalmology, radiation oncology) and are there because their programs require a year of general medicine. They can be run through surgery, internal medicine, or family medicine programs.
Diminishing returns are typical of realistic learning curves. These effects exist even in machine learning, with methods like artificial neural network.
Learning the easy stuff takes less time than learning the hard stuff, and depending on your intelligence/memory/effort/whatever, some stuff is hard enough that you will never learn it.
The problem with the study WRT: math is that it makes a fundamental assumption that “7th grade math” can’t be taught before 7th grade. If we’re simply not teaching small children anything of value, it is possible that is because little kids are such slow learners that they don’t pick up anything… but it is also possible that it is unrelated to developmental issues and is simply that most schools don’t push children at all during elementary school, and we could be teaching people algebra in third grade.
I know I’m not the average kid, but I learned about cell biology (at the sort of level they teach you in general biology in high school) in 2nd grade because I read a book about cell biology I checked out from the library. It wasn’t some ridiculous, over-my-head thing.
Heck, stuff I learned about evolution in books made my college evolution class a total joke.
It may be that early years of education aren’t very useful, but it may also be that they could be made much more useful and we simply haven’t.
You are so right. We’re not pushing kids to their full potential in the US. I grew up in Iran, where algebra was taught at 6th or 7th grade. We came to the US when I was in the 8th grade. I didn’t have to study for math here until about 10th or 11th grade, because we’d already learned it. We’re doing a great disservice to our kids here with our low expectations.
Are Iranian adults better at math than American adults?
I don’t think this is unique to medical school. I think this can be universally applied to almost any skill. When people first start learning something they very obviously don’t know anything about it. Most people will freely admit that they are novices, and are open to learning. After three years most people have a familiarity with the subject, and their mindset has changed. They have inculcated habits and opinions on the subject matter. They’re no longer a blank slate, for better or for worse. Some will believe that they’re better than they actually are.
Secondly, most (all?) of the low-hanging fruit for improvement will already have been plucked. Not everyone is willing to move on from the fun/easy areas of core competency to the boring/hard areas where they lack. There are certain skills that I have that I am simply unwilling to put in the grind necessary to greatly improve. I imagine this is as true for med students as it for anyone else.
Interestingly enough, The Economist uses a 3-year-rule with its “correspondents”: they all have to move every 3 years. For example, the current Berlin Bureau Chief and Germany correspondent, Andreas Kluth, had lived for 3 years in London, Hong Kong, and California (perhaps among other places) before moving back to his native Germany. If I recall correctly, either him or another correspondent said how this was just enough time to basically master a beat before moving on.
Vocabulary seems to plateau in middle age.
http://www.economist.com/blogs/johnson/2013/05/vocabulary-size
One question is whether athletes in different sports are getting better at earlier or later ages.
The use of steroids in baseball in the 1990s appeared to push peaks later than the traditional age 27.
Recently there have been some very young superstars, such as Mike Trout, who has been the best player in the American League from age 20 through 24.
It’s possible that star youngsters now get more and better tutoring at baseball than in the past when the attitude tended to be, “Let them play and see what happens.” Over the course of a typical baseball game, a youngster probably swings about, say, ten times. I suspect Mike Trout’s upbringing, in contrast, involved taking an order of magnitude more swings per day from an early age.
In the Netherlands, high potential boy soccer players don’t play that many games but they workout with a soccer ball one-on-one for several hours per day. American youths play a lot of soccer games, but their number of touches per game are only a few dozen. Not surprisingly, America doesn’t train many soccer prodigies. (On the other hand, American children may have more fun playing soccer than Dutch kids.)
In the Netherlands, the soccer association wants to have youth teams play 6 vs 6, instead of 11 vs 11, so the players get the ball more often (there are issues with having enough referees though).
11 on 11 is good exercise, but it mostly involves running around a lot without being terribly near the ball.
This phenomenon seems to pop up everywhere: we see it with exercise regimens, athletic performance, phase changes, and certain models of Evolution. Often times the rate of change hits several plateaus where progress is slight, and then improves again after a certain critical mass, before sometimes stabilizing at an asymptotic limit – it’s possible that the students only have enough time to hit their first plateau.
A few possible explanations:
1. There’s just something about the neurological structure of the brain that reduces the rate of improvement in a particular area.
2. As the tests are certainly g-loaded, eventually the test takers exhaust primary factors that they can improve on. .i.e. they’ve exhausted how well they can study for the test, memorize/understand the material, etc., and the remaining gap to the ceiling are things like higher level reasoning and working memory.
3. Their fading memory of earlier years cancels with new material they’ve learned – there’s a lot more to forget but a constant amount to take back in.
4. Understanding fundamentals adds far more marginal ability than more advanced concepts, .i.e. the low hanging fruit are taught in the early years.
5. There actually *is* senioritis, or rather fatigue, that doesn’t necessarily go away just because there are more or fewer years to go.