I.
I briefly snarked about Leslie et al (2015) last week, but I should probably snark at it more rigorously and at greater length.
This is the paper that concludes that “women are underrepresented in fields whose practitioners believe that raw, innate talent is the main requirement for success because women are stereotyped as not possessing that talent.” They find that some survey questions intended to capture whether people believe a field requires innate talent correlate with percent women in that field at a fairly impressive level of r = -0.60.
The media, science blogosphere, et cetera has taken this result and run with it. A very small sample includes: National Science Foundation: Belief In Raw Brilliance May Decrease Diversity. Science Mag: the “misguided” belief that certain scientific fields require brilliance helps explain the underrepresentation of women in those fields. Reuters: Fields That Cherish Genius Shun Women. LearnU: Study Findings Point To Source Of Gender Gap In STEM. Scientific American: Hidden Hurdle Looms For Women In Science. Chronicle Of Higher Education: Disciplines That Expect Brilliance Tend To Punish Women. News Works: Academic Gender Gaps Tied To Stereotypes About Genius. Mathbabe: “The genius myth” keeps women out of science. Vocativ: Women Avoid Fields Full Of Self-Appointed Geniuses. And so on in that vein.
Okay. Imagine a study with the following methodology. You survey a bunch of people to get their perceptions of who is a smoker (“97% of his close friends agree Bob smokes”). Then you correlate those numbers with who gets lung cancer. Your statistics program lights up like a Christmas tree with a bunch of super-strong correlations. You conclude “Perception of being a smoker causes lung cancer”, and make up a theory about how negative stereotypes of smokers cause stress which depresses the immune system. The media reports that as “Smoking Doesn’t Cause Cancer, Stereotypes Do”.
This is the basic principle behind Leslie et al (2015).
The obvious counterargument is that people’s perceptions may be accurate, so your perception measure might be a proxy for a real thing. In the smoking study, we expect that people’s perception of smoking only correlates with lung cancer because it correlates with actual smoking which itself correlates with lung cancer. You would expect to find that perceived smoking correlates with lung cancer less than actual smoking, because the perceived smoking correlation is just the actual smoking correlation plus some noise resulting from misperceptions.
So I expected the paper to investigate whether or not perceived required ability correlated more, the same as, or less than actual required ability. Instead, they simply write:
Are women and African-Americans less likely to have the natural brilliance that some fields believe is required for top-level success? Although some have argued that this is so, our assessment of the literature is that the case has not been made that either group is less likely to possess innate intellectual talent1.
So we will have to do this ourselves. The researchers helpfully include in their supplement a list of the fields they studied and GRE scores for each, as part of some sub-analysis to check for selectivity. GRE scores correlate closely with IQ and with a bunch of measures of success in graduate school, so this sounds like it would be a good test of the actual required ability hypothesis. Let’s use this to figure out whether actual innate ability explains the discrepancies better or worse than perceived innate ability does.
When I use these data I find no effect of GRE scores on female representation.
But these data are surprising – for example, Computer Science had by far the lowest GRE score (and hence projected IQ?) of any field, which matches neither other sources nor my intuition. I looked more closely and found their measure combines Verbal, Quantitative, and Writing GREs. These are to some degree anti-correlated with each other across disciplines2; ie those disciplines whose students have higher Quantitative tend to have lower Writing scores (not surprising; consider a Physics department versus an English department).
Since the study’s analysis included two measures of verbal intelligence and only one measure of mathematical intelligence, it makes more mathematical departments appear to have lower scores and lower innate ability. Certainly a measure set up such that computer scientists get the lowest intelligence of everyone in the academy isn’t going to find innate ability related to STEM!
Since the gender gap tends to favor men in more mathematical subjects, if we’re checking for a basis in innate ability we should probably disentangle these tests and focus on the GRE Quantitative. I took GRE Quantitative numbers by department from the 2014 edition of the ETS report. The results looked like this:
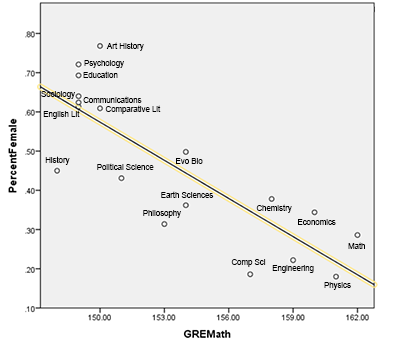
There is a correlation of r = -0.82 (p = 0.0003) between average GRE Quantitative score and percent women in a discipline. This is among the strongest correlations I have ever seen in social science data. It is much larger than Leslie et al’s correlation with perceived innate ability3.
Despite its surprising size this is not a fluke. It’s very similar to what other people have found when attempting the same project. There’s a paper from 2002, Templer and Tomeo, that tries the same thing and finds r = 0.76, p < 0.001. Randal Olson tried a very similar project on his blog a while back and got r = 0.86. My finding is right in the middle.
A friendly statistician went beyond my pay grade and did a sequential ANOVA on these results4 and Leslie et al’s perceived-innate-ability results. They found that they could reject the hypothesis that the effect of actual innate ability was entirely mediated by perceived innate ability (p = 0.002), but could not reject the hypothesis that the effect of perceived-innate-ability was entirely mediated by actual-innate ability (p = 0.36).
In other words, we find no evidence for a continuing effect of people’s perceptions of innate ability after we adjust for what those perceptions say about actual innate ability, in much the same way we would expect to see no evidence for a continuing effect of people’s perceptions of smoking on lung cancer after we adjust for what those perceptions say about actual smoking.
II.
Correlation is not causation, but a potential causal mechanism can be sketched out.
I’m going to use terms like “ability” and “innate ability” and “genius” and “brilliance” because those are the terms Leslie et al use, but I should clarify. I’m using them the way Leslie et al seem to, as a contrast to hard work, the internal factors that give different people different payoffs per unit effort. So a genius is someone who can solve difficult problems with little effort; a dullard is one who can solve them only with great effort or not at all.
This use of “innate ability” is not the same thing as “genetically determined ability”. Genetically determined ability will be part of it, but there will also be many other factors. Environmental determinants of intelligence, like good nutrition and low lead levels. Exposure to intellectual stimulation during crucial developmental windows. The effect of steretoypes, insofar as those stereotypes globally decrease performance. Even previous training in a field might represent “innate ability” under this definition, although later we’ll try to close that loophole.
Academic programs presumably want people with high ability. The GRE bills itself as an ability test, and under our expanded definition of ability this is a reasonable claim. So let’s talk about what would happen if programs selected based solely on ability as measured by GREs.
This is, of course, not the whole story. Programs also use a lot of other things like grades, interviews, and publications. But these are all correlated with GRE scores, and anyway it’s nice to have a single number to work with. So for now let’s suppose colleges accept applicants based entirely on GRE scores and see what happens. The STEM subjects we’re looking at here are presumably most interested in GRE Quantitative, so once again we’ll focus on that.
Mathematics unsurprisingly has the highest required GRE Quantitative score. Suppose that the GRE score of the average Mathematics student – 162.0 – represents the average level that Mathematics departments are aiming for – ie you must be this smart to enter.
The average man gets 154.3 ± 8.6 on GRE Quantitative. The average woman gets 149.4 ± 8.1. So the threshold for Mathematics admission is 7.7 points ahead of the average male test-taker, or 0.9 male standard deviation units. This same threshold is 12.6 points ahead of the average female test-taker, or 1.55 female standard deviation units.
GRE scores are designed to follow a normal distribution, so we can plug all of this into our handy-dandy normal distribution calculator and find that 19% of men and 6% of women taking the GRE meet the score threshold to get into graduate level Mathematics. 191,394 men and 244,712 women took the GRE last year, so there will be about 36,400 men and 14,700 women who pass the score bar and qualify for graduate level mathematics. That means the pool of people who can do graduate Mathematics is 29% female. And when we look at the actual gender balance in graduate Mathematics, it’s also 29% female.
Vast rivers of ink have been spilled upon the question of why so few women are in graduate Mathematics programs. Are interviewers misogynist? Are graduate students denied work-life balance? Do stereotypes cause professors to “punish” women who don’t live up to their sexist expectations? Is there a culture of sexual harassment among mathematicians?
But if you assume that Mathematics departments are selecting applicants based on the thing they double-dog swear they are selecting applicants based on, there is literally nothing left to be explained5.
I am sort of cheating here. The exact perfect prediction in Mathematics is a coincidence. And I can’t extend this methodology rigorously to any other subject because I would need a much more complicated model where people of a given score level are taken out of the pool as they choose the highest-score-requiring discipline, leaving fewer high-score people available for the low-score-requiring ones. Without this more complicated task, at best I can set a maximum expected gender imbalance, then eyeball whether the observed deviation from that maximum is more or less than expected. Doing such eyeballing, there are slightly fewer women in graduate Physics and Computer Science than expected and slightly more women in graduate Economics than expected.
But on the whole, the prediction is very good. That it is not perfect means there is still some room to talk about differences in stereotypes and work-life balance and so on creating moderate deviations from the predicted ratio in a few areas like computer science. But this is arguing over the scraps of variance left over, after differences in mathematical ability have devoured their share.
III.
There are a couple of potentially very strong objections to this hypothesis. Let me see if I can answer them.
First, maybe this is a binary STEM vs. non-STEM thing. That is, STEM fields require more mathematical aptitude (obviously) and they sound like the sort to have more stereotypes about women. So is it possible that my supposedly large sample size is actually just showing an artifact of division into these two categories?
No. I divided the fields into STEM and non-STEM and ran an analysis within each subgroup. Within the non-STEM subgroup, there was a correlation between GRE Quantitative and percent female in a major of -0.64, p = 0.02. It is completely irresponsible to do this within the STEM subgroup, because it has n = 7 which is too small a sample size to get real results. But if we are bad people and do it anyway, we find a very similar correlation of -0.63. p is only 0.12, but with n=7 what did you expect?
Both of these correlations are higher than Leslie et al were able to get from their entire sample.
Second, suppose that it’s something else driving gender-based patterns in academia. Maybe stereotypes or long hours or whatever. Presumably, these could operate perfectly well in undergrad. So stereotypes cause lots of men to go into undergraduate math and lots of women to go into undergraduate humanities. The men in math classes successfully learn math and the women in humanities classes successfully learn humanities. Then at the end of their time in college they all take the GRE, and unsurprisingly the men who have been taking all the math classes do better in math. In this case, the high predictive power of mathematical ability would be a result of stereotypes, not an alternative to them.
In order to investigate this possibility we could look at SAT Math instead of GRE Quantitative scores, since these would show pre-college ability. SAT scores show a gap much like that in GRE scores; in both, the percentile of the average woman is in the low 40s.
Here is a graph of SAT Math scores against percent women in undergraduate majors:
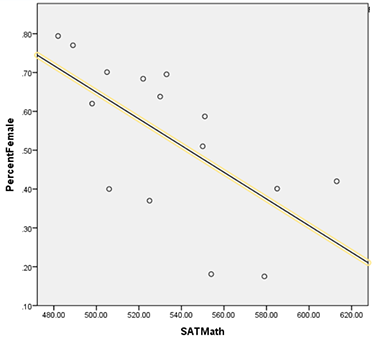
SAT Math had a correlation of -0.65, p = 0.016.
This correlation is still very strong. It is still stronger than Leslie et al’s correlation with perceived required ability. But it is slightly weaker than the extremely strong correlation we find with GRE scores. Why?
I can’t answer that for sure, but here is a theory. The “undergraduate major” data is grabbed from what SAT test-takers put down as their preferred undergraduate major when they take the test in (usually) 11th grade. The “percent female” data is grabbed from records of degrees awarded in each field. So these are not exactly the same people on each side. One side shows the people who thought they wanted to do Physics in 11th grade. The other side shows the people who ended up completing a Physics degree.
The people who intend to pursue Physics but don’t end up getting a degree will be those who dropped out for some reason. While there are many reasons to drop out, one no doubt very common one is that the course was too hard. Therefore, the people who drop out will be disproportionately those with lower mathematical ability. Therefore, the average SAT Math score of 11th grade intended Physics majors will be lower than the average SAT Math score of Physics degree earners. So the analysis above likely underestimates the average SAT Math score of people in mathematical fields. This could certainly explain the lower correlation, and I predict that if we could replace our unrepresentative measure of SAT scores with a more representative one, much of the gap between this correlation and the previous one would close.
These data do not rule out simply pushing everything back a level and saying that these stereotypes affect what classes girls take in middle school and high school. Remember, we using “ability” as a designation for a type of excellence, not an explanatory theory of it. This simply confirms that by eleventh grade, the gap has already formed.7.
Third, perhaps SAT and GRE math tests are not reflective of women’s true mathematical ability. This is the argument from stereotype threat, frequently brought up as reasons why tests should not be used to judge aptitude.
But this is based on a fundamental misunderstanding of stereotype threat found in the popular media, which actual researchers in the field keep trying to correct (to no avail). See for example Sackett, Hardison, and Cullen (2004), who point out that no research has ever claimed stereotype threat accounts for gender gaps on mathematics tests. What the research found was that, by adding an extra stereotype threat condition, you could widen those gaps further. The existing gaps on tests like the SAT and GRE correspond to the “no stereotype threat” control condition in stereotype threat experiments, and “absent stereotype threat, the two groups differ to the degree that would be expected based on differences in prior SAT scores”. Aronson and Steele, who did the original stereotype threat research and invented the field, have confirmed that this is accurate and endorsed the warning.
Anyway, even if the pop sci version of stereotype threat were entirely true and explained everything, it still wouldn’t rescue claims of bias or sexism in the sciences. It would merely mean that the sciences’ reasonable and completely non-sexism-motivated policy of trusting test scores was ill-advised.8
Fourth, might there be reverse causation? That is, suppose that there are stereotypes and sexism restricting women’s entry into STEM fields, and unrelatedly men have higher test scores. Then the fields with the stereotypes would end up with the people with higher test scores, and it would look like they require more ability. Might that be all that’s happening here?
No. I used gender differences in the GRE scores to predict what scores we would expect each major to have if score differences came solely from differences in gender balance. This predicted less than a fifth of the variation. For example, the GRE Quantitative score difference between the average test-taker and the average Physics graduate student was 9 points, but if this were solely because of differential gender balance plus the male test advantage we would predict a difference of only 1.5 points. The effect on SAT scores is similarly underwhelming.
But I think the most important thing I want to say about objections to Part II is that, whether they’re correct or not, Part I still stands. Even if the correlation between innate ability and gender balance turns out to be an artifact, Leslie et al’s correlation between perceived innate ability and gender balance is still an artifact of an artifact.
IV.
A reader of an early draft of this post pointed out the imposingly-named Nonlinear Psychometric Thresholds In Physics And Mathematics. This paper uses SAT Math scores and GPA to create a model in which innate ability and hard work combine to predict the probability that a student will be successful in a certain discipline. It finds that in disciplines “such as Sociology, History, English, and Biology” these are fungible – greater work ethic can compensate for lesser innate ability and vice versa. But in disciplines such as Physics and Mathematics, this doesn’t happen. People below a certain threshold mathematical ability will be very unlikely to succeed in undergraduate Physics and Mathematics coursework no matter how hard-working they are.
And that brought into relief part of why this study bothers me. It ignores the pre-existing literature on the importance of innate ability versus hard work. It ignores the rigorous mathematical techniques developed to separate innate ability from hard work. Not only that, but it ignores pre-existing literature on predicting gender balance in different fields, and the pre-existing literature on GRE results and what they mean and how to use them, and all the techniques developed by people in those areas.
Having committed itself to flying blind, it takes the thing we already know how use to predict gender balance, shoves it aside in favor of a weird proxy for that thing, and finds a result mediated by that thing being a proxy for the thing they are inexplicably ignoring. Even though it just used a proxy for aptitude to predict gender balance, everyone congratulates it for having proven that aptitude does not affect gender balance.
Science journalism declares that the myth that ability matters has been vanquished forever. The media take the opportunity to remind us that scientists are sexist self-appointed geniuses who use stereotypes to punish women. And our view of an important issue becomes just a little muddier.
I encourage everyone to reanalyze this data and see if I’m missing something. You can find the GRE data I used here and the SAT data here (both in .xlsx format).
Footnotes
1. They cite for this claim, among other things, Stephen Jay Gould’s The Mismeasure Of Man
2. Beware the ecological fallacy; these scores are still positively correlated in individuals.
3. It was also probably more highly significant, but I can’t tell for sure because (ironically) their significance result wasn’t to enough significant digits.
4. There was a small error in the percent of women in Communications in the dataset I provided them with, so these numbers are off by a tiny fraction from what you will get if you try to replicate. I didn’t feel comfortable asking them to redo the entire thing, but the small error would not have changed the results significantly, and the tiny amount it would have changed them would have been in the direction of making the innate ability results more striking rather than less.
5. Although Leslie et al focused on women, they believe their results could also extend to why African-Americans are underrepresented compared to European-Americans and Asian-Americans in certain subjects. They theorize that European and Asian Americans, like men, are stereotyped as innately brilliant, but African-Americans, like women, lack this stereotype. I find this a bit off – after all, in the gender results, they contrasted the male “more innately brilliant” stereotype with the female “harder-working” stereotype, but African Americans suffer from a stereotype of not being hard-working, and Asian-Americans do have a stereotype of being hard-working, even more so than women. Anyway, this is only a mystery if you stick to Leslie et al’s theory of stereotypes about perceived innate ability. Once you look at GRE Quantitative scores, you find that whites average 150.8, Asians average 153.9, and blacks average 143.7, and there’s not much left to explain.
6. It’s hard to correlate SAT scores with majors, because the SAT data is full of tiny vocational majors that throw off the results. For example, there are two hundred people in the country studying some form of manufacturing called “precision production”, they’re almost all male, and they have very low SAT scores. On the other hand, there are a few thousand people studying something called “family science”, they’re almost all women, and they also all have very low SAT scores. The shape of gender*major*SAT scores depends almost entirely on how many of these you count. I circumvented the entire problem by just counting the fields that approximately corresponded to the ones Leslie et al counted in their graduate-level study. I tried a few different analyses using different ways of deciding which fields to count, and as long as they were vaguely motivated by a desire to include academic subjects and not the vocational subjects with very low scores, they all came out about the same.
7. The argument that stereotypes cause boys to take more middle school and high school math classes than girls is somewhat argued against by the finding that actually girls take more middle school and high school math classes than boys. However, there are some contrary results; for example, boys are more likely than girls to take the AP Calculus test. This entire area gets so tangled up in differing levels of interest and ability and work-ethic that it’s not worth it, at my level of interest and ability and work ethic, to try to work it out. The best I can say is that the gap appears by the time kids take the SAT in 11th grade.
8. I can’t help adding that I continue to believe that the stereotype threat literature looks like a null field which continues to exist only through publication bias and experimenter effects. The funnel plot shows a clear peak at “zero effect” and an asymmetry indicating a publication bias for positive results (for some discussion of why I like funnel plots, see here.) And a closer look at the individual research shows this really disturbing pattern of experiments by true believers finding positive effects, experiments by neutral parties and skeptics not finding them, replication attempts failing, and large real-world quasi-experiments turning up nothing – in a way very reminiscent of parapsychology. Although I am far from 100% sure, I would tentatively place my money on the entire idea of stereotype threat vanishing into the swamp of social psychology’s crisis of replication.
















Why do high school girls consistently outperform boys in math, and then this reverses in college?
edit: I should check things before I post. apparently they don’t. https://destinyhub.net/images/destinyhub/smilies/mysterysolved.gif
I’m not sure what makes you think they don’t. There are a few things going on here.
1. Girls get better math grades than boys in high school. In fact, girls get better grades than boys in everything in high school. You know how the Leslie et al paper talks about the stereotypes that girls are harder-working but men are smarter? This seems to be based off of the AFAIK correct observation that high school girls get better grades but high school boys better standardized test scores (at least in math).
2. The average girl outperforms the average boy at math, but there are more men at both higher and lower levels of the ability distribution. As you advance to higher education, you’re lopping off more of the bottom of the distribution (ie mostly just smart people go to college), which cuts out the large number of underperforming men, raising men’s relative position.
3. The nurture side of the nature-vs.-nurture dichotomy suggest that men and women are more interested in conforming to sex stereotypes after puberty, given the whole “dating” thing.
4. And the nature side of same suggest that sex-specific mental differences only appear after puberty, once the adult balance of sex hormones has been established.
yea..the SD of IQ of the bell curve for women is smaller. Fewer outliers. Probably could explain why gifted and special ed classes mostly have boys. That’s what Larry Summers alluded to, but perhaps some figments of truth were overlooked in the controversy that ensured?
Warning: I don’t think stuff like “the left shouted him down because the truth hurts” is helping this discussion, and I’ll probably ban you if you keep up in that vein.
reworded it
I don’t know how else anyone could possibly describe Nancy Hopkins’ motives in leaking an off-the-record talk to town’s paper of record. The whole conference was supposed to be off-the-record so that people could have a grown-up conversation about the true explanations for why the gender gap might exist. Once Larry Summers engaged in the thoughtcrime of considering hypotheses other than Larry Summers is a sexist pig, he was publicly pilloried as a sexist pig. This is the sort of kafkatrap pioneered by marxists for subverting discourse (especially academic discourse) to advance their totalitarian objectives.
Could you offer documentation of the claim that the conference was off-the-record?
Why, yes I can!
But you could also have read the Globe article that notes that the conference was a private, invitation-only event.
Of course, the very idea of any event being ownlifewise is thoughtcrime. The Globe wants you to know that Larry Summers is a doubleplusungood duckspeaker.
“I don’t know how else anyone could possibly describe Nancy Hopkins’ motives in leaking an off-the-record talk to town’s paper of record.”
Even if the description is accurate, I think the use of the term “the Left” threatens to take this in an unnecessary and worrying direction and turn off some people who might be marginally willing to hear these things out.
I think it is very helpful. In what way was that not what happened? And what is also happening regarding “minorities” (i.e. non-Asian, non-Whites)?
It’s unhelpful because it makes it tribal. I see a comment like that, my natural inclination isn’t “Man Nancy Hopkins is terrible”, it’s “Oh yeah? Well $CONSERVATIVE is a jerk too because $THING!”.
Neither of those really add much to a discussion of explanations of gender gap in STEM fields, and they make everyone upset.
The trouble with this mini-debate is there’s simply no way to fight the nothingness if we don’t have a name for it. I saw a documentary on this issue when I was a kid.
Hypothesis #1: The nothingness is not real, it’s a boogeyman made up by bad people.
Hypothesis #2: The nothingness is a bad name that won’t help us fight it.
I think it’s beyond question that the blogger and STC readers/commenters think there is something real being referred to in GE’s comment. I am partial to the argument that he makes a shitty Atreyu. Nothing personal GE, but I just don’t think “the left” is going to stop the world from rotting out.
How else should it be described? Genuinely curious. That’s exactly how I perceive it.
Edit: you say you don’t like “The Left”. Since when? You use similar group labels all the time.
While I can see the point to avoiding needless tribalism, pretending that tribes do not exist or refusing to name and criticize them hardly seems to be an ideal solution.
I find the the big problem with saying “The Left” (or a different group in a different situation) did this thing or that thing is that it avoids the fact that actual people did those things. As good as human brains are at assigning people into groups, no person is actually 100% “The Left”. It was not a massive group of people who leaked Summers’ remarks, it was one person, and it wasn’t everyone on the Left, or even probably the majority of people on the Left, who talked about it*. This won’t stop people from being tribal, but calling people out by name will help keep you from thinking quite so tribally (or at least it seems to help me).
I also find that when I call people out by name instead of group I get much much less frustrated with the world. The world is just seems so much more rational (to me) when they’re individuals.
*I’m not an expert on this by any means, nor have I done even the most basic google research on it to write this post. I’m just referring to the current topic of discussion.
So first for clarification – RCF said below that ‘the Left’ doesn’t mean ‘every person who is left of centre’. I’ve been taking those two terms as equivalent.
I guess the heuristic I’d be endorsing here is “Try not to make it about tribes unless it absolutely must be, and when you do make it about tribes try to be specific about what the relevant subset is”. It’s the difference between saying “The Left sucks because of $PERSON” and “The BDS movement sucks because of $PERSON”, where it’s the same person in both. The former reads, at least to me, like the classic tactic of attacking an entire group via the most ridiculous people involved with that group (Not that I’m saying the BDS movement is ridiculous, it’s just an example). The latter can’t do that as easily because it’s got a much smaller group to hit, and because the subgroup you’re arguing against is more uniform in belief.
Maybe “the left” means “left of center” but “the Left” means Marxists. (This has nothing to do with group responsibility.)
@pneumatik
“It was not a massive group of people who leaked Summers’ remarks, it was one person, and it wasn’t everyone on the Left, or even probably the majority of people on the Left, who talked about it*.”
But it’s not about specific people. That’s the point. Leftist Social Justice Warriors, or whatever you want to call them, are not just a bunch of isolated people doing isolated things. They may not be explicitly coordinating their action, but they are engaged in a campaign of common purpose, and there is emergent phenomenon arising from their behavior. The point is to create a social norm in which saying “One hypothesis that people are considering is that men have a higher IQ variance”, even if you don’t actually say that’s your preferred explanation, is not acceptable behavior. The point is to create the impression of social consensus. So, no, it’s not just a matter of a bunch of individuals. There was a widespread media effort to paint Sumners as sexist. For instance, there was quote from someone in I think Parade saying that Sumners thinks that girls can’t do math. Should I have recorded who was quoted, so that in all further conversations, I can refer to her specifically, rather than referring to The Left? She was just some random person that Parade found to spout SJW bullshit. She was just one link in a game of telephone of one person misrepresenting Sumners’ words, and then someone else promulgating their own misrepresentation based on that. It was Parade that chose to print this, and to treat it as a legitimate point of view. So what specific person do I blame for that? Whatever anonymous Parade employee who got the quote? Their editor? The editor in chief? This is institutionalized bullshit. Trying to figure out who specifically is responsible for the “Sumner is sexist” meme is like trying to decide who’s responsible for the “black people are criminals” meme.
If this were a matter purely of “innate ability and what fields require which”, there would be nothing controversial about “men do better in fields that require maths than women because more men have innate mathematical ability than women do”.
But of course, it’s nothing that simple. Underneath it all is the whole “Sorry, ladies, women are stupider than men and we can prove it with science. Look! You need to be Really Smart to do maths. And a lot more guys than gals end up doing maths and in maths-related fields. Therefore, men in general are Really Smart and women are not.”
What makes it even more toxic is when you bring race in, which is why I’m not even going to touch that side of it with a bargepole.
But yes – I think the trouble with the study, and the reaction to it, and the fuss about “it’s all down to stereotypes” is the quantifying of one type of intelligence or one field of ability as better or superior or qualitatively and objectively more excellent than any other.
Maths is the best science. Mathematical intelligence is the best intelligence. Men are smarter than women because men are better at maths. Maths is so good because it gives us all these cool things like science and technology.
You don’t want to live in a world without antibiotics and computers, do you? You could happily live in a world without poetry and art history, on the other hand!
So let the ladies go into the fields their inferior brains can handle and let the men handle the Real Important Big Work.
That’s the kind of argument we’re going to get embroiled in, I’m very much afraid!
I’m having trouble following your point here, Deiseach. Is it “the claim that men have larger standard deviation in mathematical ability / intelligence is readily turned into a simplistic men > women claim, therefore Larry Summers shouldn’t (ethically) have said the thing he said”? Because that kind of rules out any statement that can be reduced to simplistic, wrong, harmful – for example, religion, because divine command ethics (EDIT: originally said ‘theology’ here, which wasn’t what I meant).
Or is it just the point that Larry Summers was walking into a minefield because it’s very easy for other people to make the simplistic claim / read the simplistic claim in what he’s saying, so it’s unfortunate that he got blown up, but kind of expected?
>If this were a matter purely of “innate ability and what fields require which”, there would be nothing controversial about “men do better in fields that require maths than women because more men have innate mathematical ability than women do”.
In what universe?
> You don’t want to live in a world without antibiotics and computers, do you? You could happily live in a world without poetry and art history, on the other hand!
FWIW, I am a man, and from my own personal point of view this statement is literally true. YMMV.
That’s not the kind of argument that was going to happen. That was the kind of argument you tried to turn it into.
James, I know very little about the Larry Summers controversy (other than What I Saw In The News Media, which is probably about as helpful for understanding it as reading the tealeaves).
But the broader problem here is that it’s not a simple matter of “unbiased, objective truth: here are the graphs, here are the statistics, here are the conclusions that can reliably be drawn from them”.
Those objective conclusions will be seized on by everyone with an axe to grind, which is pretty much everyone. One side will be adamant that this is proof of institutional, cultural and social bias; the other side will be waving the results around that this proves women/non-White, non-Asian minority are naturally less able than men/White, Asian people. It’s not racism or sexism, it’s plain science.
We’re also making a lot of assumptions here, and making conclusions based on those assumptions:
(1) Mathematics demands high intelligence and even genius [Me: okay, I’ll accept that. Seems to be factually true. No argument there.]
(2) Mathematical ability is the highest form of intelligence; forget being really good at anything outside the hard sciences (and those are getting rigorously delimited; biology is not a hard science! The Ernest Rutherford quote in its variant forms about “Physics is the only real science, the rest are just stamp collecting”) [Me: Now we’re beginning to wade into the deep waters. We’re moving from ‘here are the test scores’ to ‘making assumptions about the test scores’ that the test scores, in themselves, don’t tell us much one way or the other]
(3) Men have more mathematical ability and at a higher level than women/Whites and Asians have more mathematical ability and at a higher level than non-White, non-Asians [Me: If we festoon this statement with qualifications and stick to the data, then I’ll accept it, but I see trouble ahead]
(4) Men/Whites and Asians – more mathematical ability than women/non-Whites, non-Asians = Men/Whites and Asians – more intelligent than women/non-White non-Asians [and following on from that]
(5) Women/non-Whites, non-Asians are naturally less intelligent, naturally inferior. Nobody is blaming anybody for being at fault, this is all down to biology, you can’t argue with the science (see the test scores!) Training, education and hard work won’t make up for lack of inherent ability. You can’t make a silk purse out of a sow’s ear. Some peoples are natural inferiors/natural slaves. This is not sexism or racism, this is scientific fact.
(6) Affirmative action means replacing able men/able Whites and Asians with less able women/less able non-Whites, non-Asians. This isn’t me saying this, this is being argued in the comments on this very post. The idea that you go out and find the most able women or minorities doesn’t seem to be in play; it’s either ‘smart able men’ or ‘less smart less able women’.
There seems to be a conflation between ‘fewer women will be at the genius end level than men’ and ‘therefore getting in more women means getting in less able candidates’. I don’t agree; I think it simply means spreading your nets wider. If you only have ten women out of two hundred who are on the same level as thirty men out of two hundred, then interview one thousand or two thousand women and take the smartest ones out of that who score as well as the men do! You don’t have to take “well, we need thirty more women, we just have to take the first thirty who turn up, we can’t choose the smarter ones”.
EDIT: But what if we can’t get two thousand women who want to study maths or physics? Okay, then we don’t get a 50/50 gender balance class. I’d be perfectly happy with that: out of the pool of candidates who applied, we picked the top thirty (or forty or nine thousand or whatever the hell number you like) for the thirty or forty or nine thousand class places on offer, and that means we have twenty men and ten women who scored high enough to get in.
But you know as well as I do it wouldn’t rest there. There would be screeching and fighting over why more women didn’t apply: stereotypical bias means women are discouraged versus women just aren’t smart enough!
And that’s a fight I hate, don’t want to get involved in, but as a female human being have very little choice about; e.g. I’m hopeless at maths. This is because I’m dyscalculic, not because I’m female. I’m much better at verbal and written skills. But there will be someone out there willing to argue that ONLY mathematical ability is TRUE intelligence, and even men gifted with verbal or artistic ability are not REALLY intelligent, so women – who in the main are not as smart even as the non-mathematical men (see the list of Great Artists, Great Authors, Great Composers etc. to back up this argument) – really are NOT intelligent, so women, know your limits!
Deiseach, I really feel ya. Not going to get involved here, but I really agree, despite not being 1) a female-socialized woman, or 2) even slightly interested in math.
@Deiseach 9:29:
Regarding your 2), it seems to me that the people most strongly promoting the idea that “math success is best success” are those who are pushing strongly to label the current male-female ratio in STEM a Discrimination Crisis That Must Be Solved, while ignoring the highly female-skewed ratio in other fields, and in higher ed overall.
For 5), who on here is saying that women are “naturally inferior” at anything other than average math scores (a hypothesis that the data supports)? And who is saying that that makes them “inferior” human beings? That’s a scare tactic to try to get us to shut up about this, which is bad for understanding the issue.
The consensus here seems to be that the highest performing math students are disproportionately male, and there is probably an “innate” component. Women are probably superior in other forms of intelligence, but that’s not as relevant here since we’re talking exclusively about STEM (and see above for why that’s not really our fault).
Honestly, the only people I’ve really seen making any “women are strictly inferior” statements are you and others trying to build a slippery slope argument that this whole thing is just Too Dangerous to Talk About, so we should pretend we never heard it.
Regarding 6), replacing more able (on traditional metrics) candidates of one group with less able candidates of a favored group is exactly how real world affirmative action works. At the admissions level every time it’s been looked at quantitatively, the admits in the favored group in an affirmative action scheme have significantly lower average scores on traditional metrics than the disfavored group.
Talk of “casting a wider net” is nice, but in practice no one on the affirmative action side is doing that, or at least not doing it exclusively.
Honestly I’d have for more tolerance for affirmative action supporters if they’d stop the motte-and-bailey game and admit that affirmative action discriminates on the margins, and indeed has to because that’s the primary operating principle. Every affirmative action supporter I know is aware of this, and supports it because they think it’s justified, but will inevitably try to steer away from it with talk of “holistic admission standards” or some such confounding language. Own it!
I believe some places (Caltech for example) do still stick to extra recruiting efforts for women, ie casting a wider net, not lowering standards. The phrase “affirmative action” just isn’t used to refer to this practice.
Deiseach:
So you’re saying we should keep things as they are, because otherwise there is a chance that bad people will take advantage of it and everything will go wrong?
“There seems to be a conflation between ‘fewer women will be at the genius end level than men’ and ‘therefore getting in more women means getting in less able candidates’. I don’t agree; I think it simply means spreading your nets wider. If you only have ten women out of two hundred who are on the same level as thirty men out of two hundred, then interview one thousand or two thousand women and take the smartest ones out of that who score as well as the men do! You don’t have to take “well, we need thirty more women, we just have to take the first thirty who turn up, we can’t choose the smarter ones”.”
Perhaps this logical fallacy needs a name (or does it?). An assertion is made that we’re at an optimization frontier, and therefore it’s impossible to increase one metric without decreasing another, and someone comes back saying that we can increase one of the metrics by simply moving to a different frontier. Blrrg.
Look, we have a particular recruitment budget. Given that budget, we’ll find a particular pool of candidates. Given that pool of candidates, it’s impossible to increase the percentage of women without decreasing the quality. Saying “Well, we can increase the number of women by casting a wider net” is simply not a valid argument. You’re comparing “cast a wider net for women” to “don’t cast a wider net”, which is not the correct comparison. The correct comparison is “spend a bunch of resources casting a wider net for women” versus “cast a wider net in general, in which case most of the additional people you get will be men, and then you’re back to where you started”. If you have a bunch of extra money lying around that you can use casting a wider net for women, then you could use this money finding additional men. By choosing to use it on women, you’re getting a lower quality than what you would get if you you used it on the general population. You can’t just put some resources aside and pretend that they’re only available for your pet agenda.
Optimizing for one terminal value means sacrificing others. Period.
Having to actually explain this, on a rationalist site … arghhh.
I think you are being elitist here. The gender difference is mainly in standard deviation, not average, which results in more top-performing, high-powered men, but also more stupid men in prison or in the homeless ward.
Why only the top, only the elite seems to matter in these Internet discussions?
Especially when terms like “The Left” are brought into play: isn’t “The Left” supposed to care about largely the least well off people? Care more about the homeless wards than the corporate boards?
Related question: where is that kind feminist discussion about work and caree that is not about empowering career dreams but toiling away to pay bills: so about 80-90% of jobs?
Isn’t seeing work as anything but hated and necessary toil and torture (travail) one of the biggest privileges out there? Don’t most people dream about the privilege of not having to work?
Setting aside Larry Summers’ considerations of whether ability corresponds with the number of female professors in STEM — which needs to be carefully worded for a reason, but, I agree, should not be off the table entirely — was a whole bunch of dumbspeak about how girls like girltoys and boys like boytoys. That doesn’t mean his entire point should be discarded, but it does explain, and justify, a lot of the mockery, because good god man, have you even really dipped your left pinky into the literature on this topic? is a viable response to anyone who thinks toys are an indicator of anything.
Let’s also not forget that plenty of people agreed with Summers, and depicted the whole situation as look, they’re martyring the Harvard president! This was very much a *controversy*, not a scandal.
So I know you want to assign low status to “thinking toys are an indicator of anything”, but I don’t know what’s your point against this.
oxyderces, your post is a mess.
4. And the nature side of same suggest that sex-specific mental differences only appear after puberty, once the adult balance of sex hormones has been established.
Hmm? I don’t get where this is coming from. Don’t sex hormones differ between prepubescent boys and girls too? What are the implications of, say, an experiment showing that chimpanzee infants, like human infants, show sex-specific toy preferences?
edit for clarity:
Why should the nature side of the nature-vs-nurture dichotomy naturally suggest that the only sex-specific differences are restricted to adults? Assuming, for generosity, that sex hormones are the only influence on sex-specific differences, then all I would conclude from knowing that sex hormone levels change over lifespan is that sex-specific differences probably also change over lifespan, not that differences can only appear once the process is “complete”.
And if it’s possible to detect male hormones in mothers who are pregnant with sons, at a greater level than is present in mothers who are pregnant with daughters, isn’t that sufficient to show differences in exposure to sex hormones pre-puberty?
(Sorry, I carry on too long in my comments, I guess.)
“Nature” would suggest that sex-specific differences are *stronger* after sexual maturity, at the least, and that’s enough for Scott’s argument.
“Why should the nature side of the nature-vs-nurture dichotomy naturally suggest that the only sex-specific differences are restricted to adults? Assuming, for generosity, that sex hormones are the only influence on sex-specific differences, then all I would conclude from knowing that sex hormone levels change over lifespan is that sex-specific differences probably also change over lifespan, not that differences can only appear once the process is “complete”.”
Think for example of other more obvious sex-specific differences like chest hair and deep voice. These mostly appear only after puberty.
As far as I can tell, the biggest problem is that the timing is wrong. I would expect the change around 14, but I think for mathematical ability to switch we’ve got to wait until like 17 or 18.
There were news stories a few years ago about a British study that found a correlation between relative length of the second and fourth fingers, which was apparently a marker for the balance of male/female hormones in utero, and relative math/verbal ability shown in the SAT. While some of the stories didn’t mention it, the SAT in question was not the U.S. Scholastic Aptitude Test but the British Standardized Assessment Test given at considerably younger ages—I think 7 and 11 from a quick Google.
I replicated some digit ratio results in the Less Wrong survey sample, but I couldn’t find that one.
One day I’ll double-check it, write it up at a little more length, and post them here.
Couldn’t it just be that older students tend to be taking harder math classes, and the least talented ones (disproportionately boys, given the higher-variance thing) will stop taking them* as soon as permitted? There could be some bell-curve-lopping going on even within high school.
*Assuming they’re allowed to. I technically didn’t have to take any math classes past 10th grade, which is roughly the age you’re talking about.
Speaking of surveys, whatever happened to the Slate Star Codex survey?
David, the SATs in England and Wales are designed to test how well the school has taught the national curriculum. The nearest thing to tests of innate ability for 11 year olds are the CATs or the reasoning tests for entrance to selective schools.
I believe it is plausible that there is an innate element of social ability in the English paper, but that is a different skill to verbal reasoning.
Looking at comments below, perhaps the US equivalent is that SATs in England and Wales are like a US grade, while UK CATs and reasoning for selective entrance are like a US IQ type test.
The bias/stereotype thing, I think (going on the push for ‘encourage more girls to take Honours Maths in school’ over here) is to do with exactly that:
(1) Perception that maths is really difficult and only the really smart can do it
(2) Perception that boys are smarter than girls or at least better than girls at maths
(3) Girls internalise these perceptions and don’t try for the higher level classes because they assume they don’t have the ability and will fail
(4) Whereas some girls, at least, do have the ability and would succeed except they’re convinced they’re not as good as boys because everyone knows boys are better than girls at maths
And round and round the mulberry bush we go, with girls not taking higher level classes and boys doing so, thus making it a self-fulfilling prophecy (at least, according to this reasoning) that boys do better than girls at maths and we can see this from the percentages of boys versus girls taking higher level classes.
“As far as I can tell, the biggest problem is that the timing is wrong. I would expect the change around 14, but I think for mathematical ability to switch we’ve got to wait until like 17 or 18.”
Alternative hypothesis- maybe the nature of math classes changes at around that age. In the standard American curriculum (with no grade skipping) that’s the age when you start learning calculus, and you have to think about things like infinities and some fairly tricky proofs. The early math classes are more or less just “here’s an algorithm: memorize it, and use it just like we taught you” which rewards hard work and discipline much more than aptitude. All of grade schools math is mostly just arithmetic, where there’s almost no room for any creativity. Calculus is the first level where you start needing some real aptitude to succeed.
My experience of calculus was that it was just about as algorithmic as everything that led up to it.
My experience with math was that it only really got hard in any way in university. With some exceptions, I was average to slightly above average in math but now I’m struggling. One of the topics later in school, stochastic, I did extremely well. Then again, I’m male, go me.
Taymon, differentiation is quite algorithmic, but integration isn’t. There isn’t any fixed algorithm for finding antiderivatives.
You don’t get asked to analytically integrate arbitrary expressions in basic calculus. You get asked to integrate expressions of a form that you learned an algorithm for integrating.
Mathematicians tend to classify calculus as “arithmetic” rather than “real math.”
Honestly, if you get an actual number out the end, it’s arithmetic and not real math.
My experience of math is that it is a lot like a gym class. Practicing it blindly helped me pass high school tests more than understanding it. Everything understanding related dissipated under the nervousness of the test. If it was committed into mechanical muscle memory, so to speak, how to solve equation type 1, 3, 3 etc. I could do it.
I got bad grades because I refused to practice it. I found it too boring. I think girls were more able to do force themselves to do things they find boring.
I think puberty simply made me restless and difficult to deal with the boredom of having to repeat solving the same equation 10 times to commit it to the “muscle memory” where I can do it automatically even if test nervousness makes me almost forget my name.
Taymon, I never went to any American school, so you’re probably right. Here in Germany high school calculus did indeed involve integration where finding the antiderivative required a bit of tinkering and not just rote application of algorithms.
> This seems to be based off of the AFAIK correct observation that high school girls get better grades but high school boys better standardized test scores (at least in math).
Yeah that’s it, I checked for standardized scores rather than grades.
TIMSS data (tw: rather large pdf) has U.S. fourth-grade boys performing significantly better than U.S. fourth-grade girls on mathematics assessments, although there’s no significant difference in such places as Serbia, Lithuania, and Taiwan. (There are large differences in favor of girls in a lot of Muslim countries; there’s at least one obvious potential explanation but I have no idea if it’s correct.) Unfortunately nobody seems to have reported differences in variance between the male and female populations, but someone could do it themselves if they really wanted.
Anyway, if fourth-grade boys really do perform better than fourth-grade girls on these tests, and if TIMSS is measuring something like ability rather than just regurgitated knowledge (I think it’s actually a combination of both), that would appear to falsify “the gender gap appears at puberty.” Or, at least, it would suggest that if the gender gap does appear at puberty, it’s at least partially manifested by girls getting worse at math — like actually worse, not just relative to pubescent boys, I think.
Help me out – what’s the obvious explanation for Muslim countries? Fewer girls in school there so more selective for the smartest?
That’s what I was thinking, yeah. The girls who go to school are much more likely to be children of wealthy, educated parents. I have no idea whether or not this is true, but it’s at least plausible.
(I also don’t know whether it explains Thailand.)
I would assume the explanation would be a variation of the same mechanism which has caused 70% of science & engineering students in Iran to be female.
“Fewer girls in school” doesn’t explain that. I don’t know what does but I’m going to assume it’s cultural.
So I grew up in Jordan, which has one of the bigger gaps in favor of girls, IIRC. Some thoughts:
The idea that different people are good at different things, or that you should do what you’re good at or otherwise love, is faint to nonexistent. Everybody has to take the same classes until the last two years of high school, at which point the smart kids (by overall GPA) are accepted to the science track, and the rest to the humanities track. Then you apply to university, where you don’t get to pick a major either: you’re admitted to one based on your grades. Medicine and engineering require the best grades, followed by I think pharmacy? Actual science is further down and things like economics, business, and law are very far down. Psychology is at the very bottom.
Anyway, what ends up happening is that everybody wants to be good at math, everybody is expected to be good at math, and girls (who learn to sit still and be good earlier than boys) end up doing better at math. Because (and I’m editorializing here) it’s not “boys are good at math” or “geniuses are good at math” or “anti-social androids are good at math”, but “smart people are good at math”.
I think y’all are underestimating how much room girls have to be discouraged from math and science in Western education systems, how much math and science departments actively try to discourage anyone who’s discourageable (e.g. “weed-out” courses, the genius myth, overstating publish-or-perish), and how much more that hurts girls than boys.
call_me_aka: Interesting stuff. Thanks.
I have to ask: Is that a trigger warning on large pdfs?
Or does tw stand for something else?
That is an ironic trigger warning on large pdfs.
Thank you for warning for the PDF, now I wish they were always warned.
Now that I’ve seen several people express the same sentiment, I’m curious: What is it about pdfs that’s bad and requires a warning? For me, the pdf is usually displayed in its own tab. Less often, my browser will want me to download it, or it won’t be accessible to me due to copyright, etc. Is my experience different from that of others?
In-browser pdf readers tend to override standard keyboard shortcuts, giving them different meanings. It’s very jarring.
And more specifically with large pdfs, mobile devices often choke on rendering them.
Not just large PDFs. Mobile devices just don’t have the oomph for PDF.js, so opening PDF on mobile will generally start a download, requiring an app switch to view the PDF. On devices with less memory (i.e., anything that isn’t less than 2 years old and a flagship), an app switch almost invariably causes web browser tabs to be evicted.
This was my reasoning. I’m not too proud to admit that I’ve spent a fair amount of time in my life browsing SSC comments on my phone.
Also, maybe someone has PTSD triggered by large PDFs. Can’t be too careful these days.
What I really love is the people who observe that girls get better grades and boys SAT scores and so declare the SAT biased against girls.
Nevermind that one is objective, one subjective; one knows the pupil’s sex, one doesn’t — don’t use Ockham’s Razor and say schools are biased against boys.
Schools seems to be biased (and increasingly so) against “male brains,” regardless of what kinds of bodies they’re in.
Is there data on grades and test scores for un-transitioned transgender highschoolers that shows the pattern for self-identified gender rather than apparent gender? Because that data set sounds really neat.
I’d worry about sample size. I’d also worry that you’ll be massively confounded by the prevalence of mental illness among the transgendered, which will tend to drive down test scores.
Wow, I didn’t realize anyone would take (what I now, in hindsight, realize is) the literal interpretation. No, I just meant girls who are more systematizing than emphasizing, disorganized, inattentive, and have a tendency to procrastinate/lose/forget to do their homework.
…need structure and assistance in developing better life skills, not easy As for being “so smart”.
Speaking from experience, this is true of boys as well.
I’m not sure anyone is advocating grades “for being smart.” I’m not really sure what point you’re making.
But, you did remind me of a comparison I read about elementary teachers in the U.S. and teachers in . . . Denmark (I think). If the Danish teachers had students who were bad at packing everything they needed into their backpacks at the end of the day, the teachers would quietly help those students.
The U.S. teachers wouldn’t. They figured, if other students can do it, then these others should, too. Why should I have to help?
I’ve been seeing the word “neurodiversity” a lot lately, and I can’t help but think that the Danish classroom is the better example of this concept.
@Anonymous
That doesn’t sound like advocating the Danish approach at all, because schools used to be even more hostile to disorganized/procrastinating/inattentive/neuroatypical kids in the past. Sorry if I misunderstood you.
@haishan, yes, that’s why I characterized it as having a “male brain” . . . because it’s more typical of boys.
@Nita, I’m not sure I understand you. I brought up “male brains” in reply to Mary, who said that schools (presumably, in the U.S.) are biased against boys. I’m arguing that they’re biased against certain traits that happen to be more common in boys, but occur in girls too.
You don’t think the Danish classroom in my example is more accommodating to neurodiverse students?
Here’s an article describing what I’m talking about (although it’s couched in terms of boys vs. girls).
Since you said that schools are increasingly biased against male brains, I thought you wanted to bring back some practices from the good old days — you know, things like corporal punishment or authoritarian teaching styles.
But if you’re advocating for a more supportive environment, I suppose you meant some more recent changes in schooling*, and I misunderstood you 🙂
* like… extra points for good handwriting? I’m not from the US, I’m not sure what goes on in your schools
@Anonymous
Thanks, that’s a good article.
On one hand, I agree that reducing a kid’s subject grade for being disorganized in unrelated things is completely wrong. We used to have separate weekly conscientiousness and behaviour grades back in elementary school.
On the other hand,
is such an odd thing to say. The grade might not reflect the student’s knowledge of the subject, but it does reflect their overall performance.
Teachers use grades to identify issues and track progress, so it makes sense that kids with conscientiousness issues / untreated ADHD would get lower grades. But I agree that these issues should be identified, addressed and tracked separately from subject knowledge.
Since you said that schools are increasingly biased against male brains, I thought you wanted to bring back some practices from the good old days
You know…now that I think about it, yes . . . but those practices would include sitting in desks in rows, working individually rather than in groups, being taught content systematically, etc. I know that people who teach math at the CC/lower undergrad levels are having to push back against mandates for graphing calculators. They also see the lack of graphing-by-hand as hurting student’s ability to pick up concepts.
…as opposed to being taught randomly? Is that a thing now?
All right, now I’m completely fascinated by American schools. What the hell goes on there? Why are grades considered different? My own far-distant days of education, we got grades on tests and homework.
We didn’t get points taken off for non-attendance or other things. We might lose points for illegible handwriting or sloppy work, but in general if you got 9 questions out of 10 right on a test, this was 90% and an A grade. There was, after all, only one right answer to a maths question or one correct spelling in an English test.
Certainly things like marking essays was more subjective; why did a teacher give a C+ or a B- for a particular essay?
But the way you lot are talking about grades versus standardised tests makes me think they have no relationship and I don’t understand that in the context of Irish education (our two big State exams are the Junior Certificate at age 15 and the Leaving Certificate at age 17-18. Grades get converted into points for college courses. Universities used to have their own entrance exam, the Matriculation, which ran in tandem with the Leaving Cert but these days it’s pretty much optional – your Leaving Cert points are what gets you on a course).
High school grades aren’t standardized in any way–a “B” at one school isn’t directly comparable in any way to a “B” at another school. Hell, the courses at one high school aren’t necessarily comparable to the courses at another.
Some states have some sort of standardized test you need to pass to graduate Xth grade, but it’s generally a “everyone should pass and we only report passing rates” sort of thing. It doesn’t like show up on resumes or anything.
The only thing comparable to, say, the British A-levels (I’m far more familiar with the British system than I am with the Irish) is the SAT II subject tests, run by the same company that does the SAT and the GRE. And most people don’t take most of those. I was applying to elite colleges so I took three.
Also possibly the AP tests, which are graded from 1-5, where a 3 is supposed to represent “would get a C in an average college class on this material.”
But all of those things are totally and completely unconnected to your high school grades, which are determined by your teacher however the hell your teacher decides, subject to whatever rules your school has.
Deiseach, homework is a big part of American high school grades, probably the majority.
Authoritarian teaching styles still make girls have better grades than boys. Source: grew up beyond the Iron Curtain. There was no corporal punishment, still just about every authoritarian aspect except for that. The idea was to force us to deal with the boredom of rote memorization, and girls generally obeyed, boys rebelled in all kinds of ways (such as not doing homework). ADHD diagnosis was not a think, we were simply called undisciplined. Girls were easier to bully/frighten by teachers.
I don’t know why young boys are supposed to be able to perform better under authoritarian styles. Testosterone makes it harder, not easier to put up with bullying from above, usually, it leads to a rebel-without-a-cause dynamic.
Analyzing the article, about the authoritarian style of Eastern Europe:
– Homework, as in, memorizing stuff for randomly selected oral exams every day, meant about 50% of the grade. Boys were marginally worse than girls in this because of not preparing every day however, boys were often good at bullshitting through it. It is possible to confuse a teacher into giving a C on an oral with zero preparation if you are smart and well-read and a good bullshitter. The teacher asks you about the development of literacy under Charlemagne and you don’t know this but you know it sucked before Charlemagne so you say “Well things got improved because” and here speak minutes of how dumb everybody was before. It made us excellent at bullshitting.
– we had midterm and similar written tests, and usually, especially if the random orals were bad, we were offered elective tests or orals near the end of the term to get a better grade, yes, this cramming worked better for boys
– in the rare cases written homework was graded girls were way better at it. Especially the reading journals for the summer break where were supposed to read some mandatory books and write long reviews. Girls worked on it all summer, boys the last 2 days. Yeah, that did not work out well.
The Educational Testing Service actually has done studies to track down the cause of women overperforming their SAT scores (alone) in grades: women have higher big 5 conscientiousness than men on average. Conscientiousness predicts hard work and grades in both men and women, as well as later success.
If you match on both SAT score and conscientiousness the underprediction/overprediction largely goes away.
That’s why you want measures of both cognitive ability and personality in admissions/hiring. And it supports the view that an excessive weighting on SAT scores relative to hard work could relatively favor men, although an optimal predictive algorithm would use both.
My impression of the general population is that *everyone* thinks school is biased against boys. Almost all children (boys and girls – I’ve asked middle school kids of both genders) believe that, and many adults believe that at well.
Whereas, most people are not even aware that boys do better on the standardized tests.
)cont) Although, most people are not cognizant enough to distinguish between male behavior and active discrimination unless prompted.
This might be a conflict between opinions of the public and politics/media. President Obama was quoted calling boys doing worse at school “a great accomplishment”.
I don’t like that explanation. I think it’s simpler to proffer that grades and SAT scores are not measuring the same thing.
Because the vast majority of high schools do not teach math, they teach calculation. These are related topics, but they require vastly different skills. For more on this, see [1].
As far as the rest of the post goes, Scott forgets that “there are no difference whatsoever in male and female intelligence” is an axiom, though some school of thoughts (Harvard) actually derive it using a proof by termination.
[1] https://www.maa.org/external_archive/devlin/LockhartsLament.pdf
Why do you believe that you can argue using evidence with people who bellyfeel blackwhite doublethink doubleplusgood?
I don’t think you actually understand what’s at stake.
The entire objective of the gender gap exercise is to conquer STEM for the party. It’s the only remaining part of academia which harbors thoughtcrime due to its oldthinkful insistence on evidence that cannot be rectified to goodthink.
If they succeed, you will go to a joycamp until you learn to love Big Brother. Lysenkoism will be back, and humankind will enter a dark age.
I think this is a conversation we all desperately need to have.
We get it. You read Nineteen Eighty-Four. This is not a substitute for actual argument.
Agreed; it’s sad that so many people have read it and not the virtual companion piece “Politics and the English Language”, which screams at the reader not to write with stilted cliches and tribal loyalty markers.
And asserts that the passive voice is used too much.
The people at Language Log have an impressive rant against Politics and The English Language; still, I think there are some things in there which survive. The interesting one here is The Prevention of Literature, as (among other things) it explicitly addresses STEM types. Before we get too smug, it basically accuses our forebears of not noticing what’s going on, and that we’ll be in for a rude awakening if then-present trends continued.
“The entire objective of the gender gap exercise is to conquer STEM for the party.”
My understanding is that STEM academics are generally left-of-center already, so not much reason for “the party” to need to conquer.
“My understanding is that STEM academics are generally left-of-center already, so not much reason for “the party” to need to conquer.”
No, STEM professors’ political affiliations roughly match the general population, about 50-50. Humanities professors are more like 80% left. Nancy Hopkins’ own MIT is notable for how conservative it’s faculty is relative to other universities in the Boston area. It’s also almost entirely STEM focused.
“No, STEM professors’ political affiliations roughly match the general population, about 50-50.”
This is false. See http://www.people-press.org/2009/07/09/section-4-scientists-politics-and-religion/
Note the single digit figures for republican membership in the “Party Affiliation among Scientists” table.
I don’t think party affiliation tells the whole story; the “Party” Anonymous mentioned is not necessarily an actual political party. (Especially not a party in the US, where all philosophies must fall into one of two boxes in order to count.)
I’ve voted for Democrats all my life, I describe myself as liberal on the conservative-moderate-liberal scale, but I identify much more with the “gray tribe” than the “blue tribe”, and I don’t see much value in the social justice ideology that so many other liberals are so gung-ho about. There’s a political division there, and I think Anonymous may be right that that division has contributed to the focus on beating gray-tribe-affiliated fields with the social justice stick.
What makes you think there is not an actual argument there?
The 1984 references aren’t superfluous; they’re used to denote the concepts that 1984 was written to explain.
Because his entire argument is references to 1984, without explaining any of the essence behind the symbolism. In essence, he’s using the book as a rhetorical banner, like so many others do, in a reductio ad Orwellium.
A staunch left-wing ideologue would say essentially the same thing, except with different examples (say, climate science, sex ed as opposed to abstinence-only, and a general conservatives-dismiss-government-funded-solutions thing like universal government-funded healthcare).
It equivocates between different groups that don’t all think the same. A given conservative doesn’t necessarily believe in abstinence-only sex ed. They might object to particular government-driven solutions to climate change without contesting the science, or take a principled stand on letting the science do its thing, even if they disagree, and so on. Similarly, just because someone is left of centre doesn’t mean they think that the gender-gap in STEM subjects is because of sexism at the top, or that posts like Scott’s should be suppressed. In fact, I suspect the subset that think posts like Scott’s should be suppressed is miniscule (the proportion that writes angry not-quite-on-the-mark rebuttals is not the same thing).
You are being tribal. Stop it.
To me, it looks like you couldn’t say the same thing with those examples.
I’d love to be proved wrong though.
This isn’t quite an identical claim, but I think it’s similar enough to be demonstrative. I also want to be clear that while I am generally left-of-centre, this is just an exercise in demonstrating what a roughly-equivalent opposite-tribe rant looks like:
“Why do you believe you can argue with conservatives using facts?
I don’t believe you understand what’s at stake.
The objective of global warming denialism is just to muddy the waters of public discourse, delaying action on global warming as long as possible, so oil companies can get as much profit as they can. They don’t care about the future generations that will have to pay the price – they’ve got theirs.
They’ll do whatever they can to suppress actual research into climate – see Ted Cruz being put in charge of NASA, the way they go after individual scientists with accusations of fraud, see Inhofe.
I think this is a conversation we desperately need to have”
For bonus points, reference Murdoch and News Corp – they’re probably the best direct replacement for the ‘academia is full of ideological left-wing views’ meme.
For sex ed, the complaint would be similar in style but not in form – you’d accuse Conservatives of Hating Women and wanting sex to be dangerous/difficult/risking pregnancy to Punish Them. The stylistic similarity is accusing people of claiming to hold beliefs and positions as part of a conspiracy to do something nefarious, rather than because they’re honest beliefs.
Government-funded solutions, the accusation is that Conservatives in government do their best to hinder such services when they exist by cutting their funding, and then they claim that the poor performance of a service they’ve gutted is due to government incompetence rather than a bevy of cuts and so try to privatise it. Then they reduce taxes so more services need funding cut… That one is more applicable outside of the US where there’s more government-funded healthcare/education/unemployment/etc. services though.
James Picune is right on the mark – I’ve seen nearly identical constructions on Daily Kos over the years. Less so recently, they’ve gotten a bit more bubble-universe, but it’s still there.
James, that was positively eerie. Well played.
“I suspect the subset that think posts like Scott’s should be suppressed is miniscule”
And the Inner Party was a minuscule subset of Oceania’s population. You’re not exactly refuting the analogy. Whether the people calling for Larry Summers to lose his job were a large faction, or minuscule, isn’t really important; either way, they got what they wanted.
PS there’s a “minus” in minuscule”.
It is important if you’re trying to blame ‘the Left’ rather than that particular subset of the left. Anonymous is using bad behaviour by a group of people who are left of centre to tar all left-of-centre people. At least, assuming this is the same anonymous who talked about Marxist kafkatraps in response to Grey Enlightenment talking about how ‘the Left’ shouted down Larry Summers.
And huh, I’ve probably been spelling that word wrong for years.
I don’t see how one can conclude that all left-of-center people are being tarred.
I understand the benefits of avoiding tribal signaling. But I also see a paradox, that it’s important to talk honestly about data on gender differences in the distribution of verbal and mathematicL ability, but it’s not ok to Talk honestly about the fascist elements of thought police in academia, which is a prominent feature of the left today? How can we fight this scourge if it is taboo to mention it directly?
Indeed, the most interesting thing about the Summers/Hopkins incident is that they are both leftists. Even party members are subject to the thought police. The origins and tactics of the thought police are not a parochial issue of tribal signaling.
I don’t object to complaining about, for example, the social justice movement’s tendency to make disagreeing with it about anything a moral failing.
What I object to is making it at “The Left”. It’s a noncentral argument. There’s substantially more to left-wing politics than social justice. Be more specific and you’re less likely to activate a broad-spectrum tribal response.
If you’re thinking “Oh but this is a feature present in nearly all of left wing politics!” maybe you should consider exactly how mirror-universe you is right now talking about the Fascist Elements of Right Wing Politics. It’s not hard to write rants like this. The left-wing one would go on about how the most extreme elements of the right enforce doctrinal purity in the party, preventing any kind of bipartisanship and refusing good ideas just because they originated in something generally considered Left. Or it would talk about abuse of science for political ends. Or vote suppression and gerrymandering.
I’m sure you’re not in favour of enforcing doctrinal purity, abuse of science, or gerrymandering. But it’s really easy to construct a rant claiming that the Right is totally for those things, by eliding differences between subgroups and focusing on specific areas or examples and then overgeneralising.
“I don’t object to complaining about, for example, the social justice movement’s tendency to make disagreeing with it about anything a moral failing.”
Seriously? You’re whining about other people’s “noncentral” arguments, and arrogantly telling them to “stop it”, while referring to “treating disagreeing with it about anything a moral failing” a central feature of social justice. Did Gandhi treat disagreeing with him about anything as a moral failing?
There is a cluster of behavior that many people think deserves discussion, and which they therefore need a term for. Some people use the word “liberals”, some people use “the Left”. You use “social justice”, and treat the use of anything else as a moral failing, while hypocritically accusing other people of being “tribal”.
The Left Wing is not the same as left-of-center. I don’t need to imagine some mirror universe of myself; I criticize both the Left and Right Wing.
One issue; left and Left. I’ve noticed that when people talk about the Left, they tend to mean people left of whichever mainstream[1] party in a given country is leftmost – i.e. excluding the centre-left. Whereas I tend to see people using the lowercase ‘left’ to include the centre-left. However, other people might quite reasonably say, “Argh! What a stupid thing to hang on a capital letter” and I can’t argue with them, and if they go and read the two interchangeably, well, people who write should be clear.
[1] As in, gets in to power nationally from time to time.
“The Left Wing is not the same as left-of-center.”
I was interpreting those two as synonymous. Maybe it’s a cultural thing, but when I see people talking about ‘the Left’ or ‘the left’ or ‘liberals’ (although that term isn’t really used where I live), they tend to be using it to mean ‘the kind of people who vote for Local Left Of Centre Party’ – so about 50% of the population. If Anonymous and Grey Enlightenment above don’t mean that, then I have less beef with it.
Pingback: Perceptions Of Required Ability Act As A Proxy For Actual Required Ability In Explaining The Gender Gap | Slate Star Codex | Witti blockt
The average man gets 154.3 ± 8.6 on GRE Quantitative. The average woman gets 149.4 ± 8.1. So the threshold for Mathematics admission is 7.7 points ahead of the average male test-taker, or 0.9 male standard deviation units. This same threshold is 12.6 points ahead of the average female test-taker, or 1.55 female standard deviation units.
Careful now, Larry Summers got run out of the President’s office at Harvard for suggesting that this thought experiment be performed.
Larry Summers got in trouble for talking about variance. I’m not sure how variance relates to tests like the GRE, which show large differences in mean but relatively small differences (albeit in the expected direction) in variance.
Part of the problem is that the tests lop off the bottom X% of the distribution because you’ve got to be pretty smart to take the GRE. I’m not sure I have all the numbers I would need to check if that matches a variability hypothesis.
Really, now, do you think he would have been treated any better if he had talked about the mean rather than the variance? If anything, it would have been worse: if the genders (or races, etc.) have the same mean intelligence but greater variance, then you can rescue at least one interpretation of the axiom that there is no difference in intelligence between them. If the mean is different, then it’s basically game over.
Disagree that 8.6 vs. 8.1 is small in a restricted sample, because of the multiplicative effects and how quickly the tail of the exponential distribution dies off. That’s a significant difference that does have a large impact on the number of men vs. women we would expect in roles of extreme competence.
“you’ve got to be pretty smart to take the GRE”
As I mentioned below, a big chunk of GRE takers aren’t “pretty smart” compared to all college graduates, but 50% or lower. There are many, many “really smart” people who would never take the GRE. Some because they’re taking the LSAT, GMAT, or MCAT, but many because they just never go to grad school.
This is, of course, true for the other grad school tests, but the difference is that some of the largest grad school programs are pulling in almost exclusively average to lower than average scorers.
You might want to remember, too, that there are lots of colleges filled with people who got lower than 500 on every section of the SAT, most of them not white, and they are under pressure to graduate students.
That’s a big problem with ignoring race in these sorts of analyses. You get a skew not just because of affirmative action, but because blacks, Hispanics, and even Asians with lower SAT scores are encouraged to go to college while whites with same are not–particularly white males, who have a fairly wide range of respected occupations that do require brains and don’t require college to choose from: military, law enforcement, fire fighting.
Meanwhile, all sorts of female occupations require an AA or BA–nursing, teaching, cosmetology, social work–and have their own grad school programs but don’t require anything extraordinary in brains.
So the assumption that there’s a sort of cognitive stratification going on is *mostly* valid, but not completely, and definitely not when combining race and nationality.
That’s a huge oversimplification, there are 2 scandals associated with Larry Summers at Harvard.
Scandal 1: Larry Summers makes his remarks about ability-based differences causing gender disparity.
http://en.wikipedia.org/wiki/Lawrence_Summers#Differences_between_the_sexes
Scandal 2: Larry Summer’s associate Andrei Shleifer (Harvard professor) commits fraud.
http://en.wikipedia.org/wiki/Lawrence_Summers#Support_of_economist_Andrei_Shleifer
It’s not certain which of the scandals led Summers to resign, but the fact is the peak of the uproar over Summers’ gender comments was in the summer of 2005 and the peak of the uproar over Andrei Schleifer was in Jan 2006 and Summers resigned in Feb 2006.
Interesting. Hadn’t heard that.
Thank you.
The timing coincidence of peak Schleifer and the resignation is reverse causality. The magazine article chose its publication date to match a faculty meeting where he was going to be attacked anyhow. Of course, it made this choice because it hoped to achieve some forward causality, and it probably did.
(I do believe that the Schleifer scandal played more of a role than any other scandal, I just reject the timing argument for that claim. But I am also concerned about restricting to scandals reported outside of Harvard. Internal politics played a huge role in his downfall.)
Beware ecological correlations
A note: Would you mind fixing the arXiv link to point to the abstract instead of directly to the PDF? From the abstract you can click through to the PDF; not so the reverse. And from the abstract you can get e.g. other versions of the paper or other papers by the same authors, etc.
Thank you!
…maybe I shouldn’t have said that, in fixing this you broke the link with an extra quote mark… (but thank you for fixing it).
LINKS ARE HARD.
Let’s go shopping!
I think you are weakmanning objection #3. There are more ways than the first-order testing effect of stereotype threat in which GRE Quantitative could fail to be a measure of innate ability. For one thing, it is at least in some part a measure of effective preparation over years of education, and it could be that women are disproportionately socially discouraged away from that preparation. For another, the GRE test taker population is self selected, and it may be that women of high mathematical ability disproportionately decide not to take it, perhaps discouraged by a perception that the fields in which they would like to pursue graduate study are unwelcoming to women.
For the specific case of computer science, I would be interested in your comments on _Unlocking the Clubhouse_, which is still one of the classics on women’s experiences in that field, and an interesting read just as a piece of sociology.
” There are more ways than the first-order testing effect of stereotype threat in which GRE Quantitative could fail to be a measure of innate ability. For one thing, it is at least in some part a measure of effective preparation over years of education, and it could be that women are disproportionately socially discouraged away from that preparation. ”
This was the second objection I mentioned, the one I analyzed SAT scores to try to divert.
“For another, the GRE test taker population is self selected, and it may be that women of high mathematical ability disproportionately decide not to take it, perhaps discouraged by a perception that the fields in which they would like to pursue graduate study are unwelcoming to women.”
The GRE gap is identical to the SAT gap, and nearly everyone of high ability takes the SAT.
Fair points, but I think you underestimate the degree to which SAT scores may reflect differential preparation. Taking the same classes is not the same thing as having access to the same effectiveness of preparation, especially if teachers and classmates treat mathematically inclined girls differently.
Also, dropout rates may not, as you suggest, simply reflect difficulty of the material; they may also reflect difficulty of the social environment. The latter may disproportionately cause students of higher ability to exit, since they will have more other good options, so may be less inclined to put up with the bullshit.
Differential preparation doesn’t really affect SAT scores much. In fact, even when we actually compare highly-prepared to unprepared people, the math gap still isn’t as big as the observed gender gap.
But I’m not talking about preparation in the sense of coaching focused on the test; I’m talking about preparation in the sense of general K-12 mathematical education.
It’s not super clear to me why specifically targeted SAT preparation wouldn’t work, but classes that have nothing to do with the SAT would.
The SAT tries to be a sneaky IQ test. To the extent that it succeeds, training – beyond a very low level of “has learned what reasoning is and is accustomed to it” shouldn’t help too much.
[replying to your subsequent comment, not sure why it won’t let me do so directly]
I agree that much of the SAT tries to be a sneaky IQ test. I think the Math part, on which you’re hanging your hat here, probably mostly fails at this. Facility with algebra, for example, depends very much on having been taught it *well*, as those of us who were taught it both badly and well at different times can attest. There have certainly been people who could reason their way through algebraic concepts without any real preparation in it– otherwise we wouldn’t have algebra in the first place– but such people are very, very rare and unlikely to show up in aggregate testing stats.
As someone who took around 12 Standardized tests (SAT, PSAT, ACT) in Highschool, and the GRE later, I can say a few things.
The SAT Math section does not test on any mathematical concepts beyond what is normally termed ‘Geometry’ which is normally a 10th grade (or prior) math course, and is required for every student to take in every part of the country.
The GRE Quantitative section does not test on any material presented between 10th grade and the end of college.
You can see sample versions of GRE quantitative questions here. http://www.majortests.com/gre/problem_solving.php
You will notice straight-line slopes, logical concepts, fractions, exponents, quadratic equations, circles and simple geometric relations. There are no logarithms, complex exponential, limits, or even rudimentary calculus, or conic sections. You can forget about Linear Algebra, optimization, statistics, or Differential equations.
So, in short, the SAT tests only on Mathematics that every girl is in fact told she is REQUIRED to take. Which has to count as some form of a positive signal of encouragement and expectation that they are capable of performing in this subject.
Secondly, taking the GRE quantitative is taking a test with identical subject matter, albeit a slightly different format, 4 to 6 years later. For a girl who has made it through a college B.S. program and intends on some form of graduate school, I find it very suspect to assume that 6 years is insufficient test-prep time to overcome micro-aggressive dissuasion suffered during middle-school.
Just my 2 cents. Also Scott, that should help raise your confidence in the SAT/GRE correlation. They are literally the same test, with the same subject matter and same caliber of questions, albeit in a slightly different format.
It’s been a while, but I also recall the math in the GRE not being much different from the SAT / PSAT math.
It’s not true that nearly everyone of high ability takes the SAT, although that’s often assumed by coastal types where everyone smart really does take the SAT. Whole swathes of the middle of the country are much more focused on the ACT, so there are lots of smart students who don’t even think about the SAT unless they’re interested in a coastal university.
This causes problems for researchers who forget about the ACT and, say, estimate Iowans IQ to be 76. http://isteve.blogspot.com/2008/09/iq-and-wealth-of-states.html
Okay, good point, but it looks (very preliminary?) like the ACT gap = the SAT gap = the GRE gap.
In that case we could just collapse SAT + ACT into one exam and pretend everyone takes it? Maybe?
I think that it is best to just ignore the problem. Unless you do something like Kanazawa did that highly relies on the assumption, it shouldn’t matter. Both the SAT and ACT are biased because certain types of ambitious people take both. These people probably skew male and smart. (At least that’s true of the midwesterners who take SAT. ACT numbers used to be good because coastal people just didn’t take it. But now some do and I’m not sure about their demographics.) But I think that they are rare enough to not make a difference. If you really want to deal with this issue, you should probably restrict to a California, because everyone in CA who takes ACT also takes SAT.
Actually, I think more women than men take the SAT.
Yes, people who take SAT or ACT are majority female. But people who take both are probably male.
I’m talking about the problem Brett mentioned: the people who take both SAT and ACT are special. If you combine the data, you double count these people. If you just look at SAT or ACT, you are effectively double counting this demographic.
What is this demographic? Mainly, it’s selected for ambition. It’s probably smart and male. Double-counting it makes the high tail look male. But it’s probably a small demographic and it probably doesn’t matter, unless you do something crazy like Kanazawa.
The best standardized test would be one where preparation has a minimal impact on scores. There has been a recent push to make the SAT less like an IQ test and more like a knowledge assessment test ,and this benefits those who have the most money and time to cram.
Cite?
they keep making the test easier, for example by getting rid of the notoriously hard analogies sections
but are the hard sections ones that 1) predict something useful in terms of college/grad school success and 2) resistant to preparation? or is it just that the rich kid who can hire the very best tutors is going to do better than the kids who are stuck in bargain online prep courses?
Also, I believe the GRE just revised to make the test harder, particularly in the quantitative section, because too many people were getting perfect or near-perfect scores.
Analogies satisfy both, being both a predictor of learnedness and are hard to ‘game’. There are thousands of words to choose from and each word has a specific meaning, unlike math concepts, which tend to be fungible and interchangeable, of which there are fewer total math concepts to learn than number of words to memorize. Matrix tests would probably be ideal
that sounds plausible, but what I’m really looking for is data to support both of those points.
Also, I’ll add that I agree with you that the best test, from an equal opportunity perspective, is one that studying/preparing as no or minimal effect on. From the perspective of graduate schools though, they want tests that predict success in graduate school. Designing tests that 1) Predict grad school success in a variety of disciplines and 2) Aren’t influenced by how much time and money you can put into preparing sounds like a tall order.
And 3) willingness to devote extra time and resources to the things critical to one’s success in one endeavor, is predictive of one’s likelihood of success in other endeavors. It may not be fair that Dick can and will hire a private tutor for the classes he is struggling with while Jane can’t or won’t, but if I’m trying to allocate scarce resources to students marginally likely to complete a course of study in Math or Physics, that’s probably something I am going to want to know.
Balancing the SAT or GRE so the effect of differential test preparation accurately reflects the effect of similar efforts over an academic degree program would be a hard thing to do, and I make no claim that the tests are particularly accurate in this regard. But it is something you’d want to be able to test for if you could, so you might not want to design a test wholly indifferent to preparation.
Both the SAT and the ACT are extensively controlled for such bias as cram and prep, as well as racial/sex/culture. And they have been for decades. There was a period of time when ACT/SAT prep was a really effective thing, but the testmakers learned from it and now primarily those courses teach you how to be a good test-taker, including basic advice like “get a good night’s sleep the night before” to more tactical like ” since you’re time limited skip over questions you don’t know right away and go back to them after you’ve taken care of the ones you know.” The change really came when computer statistical analysis and reporting became inexpensive and easy and so you could actually find the problems. People forget what life was like before computers.
I worked with test administrators staticians and psychometricians for almost two decades.
http://web.stanford.edu/dept/psychology/cgi-bin/drupalm/system/files/cdweckmathgift.pdf
Relevant. There is a mechanism other than innate ability here which kicks in before high school. I’m predisposed to favor this explanation because it fits with my own experience. But I don’t think it will be to Scott’s taste.
Also a question about the data, which I don’t think makes a huge difference to the point but I’d like to know the answer. The paper uses GRE data on “PhD candidates.” As best I can tell, Scott’s data is on all aspiring graduate students. Those seem like very different samples to me, but maybe I’m misunderstanding the terminology used by American universities?
Definitely different at this math department in America; candidacy means having passed quals (written tests in several areas), found an advisor, and passed prelims (an oral exam on material that will be relevant to your thesis). I get the impression we have the meaning of “quals” and “prelims” swapped compared to many other universities, but that’s not really relevant to this.
The paper does not use the word “candidates” at all, let alone in the GRE section. It uses the word “applicants,” just like Scott. Moreover, the bibliography identifies the source as “Educational Testing Service, GRE: Guide to the Use of Scores (ETS, Princeton, NJ, 2012),” which is the same title that Scott links to. Except that he used a more recent edition. The paper probably used this one.
AUGH. Sorry to be misleading, my bad!
To me there is a big difference between an applicant for a PhD and an applicant for grad school. Don’t you all have Masters degrees? And Scott’s data seems to be about general grad school. (Yes I know it’s same source different year. Sometimes people publish different selections of datasets in these things.)
So is there a difference or not?
In academic hard sciences like math and physics, the master’s degree is usually a consolation prize for people who tried for a Ph.D. and failed – there are insufficient career opportunities at the MS level for very many people to explicitly seek that degree. Applied sciences and engineering, yes, the Masters->Industry career track often dominates Doctorate->Academia. I think some of the soft sciences follow this pattern as well, but I’m less certain there.
I’ve looked at the ETS numbers for both years, and they’re pretty much the same.
ETS doesn’t say “PhD” anywhere. I think that the paper is wrong to use it. I can reconstruct the GRE column in the supplement from the ETS data, so I know that they are not using some secret hidden source that’s only “PhD applicants,” whatever that even means.
Thank you, that seems conclusive. Thanks to the people who educated me about American grad school also!
“the perceived smoking correlation is just the actual smoking correlation plus some noise resulting from misperceptions”
A bit of noise won’t hurt you too bad as long as your sample size is good. It’s systematic bias that will get you every time. In this case, you may be inclined to answer that your social smoker friend Annie is “not a smoker”. But your social smoker friend Betty was unlucky enough to get lung cancer. You definitely think of her as a smoker – even though she never smoked any more than Annie. So it’s not impossible that “perception of being a smoker” would correlate even better with lung cancer than “actually being a smoker”.
“Noise” in this context refers to factors other than the two variables whose correlation is being studied. Larger sample size doesn’t get rid of it.
One more way in which your GRE-based calculation sort-of cheats: a department that’s aiming for an average GRE of 162 would have to set its threshold GRE not at 162 but at some lower number that I could probably work out if I were better at this sort of thing. Your calculation still illustrates the principle pretty well.
Regarding footnote 7, the study you link to is just a study of California.
I know, I can’t find anything else.
Warning to those interested in an academic career. Stay away from this topic.
Why?
Leslie, et al didn’t and those were sufficient to get published and actually to earn fame.
Don’t avoid the topic – just invent results that “everyone” already knows are true.
Bet you never heard of the 300 other social scientists who “stayed away” from the topic because they were unwilling to exploit crime stop to such a shameless extent and publish something with a giant hole in the logic that can only be uncovered by committing crime think?
[Retracted]
The problem of stifling conformity in academia is truly massive, and goes far beyond individual politicized issues such as gender and STEM. In essence, the modern research academy is a gigantic game of “Survivor”: entrants spend years learning how to pass a “peer review” process that ruthlessly roots out anyone unwilling or unable to navigate the elaborate structure of cliques and alliances that rules the roost in each discipline. They then embark on a career during which their every professional act will be judged by the same peer review process–including, for example, their casual social behavior, under the label, “collegiality”. And even if they receive tenure, which in theory guarantees them a job for life, their continued receipt of the real currency of the academic world–grants, awards, promotions, and so on–will still depend on their continued ability to navigate academic politics successfully.
The result is obvious in every field: research that is overwhelmingly of zero value to the world at large, but of great political significance within the narrow world its authors inhabit. It is evaluated based on whom it cites and credits, whose research it supports or justifies, and how much opportunity it provides for follow-up research from friendly researchers. Whether it is correct or remotely useful is, at best, a tertiary consideration.
Yes, one aspect of this deeply dysfunctional system is that academic conformity in many areas encompasses a brand of political conformity as well. But that’s merely a symptom, rather than a cause, of the underlying sickness. Until the ironclad rule of “peer review” is broken, and academic research is exposed to sane evaluation from outside as well as from within, we shouldn’t expect any improvement.
Thank you, I’ve never heard this so we’ll analyzed. Very illuminating
“research that is overwhelmingly of zero value to the world at large.”
The standard counterargument is that even if a professor’s research is useless, it helps make him a better teacher if for no other reason than by giving him writing practice.
I feel like Dan Simon’s post is overstating its points, based on my own experiences in Comp Sci academia. But then again, CS is a very industrially applicable field, which keeps us honest and focused.
Actually, my own perspective is also based on Comp Sci academia, and reinforced by my subsequent industrial experience. Here’s another, similar take:
http://crypto.junod.info/2013/09/09/an-aspiring-scientists-frustration-with-modern-day-academia-a-resignation/
Here’s a paper with very nice graphs about trends in gender and ethnic gaps on the GRE over time. There’s little change in the gender gap since the early 1980s, but meanwhile female representation in STEM fields has risen sharply. The standard deviations of both verbal and quantitative tests were larger in males in all years for which data were available.
This study based on large IQ standardization samples found males to have 20-60% percent larger variances in latent fluid, quantitative, and figural reasoning abilities.
There’s a recent meta-analysis of the effect of stereotype threat on the male-female gap on math, science and spatial skills tests. The overall effect size was g=-0.22 (i.e., -0.22 SDs), confirming the effect, but there were strong signs of publication bias. They estimated that if the studies apparently missing from the funnel plot had been published and were available, the effect size would have been -0.07, which is not significantly different from zero.
“There’s little change in the gender gap since the early 1980s, but meanwhile female representation in STEM fields has risen sharply. ”
What? How does that match with eg Mertz’s findings that the m:f ratio at the highest levels has gone from 13:1 to 2.8:1 since the 80s? Or is this getting hidden in mean vs. top-echelon type issues?
There isn’t any good evidence that the m/f variance ratio has decreased. Some evidence even shows that it has gotten continuously larger. http://www.sciencedirect.com/science/article/pii/S0160289613000457. SAT has been continuously dumbed down and has a very low ceiling. No representative sample either. Not a very good test for detecting changes in variance, but great for Hyde and Mertz type propaganda. Other tests like PISA also have a very low ceiling so pointing to them as evidence against the biological m/f variance hypothesis is silly. But that sure won’t stop Janet Hyde!
See also:
https://westhunt.wordpress.com/2013/02/26/narrow-distribution/#comment-10320
Yes, changes in the tail wouldn’t necessarily show up in the means. Also, it’s difficult to disentangle changes in the m:f ratio from changes in the tests themselves.
It was 17 to 1 for Caucasians and 4 to 1 for Asians. Since then the number of students getting selected has risen by a magnitude, though the ratio has remained flat since the early 90s in Jonathan Wai’s analysis of DUKE Tip to about 4 to 1.
I’m not sure what you mean by equating “SAT and GRE math tests are not reflective of women’s true mathematical ability” and “Argument from Stereotype Threat”. Certainly there are possible causes of a test/ability mismatch that don’t depend on perceived stereotyping.
E.absurd.g. the land of gender utopia eliminates virtually all sexism and absolutely all public perception of sexism – but the local equivalent of the math SAT includes a bunch of questions derived from American-rules football scoring that male students are much more likely than female to breeze through on account of having seen those exact problems solved repeatedly on ESPN. No stereotype threat, because everybody believes the test is fair and the girls are smart, but the boys get higher scores than they deserve and are tracked into physics and math careers more than they should be.
Possibly the mathematical measures that rule out stereotype threats also rule out other sorts of systemic gender bias in testing. If so, that should probably be more clear. Because if I’m the person assigned by the Matriarchy to poke holes in your analysis, this is where I would start. And I’d wager that the holes I would wind up poking, even if objectively minor, would be perceived by everyone not already charitably inclined as having destroyed, debunked, and eviscerated the entire piece.
Everything else depends on the SAT/GRE being accurate and gender-neutral. That point maybe deserves more than two paragraphs of defense on a single front.
Yes, the point deserves more than two paragraphs. It deserves a 1000 page book. That book is called The Bell Curve.
As it turns out, asserting that test scores accurately measure innate ability and defending this with “…as shown in The Bell Curve, the end”, does not increase the perceived strength of the argument among anyone who didn’t already agree with you at the outset. Murray and Herrnstein did a fair job of addressing that question, and bundled it with some other material that (fairly or otherwise) causes the whole thing to be widely dismissed as “Bell Curve = Wrong and Evil, and all derived from it is the fruit of a poisoned tree”.
We need a work that robustly addresses the test vs. ability question and refrains from any conclusions, prescriptions, or even implications beyond that point. Linking to that work, if it exists, would greatly strengthen Scott’s analysis here.
Maybe 10 years ago, a friend of mine suggested Linda Gottfredson for this purpose, saying what a great job she had done studying IQ and avoiding scandal. So I googled her and most of the top hits were hit pieces. (But that isn’t true today!)
As I remember The Bell Curve, it is surprisingly silent on IQ differences between the genders. The common observation that for male and female IQs the average is close to equal but the variance is higher on the male side, gets just one paragraph in the entire book, with hardly any mention of the many interesting consequences which directly follow from it (such as that in more IQ-demanding professions you’d expect to see fewer women, without that indicating an unfair bias in the hiring process).
In fact, I just checked the index and there is only one entry for Gender, which points to a single paragraph, mentioning the fact that men outnumber women on both extremes of the distribution only in passing.
The American Psychology Association report on intelligence would make much more sense:
http://en.wikipedia.org/wiki/Intelligence:_Knowns_and_Unknowns
Well, what would it mean for a pretty abstract math test to be gender-biased, in a way that doesn’t mean women are worse at abstract math?
Like, your football scoring example is kind of a reductio ad absurdum, and I’m not sure how it could possibly apply to things along the lines of “x^2 = 9, solve for x”. The closest I could come would be to say men and women are good at different kinds of math and the test focuses on the kind men are good at, but then you’ve granted the major premise that men and women are good at different things and you don’t have much cover from the people saying “Well, maybe the skills men are good at are the ones necessary for the fields where men achieve disproportionate success.”
Well, first, the Math SAT isn’t entirely abstract. Consider
Helpers are needed to prepare for the fete. Each helper can make either 2 large cakes per hour, or 35 small cakes per hour. The kitchen is available for 3 hours and 20 large cakes and 700 small cakes are needed. How many helpers are required?
and
Soldiers are needed to repel an attack Each soldier can fire either 2 cannon shots per hour, or 35 musket shots per hour. The battle will last for 3 hours and 20 cannon shots and 700 musket shots are needed. How many soldiers are required?
One of these is, per quick googling, an actual practice question. The other just as well could be. They both reduce to the same equation, yet I would expect girls to do slightly better than boys on the first version while the boys would do better on the second. Or, perhaps, take more/less time to get results of similar accuracy, which will still affect the total score in a timed test. And if the tests were written primarily by men who weren’t making an effort towards gender-neutrality, I’d expect to see more questions of the second sort.
Second, if men and women are good at different things, it does not follow that the skills the SAT and GRE cover are the skills necessary for the fields where men excel. They could be, but they could just as easily not. The stereotype you note earlier, that boys are smarter but girls are harder-working, could be correct. A few hours of testing may be good for measuring smartness, but does not reward hard work – anybody can put in three solid hours when their professional future is at stake. But actual achievement in a career or course of study in math or physics, could depend more on hard work than smartness. And if the college math and physics departments don’t accept the hard-working women because they didn’t do so well on the math SAT and GRE, we’d never see this[*].
I do believe that the SAT and GRE are reasonably good predictors of academic success in their relevant domains, and I do not believe that either are subject to gender bias via e.g. gratuitous football- or artillery-related word problems. And for that matter I believe that success in math & physics depends more on smartness than hard work. But I understand that other people have different beliefs in this matter. I’d rather have knowledge than belief, particularly if I have to convince people who I know believe differently.
[*] Actually, we might if we could do the apples-to-apples SAT vs GRE comparison; the women who pass the SAT gate would, in this hypothetical, improve relative to men through four years of harder work by GRE time.
Do you just mean GRE, not SAT?
GRE is a filter to enter graduate school in math or physics. But SAT is not a filter to entering undergraduate school in a particular field. Unlike in the rest of the world, Americans are admitted to college generally, not to a particular major. Large numbers of students attempt science and especially engineering, get bad grades, and switch to easier majors.
The effect is stronger at the graduate level, but it does exist at the undergraduate level. For example, at the University of Texas (my undergrad alma mater, FWIW), an engineering or natural sciences major must have a math SAT score of 600+, or ACT 26+ or one of a few other equivalents. One cannot simply “apply to UT”, and on acceptance say “OK. now I will major in engineering”.
And for that matter, if you do make it in to engineering and decide it is too hard, your subsequent transfer to art history is not automatic either, though it is likely quite a bit easier.
I think that is exceptional and virtually every other school in America works differently.
Actually, no. Engineering, specifically, tends to be an exception to “American students apply to undergraduate school generally, not to a particular field.” You usually have to apply to a specific school of engineering, with its own admissions requirements, and then once you’re accepted, you choose your major from among the subfields of engineering. This isn’t true of mathematics or “hard sciences” such as chemistry, but engineering is separate. (Music and other “fine arts” are also frequently separated into their own schools, as well.)
Are there actually people who could solve the problem above if it involves guns but not if it involves cakes, or vice versa? If so, then (a) wow, and (b) they kind of deserve to fail, because abstracting the mathematics away from the concrete example is a core mathematical skill. If you’re sufficiently distracted by girl-cootie baking or scary guns that it actually impacts your performance, then you’re already doing it wrong.
And if we weren’t doing it wrong, we would all get 800 on our math SATs. Which, possibly, all the boys and girls at Vulcan High are doing, but here on Earth one of the things we predictably do wrong is to get messy emotions mixed in with our pure reason.
Proposal for a steelmanned position: Anyone who can solve the gun one can solve the cake one and vice versa, but there are small gender-related differences in how long it takes to abstract away the irrelevant bits. This leaves less time for other problems, which affects scores on the margin.
Haishan: That, and probably a small difference in how readily a marginal test-taker will throw up his or her hands and say “This one is too hard; I’m not going to try any more”.
This should be empirically verifiable, no? Searching found Zohar and Gershikov (2007), whose full content is behind a paywall, but who have this in their abstract:
Three contexts of mathematical tasks (stereotypically boys’ contexts, stereotypically girls’ contexts and neutral contexts) are examined in three age groups (young, medium, and old). Boys’ and girls’ mean scores were compared for each age group in each of the three contexts. The data show that girls’ performance is affected by the context of the task while boys’ performance is not. The comparison between boys and girls in the three different contexts showed that in neutral contexts, the scores of boys and girls are similar. In (stereotypically) boys’ contexts, however, boys score significantly higher than girls. In (stereotypically) girls’ contexts, a significant interaction is found between age and gender, showing that the way girls are affected by such contexts depends on their age.
What’s interesting is that according to this, the finding is that stereotypically “girl” contexts also reduce female ability to correctly solve problems, with older students doing worse that younger ones. This, in turn, suggests that there is a real gender difference here, with males being better than females at decontextualizing social cues.
OTOH I found other studies which claimed the opposite, that females were better at decontextualizing, but I suspect that these studies are referring to different kinds of “decontextualization”.
Another steelmanned version: anyone who can solve one should be able to solve the other, but many people can solve one but not the other. Suppose a boy can solve the gun one but not the cake one. He should get marked down for missing the problem, but if he gets the gun version, then he will be incorrectly measured as having the proper mathematical skills. So there will be boys that should be getting a low score, that aren’t but not with girls.
Were I unaware of the differences in people’s performances on the Wason selection task depending on whether it’s expressed in terms of letters and numbers or in terms of ages and drinks, I would also strongly doubt that.
Anecdotally, for what anecdotes are worth, my recollection from (US) high school was that a lot of my male classmates vehemently hated word problems, and contrariwise the women were slightly more likely to struggle with the arithmetic itself, though not *much* more so, I think.
Also, yes, the “ew, cooties” effect is reasonably strong in men at the ages these tests are generally taken (15-18 for the SAT/ACT). I’m less sure about the effect of the reverse; I’m M2F trans so I’m far from representative, but neither “scary guns” nor “eww cooties” would have bothered me, for what little that’s worth.
Oh yeah, the word problems thing. That never made sense to me when I was in school; word problems were, mathematically, usually the easiest problems in a given set, but a lot of my classmates still seemed to struggle with them. It’s still a little remarkable to me that anyone who’s capable of understanding integrals can be that bad at reading comprehension.
I didn’t notice any gender differential, but I wasn’t exactly an acute social observer at the time. On the other hand, I remember the actual problems as generally being so contrived that any gender coding would probably have been minimal.
What does the ages-and-drinks form of the Wason selection task look like?
A while ago, there was some interesting discussion on Tumblr about the possibility that part of why people do poorly on the Wason selection task is because natural language works differently from formal logic, and the participants are mentally translating the verbal information they’re given into logic in a way that isn’t “correct” according to the definition of the task but gets more accurate results in most real-world situations.
Taymon, you’re in an establishment where alcohol is served but only to those over a certain age (let’s say, 21). You’re tasked with going around and checking to make sure alcohol isn’t being drunk by underaged people. I guess the formal rule would be “If drinking alcohol, then age >= 21.”
And people do better on this than the one with cards? Yeah, that makes sense to me, and the people who were arguing this point on Tumblr earn Bayes points.
I’m inclined to count this against the people on Tumblr.
You can read about the successful version of the Wason Selection Task wikipedia.
If it were just drinks and ages, you should be very suspicious of drawing conclusions, because that’s a specific rule that people already know, so it doesn’t tell you much about how to communicate new rules. But Cosmides claims to have synthesized lots of examples that do and do not work and to have tested her theory with new examples. She claims that it is not about word choice, not about “if…then” vs “if…must,” but about agency and especially exchange. I don’t know what “exchange” means, but agency suggests that people would pass if instead of asking about cards being correct, they were asked about people playing the cards making legal plays. But this messes with the universal quantifier. And this leaves out the part about exchange. Maybe exchange is important because it indicates that it defaults to legal: people not trying to get something are not breaking rules.
I’m coming to this conversation quite late, but it should be clear from evolutionary psychology that content can affect processing of seemingly abstract problems. This is discussed in, e.g., the Primer: http://www.cep.ucsb.edu/primer.html
Something I’ve wondered about stereotype threat– from what I’ve gathered, what’s been tested is whether people are affected by the mere reminder that they’re in a group that’s discriminated against.
Has there been any research on the effect of exposure to actual prejudice?
The stereotype threat as an explanation for the achievement gap, like most of social psychology, is wishy-washy
. http://en.wikipedia.org/wiki/Stereotype_threat#Criticism
Imagine a world where everyone within a major has the potential to score the same on the GRE. Now, in this world there is some social effect that prevents women in quantitative majors from deciding to continue on to grad work, so they never take the GRE.
In this world, the most mathematically gifted women never take the GRE, and you get a graph that looks exactly like yours.
The GRE data is also, obviously, consistent with your natural ability thesis.
The big problem here I think is that all the differences either model predicts aren’t in the set of test takers, they are in the set of people who don’t take the test, which you have no data on.
“In this world, the most mathematically gifted women never take the GRE, and you get a graph that looks exactly like yours.”
Scott addressed this point through the SAT scores. The SAT math distributions of the two sexes stay almost the same in the GRE. If the most mathematically gifted female students are choosing not to apply to graduate programs in mathematics, you would expect that the math percentile scores for women be lower on the GRE than in the SAT.
The post explicitly raises this question and uses SATs to test it.
Why would these social effects disproportionately affect the most gifted women?
Absent such a disproportionate effect, all this effect would do us reduce the # of women taking the GRE – the distribution of ability among the women who take it would remain the same.
Question about stereotype threat. I am not a social scientist and not very well read in this field, so I could be misunderstanding things. But my understanding was that stereotype threat studies were using short term laboratory tests to try to probe at effects of life-long socialization – the idea being that while your specific laboratory manipulation has increased the gender gap in test scores by some small percent, it is demonstrating a plausible way in which real-life social factors could cause a larger test score gap over the course of decades.
Obviously, it’s a non-trivial assumption that a small laboratory effects are indicative of a larger, additive real-world effect. But if true, it could plausibly explain test score gaps, no? That’s the argument I would expect people to make, anyway.
This was my understanding as well.
One would have to not only posit that such an effect exist, but that that effect somehow applies only to tests and not to “real” work. If women don’t solve mathematical problems as well as men because of socialization, that still means that women don’t solve mathematical problems as well as men. It doesn’t do anything to support the idea that it’s the fields that are discriminatory.
IIRC there was a post about that on this blog, but I can’t remember its title.
Scott wrote about stereotype threat in “Social Psychology Is a Flamethrower” and also touched on it in “Genetic Testing and Self-Fulfilling Prophecies”.
There’s an argument that I rarely see addressed in these discussions. It’s one I personally hold to, and I think a lot of other social leftists also hold it implicitly or explicitly, but by its nature it never gets voiced. But here it is:
I don’t care whether or not, empirically, there are gender (or racial) differences in raw performance, because I think it is a bit of knowledge that has, on a societal level, only a little positive use and very substantial downsides/danger.
I doubt anyone here would dispute that human beings are not good at understanding or dealing with statistics or distribution curves. An educated person who has thought at length about the issue can internalize the idea that the fairly subtle statistical trends discussed in this article can explain certain social phenomena while also understanding that it gives them little-to-no information about any particular individual they might happen to meet. But that’s a difficult and uphill battle–it requires avoiding both the Fundamental Attribution Error and a set of historical stereotypes that have had centuries to accrete. Frankly, it is a battle most people are going to lose–and that’s assuming a good faith effort. In reality, history strongly indicates that there are a great many people who will instead exploit those stereotypes for their own purposes.
And what does it give us? Well, the truth. I do consider that an important end in itself–but I don’t consider it dispositive, and I sincerely hope that anyone who does has at least sat down and acknowledged that the position of “truth above all” is no less an aesthetic/ideological position than “equality above all.” Other than that? It is more fair to the white-male-types on the margins who would lose out to affirmative actions taken on the basis of inaccurate data and assumptions, which is also a good end in itself but also seems to me to not be dispositive. And, theoretically, it could save us from wasting resources trying to correct supposed causal factors that are not, in fact, causal–but at least from where I sit, we’re still in debt to history, and need to make much more recompensation before we could possibly classify it as waste (I acknowledge that a lot of people disagree with me on this one).
All in all, these moderate positives just aren’t good enough for me. A world where everyone knows that certain groups are empirically less able in certain areas is one with a very, very high risk of going back to the bad old days, where women and minorities with substantial and genuine talent nonetheless face an unfair, uphill battle for success and recognition. The world where we instead pretend and assume that these classes are all equal seems to me to be a far better place to live, even as a white male who has always done well on standardized tests and other measures of raw intelligence.
At any rate, I could be wrong, but I do wish the possibility that the truth isn’t an unmitigated good had a little more play in places like this.
Do you know of research on whether people tend to overestimate the effects of real differences?
I know the Fundemental Attribution Bias, wherein people leap to explanations based on intrinsic traits rather than particular circumstances to explain behavior of others (but not self), has been studied at length; overestimating the importance of intrinsic traits seems to me a pretty logical extrapolation of that… but I don’t have anything on hand nor any kind of journal access (my field is law, which probably acts as an ironic “what do you call a thousand lawyers at the bottom of the ocean”-type commentary on my interest in the positive vs. negative use-value of a given bit of knowledge).
Lee Jussim:
http://www.rci.rutgers.edu/~jussim/unbearable%20accuracy%20of%20stereotypes.pdf
This paper is about people attributing invented differences to gender, which probably goes to the same points.
This paper, that is. I was posting from a new tablet!
https://psych.princeton.edu/psychology/research/prentice/pubs/essentialism.pdf
I recommend reading it. It’s sort of subtly hilarious. People infer gender stereotypes on completely invented cognitive attributes from a sample of n=1.
Furthermore, if they decide based on their generalisation from a sample of n=1 that their failure mode on (completely invented cognitive attribute) is due to the gender stereotype they just made up in their heads, they don’t try to correct the failure.
I adore it.
I don’t know, I feel like part of the reason people thought there would be group differences is because the questionnaire prepared by psychology researchers included questions about group differences. It would be a logical inference to expect differences, if that is what you think the researchers are studying.
It would be fun if they had actually scored people as overestimators or underestimators, and seen if there opinions were actually accurate or not. It could be that the people were actually accurate based on the structure of the test combined with other knowledge, but the researchers have no way of knowing because of how it was designed.
No, it makes sense to assume group differences iff assuming group differences is something you’re already inclined to do. Which is the point they’re making there. If it seems somehow obvious to you that people might make that assumption in those circumstances, that only strengthens the point!
I can’t work out exactly what you mean in your second point. I don’t see how genuinely scoring people could possibly have been interesting or useful.
Maybe you’re saying that people didn’t correct for “overestimation” or “underestimation” because they knew they had been accurate? But then why did they correct in the same-sex condition?
Or are you suggesting that there might be an actual effect of gender on “dot estimation?” Even if there was (lol!l) what they’re showing there is that people concoct stereotypes based on randomly assigned scores. Knowing their actual scores has no relevance to that result.
“No, it makes sense to assume group differences iff assuming group differences is something you’re already inclined to do.”
“Inclined to do” is a pretty wishy-washy statement here. Obviously you won’t hypothesize group differences unless you are in some sense predisposed to discovering them even if they are valid. My supposition is that people won’t have considered that there is a gender difference in test scores in absence of being asked about the gender difference in test scores. Being asked about the gender difference of test scores when you are an undergraduate enrolled in psychology courses and taking a study for credit / extra credit is weak evidence (but still evidence!) that you should expect a gender difference in your score.
On my second point, I am indeed suggesting that there may be a gender effect on dot estimation, which you are lol!ling about. Without seeing the data, I am apparently far less confident than you that there is absolutely no gender dependence on the first attempt at this task. I understand that this wouldn’t help the researchers find what they are looking for, which is why I described it as “fun” rather than “necessary for intellectual honesty.” The difference in people’s behaviors in the mixed case vs. the same case is indeed the most interesting part of the study, however, as you are implicitly suggesting.
The problem with saying that people concoct stories based on randomly assigned scores is that the people in the study have no way of knowing that the scores are randomly asssigned. Given that there are so many aspects of personality and behavior that are studied which do indeed have correlations with gender when they are not randomly assigned, assuming that this particular case is an exception would be the more unlikely situation, in my opinion. You can’t just pretend people don’t know things like this if you want to have actually applicable studies. This is exactly the source of the replication problem.
You can’t interpret the first experiment on its own though. It’s there because it’s a necessary precursor for the second experiment.
Note that in the second experiment, no one asked the question about gender. But there’s still evidence that the gender stereotyping is happening. So your assumption that the stereotyping wouldn’t have happened if people weren’t asked about it doesn’t stand up to the evidence here.
Also, the reason I found the interest in actual gender differences in “dot estimation” amusing is not because I am “confident there is absolutely no gender dependence on the first attempt at this task.” It’s for much the same reason I find the original paper amusing. But it was a bit obnoxious of me to put in the lol. Sorry about that.
> it makes sense to assume group differences iff assuming group differences is something you’re already inclined to do.
One of my physics professors said, “Every effect not forbidden by symmetry exists.” (exact quote). Then he went on to say that not every effect is significant.
So yeah, there’s guaranteed to be a difference because we are way way far away from fundamental symmetries here. But it can very easily be an insignificant difference by any vaguely reasonable standard of significance.
This is a pretty important claim, and I hope this gets addressed here or somewhere else. It seems that the tide is shifting in favor of Charles Murray’s position — that gender/racial differences in achievement are best explained by the IQ distribution bell curve. Perhaps our institutions only work so well because people assume that there are no innate gender/race differences. If the knowledge that a lot of differences in achievement can be explained through nature becomes widely acknowledged, I would expect to see more discrimination especially when subjective evaluations are involved. This could ultimately throw off the predictive power of the IQ curve.
What leads to your belief that the tide is shifting? Alternative hypothesis: your environment has shifted because you have changed environments.
Careful. Differences in IQ scores don’t automatically imply “innate” differences. There is, in fact, good reason to believe that we can remedy some gaps by actually increasing IQ.
For example, IQ scores of USA blacks have gone up substantially in the last 40 years. (Black poverty has also gone way down over that time, which I daresay is probably the cause.) There are other examples where IQ scores differ between populations that ought to have more or less identical genetics.
Furthermore, even “innate” in the sense of (say) genetic does not imply something that cannot be changed! We are on the verge of rewriting our own genome and we are certainly going to be finding and widely-propagating genes that enhance human intelligence.
US Black IQ scores have gone up by maybe 3 points in the past 40 years.
About twice that.
http://www.brookings.edu/research/articles/2006/10/affirmativeaction-dickens
“We analyze data from nine standardization samples for four major tests of cognitive ability. These suggest that blacks have gained 5 or 6 IQ points on non-Hispanic whites between 1972 and 2002. ”
(Note that white IQs also went up during that time.)
I got the number 3 from figure 2 of that paper on page 29. If the authors disagree, so much the worse for them.
How did you get the number 3 from that figure? It’s a line graph showing scores on various tests at various times.
The text from the paper that describes those scores and shows how they derived a total figure:
Differences between black IQs from one standardization to another give estimates
of the rate of gain. The WAIS (under 25) shows 3.22 points gained over 17 years (rate =
0.189 points per year). The AFQT shows 3.62 points over 17 years (rate = 0.213). The
SB shows 1.79 points over 16 years (rate = 0.112). The WISC shows 1.51 points from
1972 to 1989 (rate = .089) and 4.16 points from 1989 to 2002 (rate = 0.320). Averaging
these gives a rate of gain of 0.185 points per year
(Note 0.185*40 = 7.4)
Of course, one could argue that simply averaging the score changes from these different tests is overly simple. There are certainly large discrepancies between the tests. But I’m curious how you derived 3?
hmm..if SAT/ACT or AFQT scores are a proxy for IQ, blacks are much lower than whites; this suggets a fairly substantial IQ difference http://3.bp.blogspot.com/-Myld998sNf0/UmjCOUAXHkI/AAAAAAAAA6w/vTAKdL__uLk/s1600/sat-act+race.png
a meta analysis shows a persistent .5-1 SD difference between blacks and whites http://www.brookings.edu/views/papers/dickens/20060619_IQ.pdf
First of all, no, SAT/ACT scores are not a proxy for IQ over time, even if we assume SAT scores are a proxy for IQ, because of self-selection (you’ll be measuring changes in how many people from groups have taken the test).
Second, you seem not to be addressing the point I made.
Aside commitment to truth in the abstract, false beliefs also have the problem of people actually acting as though their beliefs are true.
The belief you describe might not be so bad by itself (though of course there is the question of whether social tolerance of any falsity isn’t going to suffer a generalized degeneration of its pursuit of truth), but where does it tell you to go? Because if there are differences, and everybody treats everybody the same, then the outcomes are going to be different, and that is going to show up in the statistics, and if you believe that there are no innate differences, this is a sign of a serious problem. As, indeed, we see. And then people will propose radical changes to solve that problem, and even if they’re implemented it won’t change anything, and there will be all this damage to various fields being undertaken in the name of treatment for a disease that nobody has.
“Wasting resources” is a bit of a mild way to put it. We’ve got people trying to completely change the culture of productive communities for the sake of addressing these problems, which may not even exist at the level they’re attacking.
But now, going back to the point put aside earlier, you can’t just pick and choose where we pursue the truth. Favoring deliberate misinformation in this case is to also throw your support to every other effort like it, and there is no cause whose true believers do not consider it worth lying for. Is it really possible to have the sort of mindset that pursues truth, except when it’s politically inconvenient? Of course it is. That’s everybody in all eras by default. Discarding the commitment to total truth in any area is the equivalent of discarding the entire virtue of truth itself, because it’s only when it’s the right choice is difficult are virtues needed at all.
“we’re still in debt to history, and need to make much more recompensation before we could possibly classify it as waste”
What does this mean? We can’t “pay back” injustices against previous generations of women by inflicting injustices on the current generation of men. You can’t restore lost utility in the past by decreasing present utility.
If you mean “past prejudice still has persistent impact in the present”, well, that’s exactly what Scott’s analysis is meant to address, isn’t it? Assuming his conclusion for the moment, if it’s true that gender representation closely tracks innate ability, then I don’t see where there are relevant impacts to fix. If Scott is wrong, then prove it. If there are consequences to admitting that Scott is right, prove those. Your hypothesis is interesting, but you need a better argument then “I’m scared of the impact of admitting the truth”. Hopefully you can understand why that’s a tough argument to pose to a forum of self styled rationalists?
This is a consistent problem I have with “gender under representation” research: illogically defined goalposts. To me, the “perfectly equal” world is one in which everyone who wants to do something can do it, not necessarily the one in which representation in every field perfectly matches the global demographics. And anyway, if the latter is what you really want, you’re going to need to start addressing the male underrepresentation in higher ed in general, and many fields in particular, pretty soon.
Finally, there’s a couple strong negatives of “hide the truth” you ignore: women who are discouraged from going into a field because well meaning feminist groups do more damage through stereotype threat than actual discrimination does, and women who don’t really want to (or lack the innate ability to) go into STEM fields but are nudged into doing so to boost the bottom line gender percentage.
Anecdotally, I knew a few cases of the latter in college – women who went to engineering college because they were offered lucrative women’s only scholarships, but quickly dropped out because they were never that interested and found they were miserable. That seems to be a pretty obvious utility loss – women made miserable, and a reduced number of actually interested engineering graduates able to help the world.
But the trouble is that such things as sexism and racism do exist.
African-American Joe at age twelve is subtly and not so subtly discouraged from taking higher level maths classes by his teachers because “Science has proved African-Americans are less innately able to do mathematics, here are the impartial studies, why don’t you put that effort into something you would be good at, Joe?”
Same for twelve year old Sally.
Twelve year old African-American Katie has the worst of it, getting the double-whammy of belonging to two groups which have been demonstrated to lack the ability for the field required.
And don’t say “Oh, but if Joe and Sally and Katie are good at maths, that won’t matter what their teachers and careers advisors say!” Because it does matter (for instance, I wanted to do Latin when I started secondary school but the teacher refused to take me. Would I have been any good? No idea, but I never got the chance to try. I did German, dropped it after a year because I wasn’t much good at it and hated the language and stuck with French instead).
Objective truth on non-biased tests is one thing. But the way the results of those tests will be used by both sides of the debate is not as clear-cut. You’ll have those eager to say “See, we told you there was no discrimination against women/blacks/Jews! They just don’t have the ability needed! It’s not their fault they’re less intelligent, of course, nobody is blaming them, but facts are facts.”
what is your evidence that teachers discourage blacks and women these days from science and math? any studies to support that claim?
isn’t it just the reverse – there are special efforts to help them? black kids are disadvantaged in math because they are locked in crummy public schools with chaotic classrooms. Evidence: charter schools in New York raised performance on math tests by an average of two grades among the highest at risk previously failing black students.
the other disastrous factor in blacks going into science and math is peer pressure to reject education as too white, aided by all the money to be made by makes gangsta’s heros in the music industry. there are NO teachers who agree with that.
Racism and sexism do exist, but that doesn’t mean you get to assume their impact without evidence. And the fact that some people might abuse the evidence isn’t an argument against the evidence.
Actually it’s worse than that, because you seem to be saying “the fact that racism and sexism could conceivably have an impact on this result means that any research into factors other than racism and sexism is prima facie false and dangerous”.
What I really need to see evidence of is that there are women who really want to do STEM, and are really good at STEM, but can’t due to discrimination. One potential idea would be to compare the scores of people who start STEM but drop out of the field – if the women who drop out have higher scores, that might suggest something other than innate ability is at work.
Anyway, I’m curious what your thoughts are on the negatives I brought up – what of the women shepherded into STEM who aren’t naturally interested in order to “cast a wider net” to use a phrase of yours? That seems bad.
Perhaps a factor (with a statistic to match) which influences US women’s choices to drop out, is what Larry Summers called
“the high-powered job hypothesis.”
Speaking of the upper, most prestigious, highest paid, ranks (“chief executive officers at major corporations, the managing partners of large law firms, the directors of prominent teaching hospitals, and with the leaders of other prominent professional service organizations, as well as with colleagues in higher education”) he says:
[T]he most prestigious activities in our society expect of people who are going to rise to leadership positions in their forties near total commitments to their work. They expect a large number of hours in the office, they expect a flexibility of schedules to respond to contingency, they expect a continuity of effort through the life cycle, and they expect-and this is harder to measure-but they expect that the mind is always working on the problems that are in the job, even when the job is not taking place.
Another way to put the point is to say, what fraction of young women in their mid-twenties make a decision that they don’t want to have a job that they think about eighty hours a week.
[….] [T]he relatively few women who are in the highest ranking places are disproportionately either unmarried or without children [….]
http://www.harvard.edu/president/speeches/summers_2005/nber.php
“You can’t restore lost utility in the past by decreasing present utility.”
Actually, I think in some cases you can. Suppose your best friend dies, and their dying wish is to be buried at sea. You don’t think there is anything particularly good about being buried in the sea–dead is dead–but it’s what they wanted, so shouldn’t you do it? Even if you never explicitly promised them you would because they died before you had a chance to respond?
Because if history teaches us anything, it’s that whenever a society stops caring about truth it’s always the noble lies that win out.
But that noble lie was probably crafted by those very same people with “high IQ” and “innate intelligence”. This is an outrage!
The paper I linked above discusses this a little. Stereotypes become a self-fulfilling prophecy through mechanisms much less crude than “stereotype threat.”
I think it’s really important to note that other mechanisms than stereotype threat and innate ability do exist to explain these results. Which is why I’m pasting the link again!
http://web.stanford.edu/dept/psychology/cgi-bin/drupalm/system/files/cdweckmathgift.pdf
But yeah, supposing innate differences to exist, constant discussion and reinforcement of them would massively magnify their impact.
We wouldn’t need to constantly discus them if nobody constantly called attention to the statistical disparity as evidence of society’s moral failure.
That paper provides a superficially plausible mechanism for the results we see among the few percent of the population who go on to graduate study in certain fields, but it does nothing to explain the data underlying the “innate ability” thesis.
Do you mean the differences in IQ distributions or something else?
What data are you referring to?
I think this mechanism explains a lot more than just the results among the few percent of the population who go on to graduate study. You saw the study was was conducted on fifth graders.
I have spent a lot of time thinking about this point, but have come to the exact opposite conclusion.
This is actually a really important point, first on an ‘effectively resolving this problem’ count, on the ‘why does it matter’ count, and on the ‘why do we care’ count
Resolving the problem:
Let us assume for the moment that women are under-represented in STEM (relative to where they ‘should’ be), but we do not know the reason why. If the reason why comes from some combination of history, prejudice, oppression, stereotype threat, etc., then the most effective solution to stop the under-representation is a sort of affirmative action policy. This is illustrated nicely here.
If, on the other hand, the reason is primarily innate ability, combined with perhaps some sloppy thinking (so, essentially, innate ability + some people use innate ability to inform stereotypes which gives “women and minorities with substantial and genuine talent nonetheless face an unfair, uphill battle for success and recognition”), then this is important to know. Because in this world, we want to prevent the bias against people of genuine talent, but said bias is *not* caused by historical effects. In this world, affirmative action wouldn’t be necessary. All we would need is to eliminate opportunity for stereotyping. Using gender-blind hiring and interview practices, for example. Basing more things on impartial tests and fewer things on human judgement, etc.
Why does it matter:
Step back for a second and think: why does a gender gap in STEM matter? The easy answer is, again, “women and minorities with substantial and genuine talent nonetheless face an unfair, uphill battle for success and recognition”, but in a world where people are judged solely on ability, that doesn’t happen. I think there is a potential disagreement of norms here between people who talk about this, so I’ll state it plainly: in a world where the gender gap is informed by innate differences, I believe the gender gap is fair, just, and *not a problem*. Full stop. I suspect many people disagree with this, and believe that there is something intrinsically desirable to a gender balance in a given area, regardless.
However, here’s the problem. Hypothesize that the software engineering (to use an example I’m familiar with) gender gap is completely informed by intrinsic ability, and its current position (~15% female by my estimate, or 3/20) is its natural resting place. In this world, artificially changing the balance to be equal means intentionally removing 7 able (male) developers and replacing them with 7 less able female developers. IN A WORLD where the gender gap is informed by social influences, this is a good thing. In a world where this is informed by intrinsic ability, this makes all of society worse off (on comparative-advantage grounds).
In addition to this, there’s the personal welfare aspect. Scott touched on this in the draft of this post but removed it from the published version. If the difference is all in innate ability, then shoehorning people into positions they aren’t cut out for is a bad idea. On the best case, you’re slotting people into jobs they don’t like. On the worst case, you’re streaming people to waste tons of time and money on a college degree in a field in which they’re unemployable because they don’t have the intrinsic ability. These are all bad.
Why do we care?
This is a question I’d actually really like answered, but it’s one that just can’t be answered in public. Why do we actually care about a gender gap in STEM. We don’t care about the gender gap in female-dominated majors. What is the difference? Everyone involved in these discussions seems to just take for granted that this is a thing that is important, but nobody ever answers why.
My hunch, is that most of the fields with a big gender imbalance in favour of men are high prestige and high pay. Most of the fields with a big gender imbalance in favour of women are not. Regardless of any other disparities, most of us agree that men and women should be on equal economic and social footing. And so when people see a gender gap in STEM, they conflate the job with the economic and social status.
If this is true, then this gives us a really really really easy way out of this discussion. If the *reason we care* about gender gaps in STEM is because of the associated economic inequality that results, we have the option of addressing the economic inequality directly, without having to proxy it through a certain set of fields. If we could do that, then this entire conversation actually becomes moot, without risking any negativity on any end.
—-
In short: knowing peoples strengths and weaknesses is intrinsically important, because the most optimal world is the world where everyone is doing the thing they’re best at. If there is a statistically significant difference in innate ability informing gender gaps in STEM fields, then per the last sentence, those gaps are justified and acceptable. This is not to say that it is acceptable to stereotype people based on their genders (human variance is very high; the fact that women as a whole may score lower on math ability tells you very little about any individual woman), but simply to inform us on where to calibrate our expectations re: gender gap. If the gender gap is mostly socially constructed, anything that isn’t parity is probably wrong. If the gender gap is primarily reflective of ability, then in and of itself it is not a bad thing. Finally: what actual, specific reasons do we care about a gender gap. Is it possible to address those reasons directly without proxying through intrinsic ability discussion at all? If so, we should do that
>Let us assume for the moment that women are under-represented in STEM (relative to where they ‘should’ be), but we do not know the reason why. If the reason why comes from some combination of history, prejudice, oppression, stereotype threat, etc., then the most effective solution to stop the under-representation is a sort of affirmative action policy. This is illustrated nicely here.
The cute little triangles and squares in that app conveniently fails to mention the very ugly and very sensible reasons why different races don’t like living around each other.
Also, as was pointed out by another commenter when this was first linked here, if you set the ratio to be comparable to the white/black ratio in American, then segregation is driven almost entirely by the minority having to cluster together in order to live next to others of their kind.
Indeed, the model is limited because it doesn’t factor in how well “niceness of neighborhood” (or “murder rate”) correlates to triangle-ness or square-ness. To that extent, White Flight isn’t represented accurately.
In any event, terrifying things start to happen when you reduce the amount of free space (i.e. once you run out of land to build exurbs for white people to flee into).
Also I think it’s funny how even if you set their diversity preference to zero, none of the shapes ever rise above neutral faces. They’re hardcoded to be only happy if they have diversity. It’s the little things …
I’ve also been thinking about this for a long time, and I’ve come to a similar conclusion. Assuming that it is indeed true, I also think it’s a supreme irony: certain feminists have been pointing out for decades that society undervalues the types of work typically done by women (which I think is absolutely true). Meanwhile, other feminists are trying to solve a related problem in precisely the wrong way: by pushing women away from economically unrewarding careers that they might nevertheless enjoy more, and in effect perpetuating the undervaluing of those types of careers.
They’re trying to solve a related, but different problem. I’m not arguing in favour of their solution, but calling it “wrong” for its effect on a different thing is just weird.
You’re right, this sentence was poorly worded. The main point I was trying to make was that attempts to solve the latter “problem” might actually exacerbate the former problem, which is a bigger problem (IMO). But indeed, I phrased it quite poorly.
“Society values”? It’s not like wages for the type of work typically done by females were deliberately set lower in some kind of government meeting! There is some demand for that kind of work, and there is some supply for it, and the point at which these quantities meet is the salary the market pays for such work. Is the fix supposed to be some kind of redistribution scheme?
I think Platypus is referring to the Marxist-feminist concepts of “affective labor” and similar that underlay the wages-for-housework movement. The idea, so far as I understand it, was that bourgeois ideology requires women to do certain forms of work (e.g. childcare or housecleaning) without monetary compensation out of “love for family,” and that such concepts as “love for family” are fig leaves for removing women’s autonomy (financial and, as a consequence, otherwise). One of our resident Marxists could explain it better than I could.
I often come across the notion, from economics types, that the only value worth considering is market value. Yet, here is an example of someone talking about the very thing and someone chimes in to complain that it’s a redistributionist plot. I just really don’t understand economics, I guess.
@jaimeastorga200: Yes, “society does x” is an extremely broad abstraction, but that doesn’t mean it can’t be true. I think viewing this only as a question of supply and demand as scalar quantities is overly reductive given that we are discussing about the social and/or innate factors which determine the supply of workers for different professions (and probably also the demand for those workers, to an extent). Most people don’t choose their major in college by looking at a supply vs. demand graph and trying to find the most lucrative career that they think they’re capable of achieving.
More importantly, demand is not just a question of how many warm bodies we need to do some task, but also how skilled we expect those individuals to be at that task. We have very high standards for some jobs and quite low standards for others; when I say that we undervalue “women’s work,” I mainly mean that we have low standards for jobs which are actually quite important, and this leads to the supply of workers exceeding the demand and compensation for the profession going down.
For example, teaching is a female-dominated profession. Purely in terms of numbers, the demand for teachers is probably some relatively fixed percentage of the general population. But in terms of aptitude, we have relatively low expectations for individuals who pursue this career [citation needed]. This leads to supply exceeding demand and relatively low wages. We do get some very good teachers, but we also get a lot of shit teachers. If we could set the bar higher for teachers, supply would no longer outstrip demand to such an extent, so wages would go up, and we’d attract more talented individuals who might have gone into the field if not for its low pay grade, thereby still satisfying the demanded quantity of teachers. Since the profession is female-dominated, this would lead to higher average pay for women, but more importantly, it might also increase the quality of education that kids receive. I think that last bit is very important, even though I personally don’t plan to have kids.
(In response to Wulfrickson, careers like teaching are actually what I’m talking about; I’m aware of the theory you mentioned but it seems absurd on to me for a variety of reasons. I guess it could be part of some solution to this problem, but not one that I can envision actually working.)
I am well aware that this requires a massive amount of change and is an exceedingly difficult problem to solve. However, I’m not convinced that it’s more difficult than radically changing STEM culture/getting rid of gendered socialization/any of the solutions third-wave (Internet?) feminists seem to be proposing. Additionally, I am not proposing a particular solution—I don’t think I’m nearly smart or knowledgeable enough to do so. I’m just saying that I think a solution based on these observations, if one could be implemented, might actually work, whereas I don’t believe that “solutions” like subjecting tech workers to diversity seminars will do jack shit, for reasons Scott has discussed at length in this post and others.
““Society values”? It’s not like wages for the type of work typically done by females were deliberately set lower in some kind of government meeting!”
In your worldview, is government the only means through which society’s values is expressed?
^ I endorse Platypus’ explaination
If the *reason we care* about gender gaps in STEM is because of the associated economic inequality that results, we have the option of addressing the economic inequality directly, without having to proxy it through a certain set of fields.
But when we consider where the money is coming from, the direct method looks less feasible. Much of STEM money comes from the federal government through Congress, and much from customers. Letting more women into the higher paying fields, is really easier than trying to persuade Congress to support more soft sciences grants — or to persuade tech customers to spend their money elsewhere.
Note that I said “letting”, not “shoehorning” or “slotting” or nudging any girl into studies she’s not interested in. Rather, removing obstacles for the girls and women who actually have STEM interests.
As for the welfare of the fields, if women are so different from men, then they may bring new ways to get better results.
Letting vs. nudging/shoehorning relies on there actually being obstacles to remove, and that’s what this whole discussion is about. No fair begging the question.
Personally, I think that if there are structural obstacles/biases keeping women out of STEM, they are acting a lot earlier than colleges and professionals (and yet that’s where all the effort is being focused). By the time you get to college prep, the pro-women-in-STEM message is already pervasive, the support widely advertised, the hiring affirmative action accepted as a given (I base this on recently going through the engineering college at a large public university and working for a medium-large defense contractor). I have personally witnessed women being “nudged” to the point that they rapidly realized they were actually miserable and dropped out.
I suspect that the vast majority of women who really want to do STEM by the time they get to college are already doing it (so much so that a lot of women receiving the gender specific help in college don’t really need it – they would do fine on their own). If you want more women in the field you need to start hitting it at the elementary and middle school level.
The only real barriers I’ve personally witnessed are 1) dirty old men in the field (most of whom will leave the workforce soon anyway) and 2) general discomfort with being one of only a few women in the office. 2) is not trivial, but it’s also debatable whether fixing that is a good idea once the field hits it’s “natural” gender distribution.
I’ve played with the square-triangle thingy a while back, but I don’t see how it makes a case for affirmative action. Can you elaborate?
“If the reason why comes from some combination of history, prejudice, oppression, stereotype threat, etc., then the most effective solution to stop the under-representation is a sort of affirmative action policy.”
I don’t see how.
I just want to thank nil for making this post. I disagree with it—I think, on consequentialist rather than ideological grounds, that a very strong bias in favor of truth is desirable. But it is an argument worth making and considering, and it’s one that you surely knew would be unpopular in this forum.
As I like to put it, “some statements are both true and dangerous, and this is one such.”
“I don’t care whether or not, empirically, there are gender (or racial) differences in raw performance, because I think it is a bit of knowledge that has, on a societal level, only a little positive use and very substantial downsides/danger.”
This is an important point and I’m glad you brought it up. I don’t necessarily reject it in all cases, but in this case I think it’s worth bringing up for a few reasons.
First of all, if gender differences in ability are true, the failure of (most) science to notice they’re true, and the overwhelming success of science in “proving” again and again that they’re not true, is really scary. It means that science can be really really easily corrupted for political ends and that we don’t actually know very much about society or psychology at all. Even if there’s no reason to care about the truth regarding gender+ability, probably some of the other science that we’re getting really wrong answers on does matter, a lot. The paper mentioned in this post was published in Science. If my criticism is accurate, it means we can’t necessarily trust results in Science to be better than “a random blogger can debunk them in two days with SPSS”, and that leaves us in a really bad place. This is sufficiently terrifying that it probably needs to be dragged out into the open kicking and screaming.
Second of all, if we’re misidentifying the problem we can’t solve it. Everyone assumes I’m talking about innate biological differences, and I certainly have some sympathy for that view, but I honestly haven’t ruled out differences in socialization starting as early as elementary school. If that’s true, then all of this talk of sexism in math departments is a giant distraction that’s not helping women and which is giving cover to the real problem. And because of (1), the scientific community has necessarily abdicated its responsibility to help us figure out where the real problem is. This is kind of related to one of this blog’s unofficial mottos, which is “tell one lie and the truth is forever after your enemy”.
Third of all, people won’t leave well enough alone. People are using this as a club to beat up nerds with (see Untitled), and everybody who’s convinced that sexism in Silicon Valley is what’s keeping women out of computer science is that much more aid and comfort for Shanley-style people. This offends my personal sensibilities, but more important I think Silicon Valley has the potential to be a huge force for good, and this is exactly the issue that people who don’t like good are going to use to stop it. As long as It Is Known that people in tech are bros and sexists, we can regulate the hell out of Uber and Lyft and AirBnB and drones and self-driving cars and whatever the heck else we want to regulate the hell out, because the people involved are Bad People who are probably using their fortunes to Fight Progress. I would be delighted with an armed truce between tech nerds and diversity warriors, but a “they get to bash you as much as you want, and you may never respond for the sake of preserving people’s self-esteem” rule isn’t going to fly. This is one reason I don’t talk about this except when they start it – I want to make it clear that I’m not pushing this issue, but I’m also not going to let other people get away with stuff.
Fourth of all and by far most important, the reason this result in particular has made me speak out is that a lot of the coverage focuses upon “destroying the myth of genius” and stuff of that ilk. I find “we don’t like the implications of ability, therefore let’s deny that ability exists at all” really really dystopian, and although it’s not doing dystopian stuff now, I feel like by the time it’s actually doing dystopian stuff it will probably be too late to stop it. I continue to think that the field of intelligence studies is the most important field in all of science, that it’s vitally important for the human race, and that if we devoted the same level of resources and attention to actually raising human ability as we do to screaming about sexism in tech, we would have solved most of the world’s problems by now. In particular, I am becoming more and more convinced that the route to a positive Singularity goes through human intelligence enhancement. Stick a couple of thousand von Neumann level supergeniuses on the problem – a program which would take only a decade or two to start with our current level of knowledge if there were political will – and we’d have a much better chance than anything we’re doing right now. Even if the Singularity turns out to be a false alarm, I can still think of things we’d want a thousand von Neumanns to solve (fusion power, malaria, desalinization for water-poor areas, safe geoengineering that prevents global warming). And I can’t think of an issue that wouldn’t benefit immensely from raising average IQ ten points (for example, we essentially solved crime by accident by raising IQ a little bit – see the work on lead). Neglecting intelligence might be literally the biggest mistake the human species has ever made, and instead we’re stuck arguing against people trying to “destroy” the “myth” that intelligence exists or matters. I am despairing of ever being able to do the thing we have to do to solve our currently intractable problems without first bulldozing the structure that profits from keeping people convinced that intelligence doesn’t exist.
So basically – if someone from the Secret Conspiracy Of People Who Agree Not To Talk About This approaches me, I’m on board if and only if they’re committed to good science otherwise, if they can use their Illuminati powers to agree not to use this as a club to beat science nerds with, and if they don’t throw the field of intelligence studies under the bus in order to maintain the masquerade.
“we don’t like the implications of ability, therefore let’s deny that ability exists at all”
That is not my understanding of “destroying the myth of genius.” My understanding is that people who use phrases are talking about emphasising the perspiration part over the inspiration part. And in particular they’re talking about the idea that it’s actually intelligence-destroying to assume that ability is innate.
This piece of research seems to be exactly along those lines, though I agree with you that it doesn’t prove what it set out to prove.
In general it seems to me that the researchers who want to “destroy the myth of genius” are doing work in describing how people become intelligent.
Even if you’re right, I continue to think that we need huge emphasis on the innate portion of ability in order to encourage people to figure out how to increase it.
Hard work may count for something, but the village idiot is never going to become Johann von Neumann (who could already divide 8 digit numbers in his head at age 6, apparently without any deliberate effort to learn the ability) and we NEED von Neumann.
Okay, fine, this is going to turn into another blog post, we’ll continue this discussion after it happens.
Has anyone thought of starting off just by cloning Von Neumann? I’m sure we could find his DNA. Once we clone some gametes, we can start mass-producing sperm. Then we just nationalize all sperm banks and we’re well on our way.
Has anyone thought of starting off just by cloning Von Neumann?
Approaching from kinda the same direction but not so far out, what about finding some people who are very productive and considered genius level, and studying them. I’d start with asking them what influences had helped or hindered their development and their recognition. Also find out their test scores all the way back, look at their biological background, etc. And maybe put the whole problem to them, and consider taking their advice.
“Johann von Neumann (who could already divide 8 digit numbers in his head at age 6, apparently without any deliberate effort to learn the ability)”
Do you have a convincing source for this claim?
I do not believe that anyone in history has been convincingly documented as being able to do complex mathematics without large amounts of practice. I have seen many similar claims, none of which stand up to critical scrutiny.
I think this is a classic example of the kind of far-fetched, unsubstantiated stories that lead to there being a “myth of genius”.
It can hardly be a coincidence that literally 100% of our greatest scientists have been human. Clearly, genetics play some factor.
That’s only partly a joke: if intelligence was not both genetic and variable within the population, it could not have been acted on by natural selection to get us where we are.
” It means that science can be really really easily corrupted for political ends and that we don’t actually know very much about society or psychology at all”
Isn’t this obvious?
The Dodo bird verdict is a serious contender in explaining psychology (not saying its true but it being serious is damning to the field). There is really no consensus on fundamental issues in economics. For example it is not really possible to determine with high accuracy whether Scott Sumner or X-mainstream economist has the right general idea. Do I actually need an example to show most problems in sociology are unanswered.
This isn’t to say we know nothing. There is alot of useful knowledge about what psychiatric drugs. And some solid things have been learned in psychology and economics. But we are really far from understanding psychology or society. I thought this was pretty clear.
Also it should be even more obvious that if a subject is politicized you cannot trust any journal. Notably you also usually cannot trust the “anti-mainstream” as frequently they are very ideological too.
Really the only silver lining is that scientists rarely fabricate date. They often twist the data or p-hack or write totally unsupported conclusions. But outright fraud is rare. So there is hope, the rot only goes so deep.
Who needs to fabricate data when you can fabricate definitions? eg, this paper defines the GRE score to be the math score plus twice the verbal score, plus some writing.
I agree that one doesn’t need to fabricate data. Examples abound of people coming to absurd conclusions in published important papers. via things like cleverly chosen definitions.
But as long as the data itself isn’t corrupted its still possible to make some sense out of things. If the definitions are crazy I can notice this when I read the paper. But if people use sensible definitions but fabricate the data I won’t be able to tell I am being deceived.
Can you really notice crazy definitions when you read papers? Did you notice this definition when you read this paper? Try reading the paper now, even with the hint and see if you notice it.
> “Isn’t this obvious?”
Problem is, insofar as it’s obvious it’s not true. Once everyone agrees psychoanalysis is terrible, then we get to say “Aha, all of those people in the old days were silly and believed in psychoanalysis, but thank goodness now we’ve fixed those loopholes, and it’s pretty much impossible to believe how anyone could ever have been so dumb.”
If we want people to *continue* to acknowledge the problem we’ve got to keep picking at precisely the examples that aren’t universally recognized.
CONSTANT VIGILANCE!
+[comically large number]
I would only add that IMO deliberate corruption of the institution of science would introduce very significant disutility all over the place, in unpredictable ways, so I don’t think that even the assurances you demand in the last paragraph would be enough for me to consider it acceptable.
The other side of this, though, is that sexism really is a pervasive problem in computer science that deserves addressing even if doing so would not increase the percentage of women in CS at all. Human decency and professional ethics should be enough to motivate action to address it; and it’s legitimate to worry that people will use statistics about differences in ability distribution as an excuse not to do so, however threadbare that excuse may be.
sexism really is a pervasive problem in computer science[citation needed]
What evidence do you have, other than the differential rate of employment, that sexism is a pervasive problem in computer science?
Certainly sexism exists, but is it really pervasive?
Also – many of the anectodes I’ve heard about sexism and “brogrammers” and such are not actually in computer science, they’re in ad-selling companies trying to be tech companies. So even if there are enough anecdotes to constitute data, are we talking about computer science, or are we talking about ad agencies where people do a little of their own programming, and keep some troglodytes in the basement to keep it all running?
The evidence I have consists largely of the experiences related to me and to the public by female friends and co-workers in my field, who have worked at a wide variety of companies, most of them definitely “real” tech companies and not “ad agencies where people do a little of their own programming”. There are a lot of these stories out there if you bother to look for them and listen to them; the problems they describe are far from universal but also far from rare.
What leads you to believe that sexism and sexual harassment are more common in tech companies or CS departments than in ad agencies, biology departments, or doctor’s offices?
Of course, they do not need to be more prevalent to address them, but you sound like you think these other fields have a magic bullet that CS has overlooked.
@Nicholas Weininger: The plural of anecdote is not data.
Forgive me for being flippant—I see where you’re coming from; I work in CS and I’ve heard these stories from my own female colleagues and I am certainly sympathetic to them. But as Anonymous points out, the presence of these anecdotes does not indicate that CS is worse than any other field. I think you are buying into an assumption that has been perpetuated by a small number of very vocal activists without a lot of real data to support it.
This article might be interesting to you.
Men in tech aren’t necessarily more sexist than men in any other field, but because tech is so male-heavy the women in tech are more likely to encounter sexism.
Did you read the first two comments to that article? The part where the author says,
The maths is right, but indeed it might well not apply to real life, but I’m not sure that makes it wrong
Because if that doesn’t make it wrong, it makes it irrelevant. And considering how clearly Gent originally intended his maths to apply to real life, I’m going to go with “wrong”. The analysis is based on an absurdly implausible model, and not backed up by any empirical data. It is worse than nonsense.
@John Schilling
Is this model plausible enough for you?
http://www.davidchart.com/2013/10/20/the-petrie-multiplier/
This one is even worse than the original.
1. The critical assumption is that neither men nor women will make sexist remarks if they are locally outnumbered. This is just plain wrong, and since the assumed 80/20 gender ratio means that women will almost always be outnumbered even a small probability of making sexist remarks while outnumbered will drastically change the results.
2. The results exceed the maximum plausible number of male->female sexist remarks, given the already-unrealistic model conditions, by about an order of magnitude. Not speaking python, I have not been able to find the bug leading to this error, but just the magnitude of the numbers should have been a warning sign to the author.
3. The model claims to allow men or women to make sexist remarks if their numbers are locally equal, but the use of an “elif” rather than “if” construction in the relevant logic only allows men to make sexist comments in such cases.
4. The author recognizes the aforementioned bug in his own comments, but dismisses it on account of “equal numbers will be rare”. Given the model assumptions, about the only possible opportunity for women to make sexist comments to men will be in one-on-one conversations where the numbers will in fact be equal.
5. Posting the results as socially relevant when you know there is a stupid obvious bug in the code, particularly when you know that the previous version of the analysis was mathematically shaky and you are trying to rescue it through greater rigor, is nigh-unconscionable.
I suppose I could try to write up something non-buggy in C++ and using less absolute and absurd assumptions. Or I could note that, between Leslie et al and the various incarnations of the Petrie Multiplier, it’s looking like not only are girls fundamentally bad at math but they are highly contagious. Neither of these really appeals, so I’m going to go work on engineering problems that are actually fun and useful. But the next time I hear about the “Petrie Multiplier”, it had better be in a peer-reviewed journal.
Yeah, you’d better run and hide before my girl cooties annihilate your C++ skills.
@John Schilling: Good points, but your last paragraph was rude and uncalled for. You might also want to consider that both of the blog posts in question were written by men. I’ll give you the benefit of the doubt and assume you were trying to be sarcastic, but it came across very poorly.
@Pseudonymous Platypus
Of course John noticed that. That’s what the “highly contagious” bit was about. Apparently, those poor gentlemen lost a dozen IQ points after spending too much time with “girls”.
It means that science can be really really easily corrupted for political ends
Why are you surprised by this? The Goddess of Reason is a metaphor, not an actually existing deity. Science is not some untouchable ideal Platonic Form existing in true reality above the grubby sub-lunary world, it’s a process carried out by, performed by, done by humans.
And humans do all kinds of stupid, tribal, caving in to pressure things.
I also am not sure how to solve the problem of the gender gap in mathematics. Do we leave it as it is? Then we run into the problem of men getting the high-status, high-pay jobs and women being relegated to the unimportant fields like sociology – and it’s not a matter of science here, it’s a matter of humans and how we structure our ways of living and being.
– Smart people go into the high end fields which give big rewards, the more demanding the work the bigger the reward and the difficulty and demands justify the corresponding rewards. Maths and related fields are high end, men are more likely to be better at maths, men are the high status gender. That’s how you end up with a caste system. It’s not intentional, but it’ll be how it works: the lustre reflected on all men from the objective scientific truth that some men are intelligent enough to pursue mathematics at a high level, and that there are more of these men than there are of these women.
– Increase intelligence in general? But again, unless you specifically increase intelligence for maths, you’re not solving the problem. More genius art historians is not what you want.
– Which leads on to increasing intelligence in women such that they’re intelligent in the same way men are intelligent. Oh, boy. Who wants to touch this one? Making women into pseudo-men? That’s like the old ‘compliment’ that “Why, you think like a man!” C.S. Lewis said this to his future wife, Joy Davidman, who not unnaturally returned “Why do you think that’s a compliment?”
Smart women are only smart if they’re smart about the same things in the same way a smart man is smart?
– Intelligence research is going to come out that some people are not as intelligent as others. Well, stating the obvious there. Where we are going to have huge problems is with the “natural inferiors” that this will engender. Your solution is to work to raise up everyone’s level of intelligence, but why? Is there any point to making a road sweeper a much smarter road sweeper? Simply classify these people as not full humans and let nature take its course to wipe them out if they can’t compete and keep up with the requirements of the modern world. Why waste resources on making the children of Joe the Auto Assembly Line worker (whose job is now done by robots) a bit smarter which only makes them ‘very high average’, when the same resources could go to making the children of Lionel The Physicist a little bit smarter and tip them up the genius scale even more?
>Is there any point to making a road sweeper a much smarter road sweeper? Simply classify these people as not full humans and let nature take its course to wipe them out if they can’t compete and keep up with the requirements of the modern world.
Did you sit down and think about it for 5 minutes before writing off the problem as obviously intractable, or did you already have “raising intelligence is useless” as your conclusion and worked backwards?
There aren’t only two options here.
Well, I think Scott mentioned elsewhere in the thread that he’s worried that praising hard work instead of genius could leave us without enough genuises to address existential risks.
In this context, Deiseach’s suggestion of pouring all resources into the smartest kids makes perfect sense. It’s a matter of survival, after all.
Developed countries currently have systems of support for people who are demonstrably too disabled to find regular employment. I’m not sure why you expect that to change and to let “nature take its course to wipe them out” when the disability becomes an IQ of less than 120.
“I also am not sure how to solve the problem of the gender gap in mathematics. Do we leave it as it is? Then we run into the problem of men getting the high-status, high-pay jobs and women being relegated to the unimportant fields like sociology – and it’s not a matter of science here, it’s a matter of humans and how we structure our ways of living and being.”
I think you’re overestimating the prestige and wealth of STEM jobs. Do they represent more than a tiny percent of the high-status opportunities available?
Women are already > 50% of college graduates, and already earn more than men at the same stage in their lives. They’re already > 50% of biologists. They’re approaching parity in law and medicine. I feel like “engineering, computer programming, and a couple of research positions in physics” is not such a huge slice of the high-prestige pie to be hugely interesting. If women became equal to or better than men at politics and business, would we really be complaining that there aren’t enough female mathematicians, any more than we’re complaining now about male nurses?
(I’m not sure if there are hard biological limits on making women equal to men in politics and business. I suspect not; there seem to be more top-level women politicians (Thatcher, Warren, Clinton) than top-level women mathematicians, which suggests there’s no variance differential.)
– Your solution is to work to raise up everyone’s level of intelligence, but why? Is there any point to making a road sweeper a much smarter road sweeper?
First of all, yes. I think there’s something good in itself in having road sweepers who read Dante and Aristotle and debate quantum theory on their days off. Not to mention road sweepers who always vote for the best candidate in elections because they’re too smart to be fooled by propaganda.
More realistically, if we raise everyone’s IQ, even the road sweepers, we’ll probably be catalyzing technological progress to the point where robots will sweep our roads and we’ll either find something better to make road sweepers do or else be able to give them leisure time.
More realistically still, from what I hear from people in the field, once we really understand the nuts and bolts of intelligence, it will be as easy to increase IQ two hundred points as it is twenty points. Once our road sweepers have IQ 300, it’s not just that there won’t be road sweepers anymore. There won’t be roads. At that point we’ll be teleporting wherever we want to go, assuming we’re still stuck in the time-space continuum at all.
I may be exaggerating slightly, but it will be closer to that scenario than to the “road sweeper reads Dante but continues sweeping roads” scenario.
Which field? And might there be an article or two the rest of us could look at?
Yes, please do share. I am interested in this topic and would (continue to) subscribe to your newsletter.
You know, back in the 70s, there were futurologists predicting that by the far-flung days of the year 2000, we’ll all be working five-hour work weeks and have so much leisure time and money, we wouldn’t know what to do with it.
Has that come about? Or, as Larry Summers said in that speech of his quoted in a comment above, do you need to be “thinking about the job eighty hours a week” if you want to be the high achiever who gets places?
I’m quite sure we’ll replace road sweepers with robots at some time; we’re doing a lot towards pushing mechanisation of blue-collar work even in places like the pharmaceutical industry, where instead of an assembly line of workers you now have one guy overseeing the automated process.
But there’s going to be a gap between the unemployed road sweeper of today and the genius former road sweeper of tomorrow, and that’s what I’m talking about. Didn’t we already have a conversation about the economist Robin Hanson and his alleged statement that difficult people don’t necessarily have a right to exist? There are nine billion people on this planet, and I’m sure I’m not the only one who has seen people willing to state we should be reducing the surplus population as a matter of urgency.
Ten years from now, forty year old Mike will be replaced by a road sweeping robot. What does he do? He’s pretty much unemployable, no matter what training schemes he has to go on to prove to the social welfare department that he’s genuinely looking for work. Unless we have the magic injection that will make Mike a genius level person who can now start studying physics, what happens to him?
And I’m quite sure there will be those wiling to argue that the Mikes of the world are being swept away by natural forces, and it’s a waste of time pulling up his kids (who inherited his deficient genetic intelligence – after all, if he was really smart in the first place, he wouldn’t be a road sweeper) a few points up the IQ scale. That takes too long. Put the resources where they’ll do the most good! Find the naturally smart kids, pump resources into them, let them have smart kids of their own – and let the deficient surplus population quietly die off.
Deiseach, serious question. I keep reading your comments in which you imply that your political opponents believe that a significant fraction of society are basically some kind of Untermenschen who need to be either permanently enslaved or exterminated. And, well, I’ve never run into anyone who actually thinks that.
Is the Overton window really different in Ireland? Or do you think that most conservatives secretly believe this even though they claim not to? Or is it something else?
@Nita
Naively I would guess Scott’s talking about the research areas that Steve Hsu tends to write about?
My basic model from reading abstracts and watching videos of research talks (over a year ago, so maybe other people’s models have clarified since then in response to better data) is that brains are constructed by lots of genes and when a few genes go awry they become less functional but still basically work. There are tens of thousands of ways for brains to break down like this, and each way reduces IQ a little bit.
Basically all humans have many such slightly broken genes (in a unique pattern), losing fractions of a point here and there, but people who are “smarter than average” have slightly fewer.
Once we’ve figured out all the ways that brain genes can be “misspelled”, it should be theoretically (if not pragmatically) possible to produce human genomes with no broken brain genes… “locally modal genomes”… like running spelling correct on a document. Rough calculations suggest that a brain produced by a “fully spellchecked genome” would have an IQ of ~300.
Aside from this potentially being economically costly, and politically infeasible, there might be a “real” barrier to this in that real genomes are often full of compromises, often in response to diseases. Europeans have mutations to fight tuberculosis (a double dose of which gives cystic fibrosis) and Africans have anti-malarial mutations (a double dose of which gives sickle cell anemia) and so on. Losing a few IQ points to avoid a terrible disease can be worth it, and a 300 IQ spell checked genome might end up susceptible to everything, and thus be a pragmatically losing proposition?
Evolution is pretty clever. Doing better than it will take serious work 😛
Nita, the topic is mutational load and the book to read is Mutants by Aramnd Leroi. I don’t think it talks specifically about IQ, but that’s not the part that confuses people.
Thanks for the recs, JenniferRM and Anonymous! I had heard of the “genome spelling check” idea, but I still wonder where the estimation of IQ 300 came from. To me, it’s like a claim that fixing gene errors will make everyone 9 feet tall.
Huge numbers like 300 come from Steve Hsu’s blog, that Jennifer cited. But they really come from the idea of mutational load, which is why I suggest Leroi.
It is common for selective breeding to move a trait 30 standard deviations. It would be easy to breed humans that are 9 feet. It is unlikely that one could easily move human height 30 standard deviations, but it is probably easy to move weight 30 standard deviations. That means that in the population before breeding there exists variation enough to move 30 standard deviations. If the trait is mainly controlled by mutational load, then spell-checking the genome should move it the whole way all on its own.
IQ 300 is meaningless. What it really means is that one could find in the typical individual 4 sets of variants, each of which, when corrected would yield IQ 150. It is not clear what would happen if all 4 sets were corrected. It might have bad effects, since the brain is designed under the assumption of mutational load. This concern is more plausible in the case of height than IQ.
Steve Hsu gives various models and reality checks. There is no direct measurement of the mutation load hypothesis. But there has been fairly direct measurement that no common variant contributes more than 1/100 part of the variance, probably not even 1/1000. So there must be lots of relevant genes and it is hard to find a model compatible with that that does not predict that everyone has many bad variants.
If the conclusion that the geeks are evil and deserve to be punished was derived from the studies you are critiquing, and the authors did not realize the mistakes they are making – then your critique would be relevant and important.
But if these studies were intended as merely additional support for the conclusion already established by other means – then Nil is correct. Who cares?
Cutting down supports for a structure makes it more likely to fall EVEN IF those aren’t the most important supports or the ones that the structure was built on. Notice how people fighting against the belief that black people were subhuman, which was probably just a convenient excuse to enslave them and take their stuff just like many similar excuses in history, has resulted in broader civil rights.
There’s also the other issue here, which is that if we start building supports for a NEW structure of acknowledging intelligence differences, we can start to improve intelligence in a much more systematic and effective way.
Suppose science journals were publishing terrible, easily disproven articles saying that Jews were an inferior race.
Now obviously that conclusion would not have been derived from the bad science. It would just be additional support for the conclusion already established by other means.
But it would still be worth nipping in the bud.
Hm, I’m getting an impression like this:
Leslie et al. [paraphrased]:
“Hey, let’s tell kids that hard work is very important in maths, philosophy and music composition.”
Scott [paraphrased]:
“If nerds were Jews, you guys would be Nazis.”
What am I misunderstanding? (Full disclosure: I sincerely believe that hard work is indeed extremely important in mathematics.)
Deleting duplicate post
Interesting choice of example.
Correct me if I am wrong, but I am guessing you chose it because publishing bad things about Jews had led to very bad consequences.
In that case it should not matter where the science behind such conclusions is good or bad. You should be agreeing with Nil.
@Nita
Leslie et al argues that women don’t do well in science because people don’t expect them to do well in science. Which is a very dubious result as Scott so painstakingly analyzed.
And I (speaking for myself) am annoyed that people use this as a weapon to beat nerds over the head with. Obviously women don’t do well in science because those nasty misogynistic fedora wearers are providing a hostile environment for them and we need to put them in their place.
I assume the Jew analogy is because Jews were disliked in the early 1900s partially for similar reasons
Also all of the following are compatible:
Hard work in important in mathematics.
Innate ability is important in mathematics.
No amount of hard work is sufficient for success in mathematics.
The gender gap in mathematics is not due to a difference in innate ability, hard work or discrimination.
I think the first three are true, and the I have no idea what the cause of the gender gap is, except that it probably isn’t discrimination.
@Alexander Stanislaw
Leslie et al. explicitly argue against the stereotype of STEM as a bastion of sexism:
From the graphs, their top 3 of “genius” disciplines are:
1. philosophy (by a huge margin)
2. maths (by a smaller margin)
3. music composition, literature, physics and economics (pretty similar)
The average students of sociology, political science and art history consider their field more demanding of special talent than the average student of molecular biology.
So, downsides of the study:
– awkward handling of the selectivity hypothesis
– conflating field-specific “talent” with general “brilliance”
Upsides of the study:
– using actual statistics instead of handwavy arguments so popular in blogs and the media
– showing that STEM nerds aren’t especially smug
They propose three mechanisms for the influence of “FSAB” on the percentage of women. Two of those three are internal and 100% compatible with zero discrimination in the fields.
And yet, to you and Scott, this is a piece of evil anti-nerd propaganda?
Re: Untitled. Marcotte and Penny accused Aaronson of romanticizing arranged marriage in shtetls and similar self-centered ideas. I’m not sure what that has to do with IQ, PhDs or field-specific talents.
Nita: That has nothing to do with why I wrote the post above. Someone made the claim “It doesn’t matter if a study unfairly disparages a group if the group was already unfairly disparaged.”
I am providing evidence that this is false. You are misunderstanding me and rounding me fof to something horrible and inflammatory.
Okay, I was wrong.
Person who hates all things good (and puppies) here: can confirm we gloat about our evil plans to do this over scotch and kitten blood at the Shadow Republican National Convention.
In all seriousness though, congratulations. This entire topic has become so enraging that
I can’t even think about it without my mental narrative sounding like Mr. doubleplusungoodthink above. That you can pass enough sanity checks to talk about it rationally is amazing.
I honestly haven’t ruled out differences in socialization starting as early as elementary school. If that’s true, then all of this talk of sexism in math departments is a giant distraction that’s not helping women and which is giving cover to the real problem
I honestly believe that “sexism in mathematics departments” is one part of “socialisation starting as early as elementary school”. Not in their admissions procedures but in the way that they present mathematics. For instance “kindergarten teachers think men are better at maths” might have something to do with those teachers experiences of mathematics departments while they were studying to be teachers? Obviously there are many parts, but I think this is one.
I think that the “this is not innate genius” thing mostly comes down to arguments about the meaning of “innate”; if early socialisation is important then perhaps its effects can be undone by later hard-work? But if one believes simply “I’m bad at maths now, I will be bad at it forever” then there is no incentive to try to undo the early damage through hard-work now.
But the teachers aren’t in the math department, they’re away in their own little department.
I find your last point very interesting. I’ve sometimes mocked people’s proposed solutions to politically contentious issues as essentially saying “If everyone was really smart, it’d work itself out.”
But of course, my cynicism is unproductive. Your idea is much better.
“Moderate positives”?
Knowing what’s in this post may be little better than never having noticed the gender gap at all, but that isn’t an option. If we notice the gender gap and don’t know this stuff…
The obvious thing is to tweak the admission standards at every phase of the pipeline to get more balance. You don’t need to do it explicitly. Just pick out of dozens of potential metrics the one that gets the most even gender balance. This means getting less qualified people.
Or we can do what the article Scott replied to suggested: spread the idea that intelligence is a myth and hard work is the only thing that matters. Now people will self-select into the wrong fields.
If this means our philosophers are less qualified than they could be, that’s an acceptable cost.
But if that means our engineers are less qualified than they could be, that’s an existential risk.
If selecting bioengineering Phd candidates suboptimally delays an AIDS cure by one year, that’s 1.5 million people dead.
Unless that year is the one in which a bioterrorist finds a way to cross AIDS with influenza. Then it’s all the people dead.
Why is the assumption that gender balancing a field will pick the less capable?
I have a class for Really Good Engineers. There are 50 places. Gender balance on the usual way means there are 35 men and 15 women. I want more women in my class.
You say “Making it 25 men and 25 women means we take on an extra 10 less capable women at the expense of 10 more capable men”.
Or we could spread our nets wider. Say in every batch of 200 college applicants there are 120 smart guys and 80 smart women. Let’s keep sorting through the batches until we get our 25 smart women who are just as good as the minimum smart requirement for the smart guys who would have got the places. Maybe our 25 women are just as smart as the smartest guys! We just need to sift through a larger number of applicants to cherry pick the ones we want!
Is that fair to the larger number of qualified male applicants who will be rejected in favour of the women? Maybe not.
But that’s a different question to “We have to take the first 25 women who apply, regardless of whether they’re as good as the men or not”. Evening out gender balance need not mean taking less able candidates, unless your application pool is really small.
Is it that small, or are you only settling for the first 100 men who apply and not willing to sort through extra applicants?
That works if you’re the only person in your culture doing it. If you’re not, then every female applicant you take makes every other hiring manager’s diversity requirements incrementally harder to meet.
Depending on how and whether hiring managers choose to cooperate with these ambitions, this may or may not bottom out in unattainable expectations — but even the attainable ones don’t look good. It might give you a mix of egalitarian and even more male-dominated workplaces, or it might mean that some of them cut corners somewhere and end up with less qualified women. The only real escape here is if that link from the other day was right and women make groups perform better for reasons other than individual ability — but that could be rephrased as “the hiring criteria are wrong”, which feels like it dodges the point.
Spreading your nets wider has a cost. And given a particular expenditure of money and time that you are willing to make to get good students, and assuming there is no significant sex discrimination, you will get better students if you just search for talented and eager students regardless of sex. Adding the constraint of having at least x% women is either irrelevant (if x is less than the percentage of women which would obtain naturally) or will reduce the quality of your students.
Someone needs to recite the Litany of Tarski and reflect upon the nature of their sins against reality.
This knowledge cuts to the very heart of the issue of whether “business necessity” is a valid defense against an accusation of “disparate impact.” I don’t intend to deny people the evidence required to defend themselves because it makes *you* uncomfortable.
How Rational of you to recommend reciting Litanies and repenting sins.
That’s a pretty cutting remark, since as well know, rational behavior is universally dull, uninspiring, unemotional, and uses only difficult scientific jargon disconnected from its cultural milieu. This is why the only rational course of action is to be a tedious, bespectacled pedant under all circumstances.
The “Litany of Tarski” makes no sense within the larger context of a rational worldview. The litany very clearly says to “do X” regardless of the consequences. This is almost never rational advice. One should care about the consequences. The exception is advice like “do not take power, even for the good of the tribe.” In which case the refusal to consider considers serves a safeguard against rationalization. But these cases are exceptions and one needs to actually argue for them.
The claim that the poster should “repent” is transparently shaming someone for the crime of actually thinking.
I think the distinction you’re looking for here is “epistemic rationality” (i.e. slavishly following the litany of tarski, to a first approximation) vs. “instrumental rationality” (t.a.f.a., systematically succeeding at more general goals). Note that the Litany of Tarski seems to be very useful from an instrumental perspective, if not 100% universally applicable. I guess the point at issue here is whether it’s worth taking on the litany full-throatedly in the spirit of rule utilitarianism, and if not, how grave of circumstances should be the threshold for abandoning its counsel. I don’t have exact answers of course, but I would certainly say I lean more towards Anon’s view than you seem to.
(apologies for the lengthy of rebuttal of not-your-point in the grandparent, by the way. I clearly misunderstood your original comment.)
Looks like someone is a Vulcan rationalist.
If you believe that the negative consequences of everyone knowing the truth about X exceed the instrumental value to you of knowing the truth about X, and that you can’t know the truth about X without everyone else knowing, you actually don’t want your beliefs about X to be made more accurate. If nil doesn’t think that the efforts that would be necessary to know everything relevant about gender differences in intelligence while hiding the data from everyone else are worth it to him, he actually does not desire to believe that gender leads to inherent differences in intelligence, even if gender does lead to inherent differences in intelligence.
I’m not sure how reciting a statement that is actually false in this case would be useful to anyone.
Others have made idealistic objections to this viewpoint, so allow me to make a practical one: Truth, by its nature, is hard to suppress. No matter how fully you think you can control public discourse, there will always be dissidents willing to do what Scott is doing here, and stick their necks out by supporting a politically incorrect truth. Most of them will not be as “friendly” as Scott, either — think e.g. redpillers. What’s likely to result is a scenario where most people profess to believe the mandated consensus, but actually believe the dissidents. The same dynamic has happened even in very extreme “mandated consensus” situations like the former Soviet Union.
The act of attempting to mandate consensus may strengthen the very bigots whom you (and I, and probably most people here) would, politically, most like to defeat.
“Truth, by its nature, is hard to suppress. No matter how fully you think you can control public discourse, there will always be dissidents willing to do what Scott is doing here, and stick their necks out by supporting a politically incorrect truth.”
So you are aware that Francesco Bruno was not, in fact, a Champion of Rationality and died because he was a heretic that thought a sun-centric solar system was more aesthetically elegant, right?
Just as an example.
“The truth,” by your limited definition, has been “surpressed” quite successfully and quite often throughout human history.
According to Wikipedia, Francesco Bruno is an Olympic shooter. Presumably you’re thinking of Giordano Bruno.
I do wonder how many SSC readers are familiar only with the Cosmos version of his life story, versus how many have heard more accurate versions of events from other sources (such as the proliferation of critical online articles published after Cosmos premiered). It would tell us something interesting about where we tend to get this kind of information from.
‘Bruno’s heresy was woo-woo pseudo-theology, and the shape of the universe was not a theological issue.’ — tl;dr from TOF
‘The Church’s quarrel with most of the astronomers around that period, was that they were presenting their theories as facts, rather than as what our scientists call ‘models’; the old way was to say here is one way to account for the data, but there may be others.’ — tl:dr from C.S. Lewis, The Discarded Image
I’ve really enjoyed the discussion this comment has engendered. I would also like to quickly point out that this argument has been voiced publicly by John Horgan in a blog post called Should Research on Race and IQ Be Banned? Spoiler: he answers in the affirmative. He also quotes no less than Noam Chomsky on this issue:
So, the argument that such knowledge has no value and may be socially harmful is hardly new.
Personally, I strongly disagree with Horgan and Chomsky, and am disturbed by the implication that only racists and sexists would care about the subject, which attempts to create automatic prejudice against anyone with an honest desire to do research in this area. I support those who have argued (cogently in my opinion) that true knowledge is preferable to ignorance.
So here’s a really frustrating thing. In a lot of more abstract fields (CS being a notorious one, and also my field so I’ve seen this myself) there is, in fact, a pretty strong culturally transmitted Genius Bias. And it probably does affect what kinds of people go into these fields, and not necessarily for the best because perception of genius depends on a lot of things other than innate-ability-as-it-actually-affects-relevant-outcomes, and even plenty of people who do find success in these fields find it grating, and I’m pretty sure that this is all deeply connected to sexism one way or another.
But, as this statistical analysis reminds us, reversed stupidity is not intelligence.
I think there’s a memetic prevalence debate here. Highly-educated-liberal-society needs to stop putting its collective fingers in its ears and shouting “BLAH BLAH BLAH I CAN’T HEAR YOU” every time the numbers show that innate ability affects outcomes. But our cultural sphere focuses on it a little too much to the exclusion of other factors.
There’s a third factor that both sides tend to ignore – simple preference that is not driven by either ability OR prejudice.
Based on my test scores, I’m equally good at Language skills and math. I have no doubt that I could have done well in English, history, law, or psychology, but I went into engineering because it was more interesting to me (I’m male, FWIW – English and psychology are female dominated but history and law are not).
The Mathematics section of the General gRE seems like an extremely poor measure of innate ability. The test is fairly easy. And the act of studying a math* degree is very good practice for the Quantitative GRE.
A better proxy would be scores on the MAthematic sSubject GRE. Idk how many people have taken it but its rather challenging. The Mathematics subject GRE focuses mostly on calculus and to a lesser extent linear algebra. The questions on topology and abstract algebra (not “advanced” subjects) are always among the asiest on the test. However the calculus questions are difficult and you are under extreme time pressure of only 2.6 minutes per question!
Most mathematics students do not spend much of their time learning how to do difficult calculus problems fast. One can prepare for any IQ test. But doing low level problems very fast seems like something that rewards “g” to a large degree. In addition most math grad programs claim that ignore the Quant GRE score as the test is way too easy. But they openly care about the subject GRE score.
*or CS or physics
I would honestly only be convinced if you could somehow regress majors in undergrad/grad against at least IQ. Better would be Weschler and Raven’s progressive Matrices would be ideal. I know SAT scores are correlated strongly with IQ. But I would really want evidence that the correlation between IQ and SAT are roughly the same in the sample we care about (people with a real chance of getting into PHD programs) as in the general population.
I do not think this is an isolated demand for rigor. GRE Quant just seems like too poor of a measure.
Apparently there’s enough variation on the quantitative general GRE to generate the dispersions Scott analyzes. I think that’s good enough.
Using the Math subject GRE is going to be more skewed, because, while it’s better at discriminating between “brilliant at math” and “merely very good”, your population of test takers is already going to be pretty biased toward people who want to go into math-related fields and probably scored high on the general quantitative GRE. Much less representative of the general grad school applicant population.
The problem with the math subject GRE is not how many take it, but who: people applying to math grad school. It tells you nothing about different subjects. (Maybe it lets you compare pure math to applied, but I don’t think that ETS even asks that distinction.)
Why do you claim that a math degree is good preparation for the quantitative GRE but poor preparation for the math subject GRE? They are both timed tests of calculus, just one is easier than the other. (except for the easy questions on topology and abstract algebra, which are simply questions of whether you studied pure math, which is not what we want to know)
Well one could use the Subject gRE scores a check for discrimination. If possible find the percentage chance a person with a Mathematics GRE score of X gets into say a top40 school. Then keep the percentage chance a woman with a score X gets into a top40 school. I am almost certain this will actually show positive discrimination in favor of women.
The Quant GRE has almost no ability to discern between people with even moderate mathematical talent. IQ scores are known to be predictive of many things. And we know with confidence exactly how they are distributed. One can of course study for IQ tests but the effect caps out for most people. The size of this effect is also well understood. So I would personally want to see IQ (or as stated ideally Raven’s Matrices) as the measure of innate talent.
Though I think subject GRE would suffice as a metric to do a check for discrimination. Given how easy it is to get a very high score I don’t think the quant GRe score is useful.
A little nitpicky but the GRE
“does not include trigonometry, calculus or other higher-level mathematics”
https://www.ets.org/gre/revised_general/prepare/quantitative_reasoning/
Having taken it I wouldn’t consider it anything more then a 5 hour boredom challenge.
Thanks!
Maybe that’s not a nitpick but actually Stargirl’s meaning: that science majors spend time practicing calculus but not practicing high school algebra. (And now that I understand the claim I can respond to it. I reject it: doing calculus involves practicing high school algebra.)
FYI your link to the GRE stats spreadsheet is broken (at least for me).
I am VERY skeptical of any results involving the GRE quantitative test. The version prior to 2011 was from 200-800, and was highly skewed to the right. It had a 50th percentile score of 670, and 75 percentile score of 750 [0]. The amount of math people take in college varies widely and no test of quantitative ability is going to have a normal distribution when it’s taken by STEM and non-STEM individuals.
The new scoring system is allegedly normal, but I’m skeptical that such a thing is possible (or desirable) given the effectively bimodal distribution of test-takers (STEM and non-STEM). Also, it’s not clear to me how much they actually reformed the question content versus the scoring system. A few questions can make a HUGE percentile difference, that may be how they forced it into a normal distribution [1]
>graduate programs accept applicants based on their innate ability as measured in GRE scores
GRE tests absolutely do not measure innate ability, nor are they designed to. They are typically taken near the end college. So (at best) they measure innate ability + education. For quantitative scores this has an immense impact. The exact same person will do much, much better on the GRE quantitative section if they majored in math (or any STEM discipline) than if they majored in art history. Not only do they have extra mathematical education, they’ve been using they’re math skills for years instead of letting them atrophy.
Qualitatively similar objections could apply to the SAT data; there are differences in the classes people take in high school, and how much work they put into them, as you mentioned. I would expect them to be quantitatively smaller though (as seen).
[0] https://www.ets.org/s/gre/pdf/concordance_information.pdf
[1]New GRE Scores: Scales and Percentiles. http://gre.kaptest.com/2011/11/07/553/
The GRE doesn’t measure innate ability, but it doesn’t have to for this analysis – it just has to correlate. And the overall evidence seems to suggest that it does. And, most importantly, it correlates better then “perceived ability”, which is the whole point of this post.
I fixed the spreadsheet link. Thanks for telling me.
Quantitative GRE correlates at > 0.7 with IQ, which makes me think it’s a decent innate ability test despite the very real problems you mention.
It’s decent, but is it good enough to distinguish between actual ability and self-perceived ability (which has an effect on what classes you take)?
The study those numbers come from is:
Carvajal, H., and K. K. Pauls. “Relationships among Graduate Record Examination scores, Wechsler Adult Intelligence Scale-Revised IQs, and undergraduate Grade Point Average.” College Student Journal 29 (1995): 414-416.
Which doesn’t appear to exist online. I see no mention of separation by field, so I’m guessing the same problem bi-modal problem exists. The correlations are likely very different for STEM and non-STEM majors, and throwing them together will be misleading.
Also I realize I misunderstood your usage of the term “innate”, but in my defense, your usage is non-standard. “Innate” typically means “born with” (which is still not exactly the same as genetic because stuff can happen in the womb but it’s much closer).
That usage of innate is not Scott’s, but Leslie’s.
It might well be the case that Leslie chose that definition to force anybody disputing the conclusion to sound like they’re arguing that people who do well in math are just born that way, deal with it.
Somewhat relatedly, Steve Hsu has some great data on how the preferences of high-math-ability girls differ from the preferences of high-math-ability boys: http://infoproc.blogspot.com/2014/11/gender-differences-in-preferences.html
Even after ability is controlled for, the group differences in the priorities of men and women can be quite significant.
This blog is the biggest breath of fresh air I’ve encountered for a long while. Finally someone talking sense about the social sciences…
I think GRE is a poor mesure of innate ability. The quantitative GRE is not very high level, it is mostly just algebra. If you lacked the ability to do well on it, it would be impossible to pass senior level engineering courses. The horizonal axis is a better proxy for the amount of math used in the undergrad degree than for the innate ability, since after 4 years of practicing math, you would be pretty good at it.
Once again, this is why I ran the same analysis with SAT scores.
W.R.T. footnote 6, has anyone tried doing a gender vs SAT regression with the data points weighted by population? That would solve the problem of giving tiny vocational majors undue influence.
Here you go. I started with Scott’s spreadsheet which I guess was made from these SAT scores of prospective majors and these sex ratios of conferred degrees. I weighted by the populations in the first link.
Very off topic, but I just wanted to say I arrived at your blog for one of the online drama dustups you were involved in, and I’ve stuck around because I’ve appreciated your depth of analysis, assumptions of good faith in discussion, and willingness to give multiple viewpoints consideration. You posted at one point you were worried you would only be known for the posts that incite drama, I wanted to encourage you that that might actually be what gets people in the door.
I’m not on the same page as you regarding the singularity or ai risk(I greatly enjoyed Moloch, but I reacted to the conclusion similarly to how I would have reacted to a Christian saying the answer to the trap is God. I’m afraid it’s a leap of faith that might distract us from other solutions). Even so, I feel yours is a perspective I want to hear even when we disagree. I genuinely feel like you’re raising the level of discourse. So, thank you. Please keep it up.
Re: AI Risk. For some “historical” background, Scott used to post on the website Lesswrong, which was founded + had most of its core content written by Eliezer Yudkowsky, who feels very strongly / has thought a lot about the issue of AI risk. The “core content” is a long series of lengthy, idiosyncratic and self referential synthesis of cognitive science, metaphysics and epistemology.
I mention this just to point out there is a *very* big information divide between why Scott might believe AI is an issue vs people who might generically find his writing interesting, and that it is laborious to even begin reading the basis of his reasoning. Yes, this is similar to the “oh yeah read our Holy Bible and some–increasingly-obscure-subset-of-theologicians before you dismiss us” rebuttal but…
Nick Bostrom’s Superintelligence is probably a more succinct and less… I guess weird introduction to the subject. (Note: I have not read it myself, others should gleefully mock any inaccuracies in that impression).
If you’re interested, and no one yells at me for being wrong in this subject, I encourage you to buy it through Scott’s amazon referral thing. You learn about a different point of view, Scott gets happy that he got paid and probably writes more posts and I get paid off by the SSC zaibatsu[0].
[0] In Elua pull-my-string dolls.
I have read Superintelligence(while being new to the subject) and thought it was a pretty good introduction to AI risk.
I just wanted to chime in here with another data point. I also found the blog because I was linked from elsewhere to one of the controversial posts.
It might sound strange, or hyperbolic, but this blog is making me a nicer person. The way Scott argues both sides has had a huge effect on how I talk to other people online. It started as realizing that I found Scott’s charitable writing style persuasive, and I wanted to be persuasive so I emulated this style, but in the process of trying to persuade people I accidentally became a more emotionally open person who focuses less on trying to hurt bad guys with my words.
I got in a discussion earlier today that was tangentially related to being kind to internet strangers in discussion. I went over my reddit comment history over the past month that I’ve been coming to this blog, and I was amazed by how noticeable the difference in my behavior to others was! Normally, I’d say I end up regretting at least half of what I say on the internet. It’s not that what I say is wrong, but I use my intellect to demean and humiliate others instead of as an opportunity to grow and learn new things. Well, I read the things I’ve said over the past month and I didn’t feel that “who said this” emotional dissonance, weird vague shame feeling, I felt proud of how I handled myself.
I know sometimes the tail end of our good deeds take place out of sight, so I hope Scott reads this and realizes that he probably has a positive impact on all kinds of people that he doesn’t even know, in ways that he probably would never guess.
One question in the “further research if everyone has infinite research resources” file: do GRE score differences which are attributable to gender have the same predictive power for how well someone will do once someone is actually admitted to a program as GRE scores attributable to within-group variation? (Or less? Or more? Varies by subject?)
So, is the title of this post a deliberate attempt to make it less likely to go viral?
I’m hoping it keeps the Atlantic at bay for a little while 😛
I did have to resist the temptation to call it “Perceptions Of Required Ability Act As A Proxy For Actual Required Ability In Explaining The Gender Gap, Motherfuckers”
If you wanted to go the other way you could have called it
“This blogger used a weird trick trick to totally debunk “muh gender gap” myth. Feminists hate him.”
Why does the SATMath graph end at 620? This seems to be a pretty average score to determine high end mathematical skills. Maybe I am missing something.
I think we all suspect that coming to a conclusion that genetics plays a significant role (or even a measurable role) in intellect is the third rail of the social sciences. I suggest there is an enormous amount of confirmation bias present as 100x more energy is put into disproving this theory than proving it.
I just wish someone would put an end to the interpretation of the SAT / wealth correlation. It sure looks like cause and effect are getting reversed in the current politically correct interpretation. The anti-test crowd quotes this ad naseum.
I think the SAT graph ends at 620 because that’s the math score in the highest-math-score major, so there are no data points after that.
Damn, Scott, good work… you should write this up and send it to Science Magazine as a comment on the original article.
Seriously.
First, this is kind of an important topic, and setting things straight is definitely worth it (even if your position is of the “dog bites man” type that tends to get less press than “negative expectations by humans cause aggressive behaviour in canines” would); second, getting a snarky comment on a shitty paper published can be a very rewarding experience; third, maybe seeing a paper get demolished in public makes authors a little more hesitant to submit halfbaked bullshit in the future. (Probably not, but a man can dream…)
I agree; this is a solid, well-considered and well-documented response. It deserves to be published.
I’m not going to do this because it sounds like lots of work, I doubt it would get published, and I don’t really know how to do academic writing.
But if somebody else thinks they’d publish it, and wants to get a free publication, they’re welcome to contact me about writing it up and splitting the credit. Contact me at scott[at]shireroth[dot]org if you’re interested.
(or blame, as the case may be)
I’m not in the business anymore, otherwise I’d take you up on that offer; I hope someone else does. As far academic writing goes, I’m sure you could write much better papers than most academics. Cut down on the snark and the jokes a little bit, throw in more footnotes, add a redundant abstract and conclusion, and you’re almost there.
This subthread raises a question of interest to me: To what extent are online discussions such as this going to replace the conventional print media scientific exchanges? I’m a professional academic, and I would certainly give more weight to Scott’s posts than to the random published journal article.
” I’m a professional academic, and I would certainly give more weight to Scott’s posts than to the random published journal article.”
Me too.
My understanding of early scientific research was that a lot of it was linked through informal friendships and letter-sending rather than through formal journals and institutions.
I’ve wondered if over time, at least in some fields, we’ll see the best researchers corresponding through blogs and informal online chains of communication, reproducing these earlier conditions. (I also wonder if journals are trying to formalize what makes a thing be “good work” in a way unformalizable; “…the primary thing when you take a sword in your hands is your intention to cut the enemy”, etc)
(On the other hand, at least 40% of my knowledge of early science and math is from reading books in the Baroque Cycle, so I also wonder if my impression of early science is correct.)
I am curious if people think there are currently any fields at all (even small subfields) in which the best work has been done through informal means, by bloggers, on forums, etc. Can anyone think of anything?
I recently read a great article about the Volokh Conspiracy that posits that this sort of thing is already happening in the field of law, around commentary that an article on Conspiracy is more influential than in most law journals. You’d probably know more about that than I would.
I am less sanguine about it for other fields, because I think a big part of journals is prestige. You want articles in journals not just to influence the conversation, but to get publications for your resume, have things other authors can cite without looking dumb, have things that politicians can credibly bring up when making policy, and most important I imagine the journal system interfaces pretty heavily with the grant system. Given all of that, I’m not sure that it’s possible to maintain a separate current of academic discussion outside the journal system if it starts developing a different paradigm and being less than fully commensurable.
I’m also not sure it’s desirable. I’m honored you respect my judgment, but I have an unfair advantage in the sense of I love to write and I have a sense of humor, qualities which are probably not well-correlated with having correct opinions about things. I know a lot of very smart researchers who would be totally incapable of having a blog like this one, and I’m not sure I want to see conversation-setting ability switch from them to people with good verbal skills.
I think part of the reason academic writing is so terrible is to make sure everyone’s writing is terrible and therefore prevent good writers from having an insurmountable advantage. After seeing how much effect on conversations I can have even when I don’t know what I’m talking about, solely because my verbal skills are better than some other people’s, I appreciate the desire to keep that possibility bottled up.
Math and economics are both sort of routing around the journal process these days. In math (my field), you write an article and post it on the Arxiv. And that’s when people care about it and start citing it. And giving you feedback. Eventually you want to get it in a journal to collect prestige/promotion points, but the “having the paper on the arxiv/your website” is the point at which it’s published and the world starts engaging in it.
There are some interesting stronger things going on. People are working on developing what’s called an “arxiv overlay” journal, where the publishing all happens through the arxiv and the journal just gives it a stamp of “this has been reviewed, and also you can tell your tenure committee that we liked it.” There’s also weirder stuff like the Polymath Project, which is an attempt to do freely collaborative math research in blog comments threads, and has published at least a couple papers (with something like a couple hundred credited authors).
Economics I know less well, but Krugman has written about the Facebooking of Economics where for the past thirty years real econ research has happened mostly in seminars and preprints–he comments that by the time he published his famous paper in a journal, people had been citing it for years–and these days is moving more online.
I can’t reply below, so:
“I’m also not sure it’s desirable. I’m honored you respect my judgment, but I have an unfair advantage in the sense of I love to write and I have a sense of humor, qualities which are probably not well-correlated with having correct opinions about things. ”
No. Sense of humor has nothing to do with why you’re being respected. Your intelligence, honesty, open mind and courage to approach politically charged subjects, clear from your work, is an extremely rare and valuable combination in public writings. Thank you for doing that, I hope it won’t hurt you down the road.
That’s a great idea. To help Scott do that, here’s a guide: “How to Publish a Scientific Comment in 123 Easy Steps” http://frog.gatech.edu/Pubs/How-to-Publish-a-Scientific-Comment-in-123-Easy-Steps.pdf
(I find this particular sad/hilarious because last week I ran into a preprint of a blackmarket related paper which is incredibly wrong and the author currently is ignoring my emails, and so…)
So here’s something that jumps out at me in this graph:
Some subjects are a bit above the curve and some are way below the curve.
If we take the X axis to indicate “how mathy do you have to be to enter this field?” then we still have a lot to explain wrt the discrepancy between {CS, engineering, physics} and {chemistry, economics, math}.
(The other data that seems pertinent here is the incredible increase in the proportion of women in the lab sciences over the past 30 years coinciding with a decrease in the proportion of women in computer science … curiously also coinciding with the lab sciences becoming more computational. Some people will probably say, “Oh, the lab sciences are more PC than computer science is.” Or “Computer science is more competitive because of the tech boom.” I’m not sure how to distinguish these from “people in the lab sciences made a big effort to fix their discrimination problems, and people in CS haven’t made as much effort.”)
Sure! Just assume what must be proven, and everything falls into place!
Any statistical disparity which produces more men in a field = prima facie discrimination!
Any statistical disparity which produces more women in a field = Men’s lack of intelligence/emotional connectedness/interest/etc.etc.etc.
Garbage collectors are also disproportionately male. Shall we examine the vast patriarchal conspiracy that keeps women out?
Ummm…. there HAVE been lawsuits against city governments for discriminating against women wanting to work as garbage collectors. This was even parodied on that Parks and Recreation TV show.
Please don’t leave comments like this. You’re mocking something that isn’t present in this comment thread.
It isn’t necessary, because that thought isn’t here.
It’s contains truth, in that what you’re mocking exists, but not very much truth, because it doesn’t help anyone who reads it obtain a more accurate view of the world.
And it isn’t kind. Irrelevant mockery acts as an intellectual gang sign, and calling extra attention to the worst members of a group can be the first stage in constructing a superweapon. Even if you would never attempt that, coming close to it still forces vulnerable people to see to their defences.
Yes, when I say “I’m not sure how to distinguish between X, Y, and Z”, where X, Y, and Z are contrary candidate explanations of a piece of evidence, I obviously mean “Z is clearly true and only evil jerks would doubt it.”
Obviously.
Did people in the lab sciences in fact make a big effort to fix their discrimination problem? If so, is there any consensus on which measures were most effective?
Honest curious question here, from a CS guy curious to see what my field can learn from the experiences of other fields.
I don’t know either. A good first step would be to find a decent measure of discrimination – one that identifies and quantifies concrete elements of discrimination, rather than taking some difference in outcome, maybe controlling for some relevant variable or other, and then declaring that any residual must be due to discrimination.
As more fields have become more computational, the career paths of the CS degree has narrowed. With a CS degree, one can work in “tech”. With a degree in some other field, where you’ve done some programming and lots of computational work, you’re excluded from 10% of the jobs in ” tech “, but have access to jobs in other fields. Jobs which actually have rational management and don’t consume your entire life as a general working condition. Jobs which don’t have tournament pay scales, but which still pay well. So while there are lots of jobs in “tech “, there are more options outside it.
Yes, these two things are probably correlated. My guess is the old comp sci female numbers would have fallen nicely into the math/chemistry/econ cluster, and the new comp sci numbers fall into, well, the cluster they fall into.
It’s interesting that this corresponds to comp sci becoming an important practical industry in the same way engineering is, although I’m not really sure exactly what to make of that.
My guess for why CS GRE scores are anomalously low is that many people in CS take the GRE because they want to get a master’s degree and become software engineers, while in most other disciplines people only take the GRE if they want to do research.
That would predict that CS GRE scores are low. Which is what the paper says. But it is the paper’s bizarre composite that is low, not what anyone paying attention would label as a “GRE score.”
The paper’s “GRE score” is really a verbal score. CS has a math GRE 1 point higher than chemistry, but verbal 4 points lower and writing 0.5 lower (which is huge). So what you really need to explain is why CS is so skewed towards math, not why it is “low.”
Proportion of applicants whose native language is not English would be the first thing I’d look at.
Glad to see that you so thoroughly destroyed that stupid study so that it’s
Debunked And Well-Refuted
On a more serious note, it’s quite dismal that such bad science still gets published and possibly even acted upon…
I hope you are not under some misguided impression that this is the process by which people actually choose what discipline to go into. None of my college chemist friends (who had, ya know, spent four years majoring in chemistry) only chose to attend grad school for chemistry because their GRE scores weren’t good enough to go into economics.
Well, the problem is, if I use that methdology, I get that every single major is either male-dominated (if it requires high math scores) or gender-neutral (if it doesn’t). We need some extra assumption to explain why the low-math-score majors are so heavily female-dominated, and taking the men out of the pool seems to be the best bet.
People who are better able to visualize complex math problems can tell me if I’m missing something.
Could it be that young men who are mathematically gifted are steered towards those fields? “Yes, you could be a psychologist, but your talents are for tech! Think how much you could achieve in that field! Therapists are a dime a dozen but really competent engineers are rare as hen’s teeth!”
Like Gbdub above who says “I could have done well in English, history, law, or psychology” but went into engineering because it interested him. I can see young men who have options like this being steered towards the hard sciences in a way that young women may not be?
To the extent that I was “steered” it would have had to be early and subtle. I have been interested in airplanes and rockets for as long as I temember. I’ve always been “tech inclined” – handy with computers and hardware. And this is pretty typical among my peers – the Dilbert “knack” thing actually isn’t far off. If anything, that’s a more pervasive myth in engineering than genius , the myth that you need to have a real passion for the field to be successful.
So I think I came upon engineering pretty organically, and that seems pretty typical. Maybe women are actively being steered away? Possibly, though to be honest the most discouraging voices are from those outside the field criticizing it for being sexist (my female peers were not impressed with the comet shirt fiasco).
Actually that may be the biggest difference between men and women in my field – almost all of my male peers have a “nerdy” or “techy” hobby. RC planes, astronomy, model rockets, brewing, tinkering with Arduinos, etc. The women seem not to have similar extracurricular interest at such high rates (though still a lot higher rate than the general female population). Could be reflective of lower intrinsic interest? Maybe the women are more likely to be people who showed an aptitude and were steered to good jobs in engineering rather than those with an organic interest? I don’t think organic interest makes you better at the day to day work that most engineers do, but it probably makes you more likely to end up in the field in the first place.
You spend a lot of rhetoric on Mathematics because it is highest on the GRE scale, so to be charitable you should probably also spend a little energy discussing the subjects that are highest on Leslie et al.’s “Ability Beliefs” scale.
The subject that is perceived to require the most genius is far and away philosophy, which doesn’t seem overly mathematical yet has relatively few women. Also very high on the perceived genius scale is music composition, which is <20% female.
You somewhat hint that these subjects require high mathematics ability in your response to the first objection, but I find this surprising. Is there evidence of math GRE scores predicting success down the road in music composition?
It's probably worth at least discussing on a case by case basis some examples which exist outside the STEM universe.
You could tell a story about how math scores are a proxy for ability to think through certain kinds of complex logical arguments, and philosophy demands that same ability in a variant expression. And music composition involves certain sorts of puzzle-solving that are similar to the constraint satisfaction problems you find in math (e.g. species counterpoint exercises). And there is an anecdotally known correlation between mathematical ability and musical ability among my extremely representative self-selected tribe of musically inclined math/CS folks. Also, Douglas Hofstadter. 🙂
But yeah, this is all a stretch, and very probably there is something different going on.
For what it’s worth, the quantitative GRE scores of people going to grad school in philosophy are the highest in the humanities–google philosophy and GRE and you’ll find lots of philosophy department webpages talking about the performance of philosophy majors on the GRE. While philosophy is still an outlier in the “perceived genius scale”, it might not be as much of one as you might think.
I have one anecdote to add to your data. When I was at Caltech (in the 90s) I had a conversation with one of the students on the acceptance committee. They shared that the committee had run regressions on various acceptance metrics and students subsequent performance (grades, dropout, etc.). To lowest order the only score that was relevant was the SAT II math score. If you were below a cutoff number (700 or 750, can’t recall exactly) your chances of being successful plummeted. Everyone on the committee was advised that if they wanted to admit someone who failed this criteria they were taking a grave risk, and that it would likely not turn out well for the student.
They admitted some people in this category, I knew one. I saw many people struggle and drop out at Caltech due to drugs, maturity, work ethic, broader interests and other causes. This person (male) was the saddest, he tried very hard, constantly trying to “catch up”, and always falling further behind. He left before freshman year ended.
I’d say from this that Caltech (a reasonable example of STEM selection) arrived at exactly the type of cutoff you describe above for a high stakes math test score from a consideration of helping students be successful and reducing their likely misery. Whether this lead to sexist results or not, this was the best way an admissions committee full of highly intelligent folks could come up with to achieve this goal.
This fact, along with the data you present above, leaves me with a strong suspicion that all Caltech ever achieved with it’s programs to attract more women to science was to steal them from other STEM focused schools, or STEM departments at other elite institutions.
Note: It may be true, and is even likely, that female performance on high stakes tests is worse due to misogyny. I can’t see how even certainty about this could change the above story. As Scott hint’s above in all likelihood by 11th grade it is too late.
Is Caltech a reasonable example, though? It is a very small institution (~1000 undergrads, ~1200 grad students) compared to other top-tier STEM institutions (about one-fifth the size of MIT). It’s even smaller than some larger universities’ engineering departments.
Oh, and it’s noted for being unusually intense even for a STEM-focused institution, which might have something to do with the genius gap.
Caltech has the highest sAt scores in the nation by a considerable amount. At least of any institution large enough to make common listings. Often it outpaces number2 by 30-70 points.
Caltech is not even representative for a “top STEM school” as the caliber of students is significantly higher.
Quite a lot of this is self-selection. With an SAT I only in the 1300s (out of 1600, not sure what they’re rejiggered it to these days), but other mitigating factors (high SAT II subject tests, your high school being in a flyover state where you have maxed out the meager course offerings available to you, etc) Caltech may well admit you — but many people of this description are scared off by the aggregate scores and don’t even apply.
It’s an outlier of a place but it mirrors a general problem in college admissions, where talented students from poor / disadvantaged backgrounds feel safer applying to state schools, even though they might find better funding opportunities at elite private schools.
Pingback: 1p – Perceived Ability as a Proxy for actual ability explains gender gap – Exploding Ads
Pingback: 1p – Perceived Ability as a Proxy for actual ability explains gender gap – blog.offeryour.com
If majoring in a “math intensive” field raises your Quantitative GRE doesn’t this argument fail. Women might have lower Quant GRe scores because they were discouraged from majoring in mathematical subjects in university. And the Quant GRE does not seem like a good test of intrinsic ability.
Didn’t the study find that the skew is highest in philosophy? How would you explain that difference given that it’s obviously not reliant on math.
Logic?
Where did you get your SAT data from? I see scores by major here, including “precision production,” but I don’t see a sex ratio.
I took the sex ratio from National Center For Educatio Statistics, which conveniently uses the exact same bins as the College Board.
Thanks!
Except that you probably meant the 2013 edition. It has 24% of Precision Production female, matching your spreadsheet, while the previous year that you just linked to was 49%.
Just have to say that reading this post is really meta for me. I’m a fairly mathematically adept woman who’s just beginning to study CS, and I could feel my self-confidence shifting slightly back and forth as I read the comments. Great post, though.
“I could feel my self-confidence shifting slightly back and forth as I read the comments”
If you’re an individual considering yourself, you already have a lot of information about your own ability (grades, test scores, independent accomplishments). Knowing stuff about small average gender differences shouldn’t tell you much more than you already know. I trust you to self-assess accurately when you say you’re a “fairly mathematically adept woman” (if anything I would guess that you’re underestimating your abilities, ’cause that’s what women tend to do).
Let’s say we have a man and a woman who have the same math SAT score, both get the same GPA in the same CS classes, etc. Who is better off? If anything, I’d say the woman is better off… data like Scott’s suggests that she is actually underperforming relative to her genetic potential, so she has greater odds of having super smart kids. Also if both are heterosexual, her dating pool of people cognitively similar to her is much better.
Whatever your ability level is, being a confident, curious learner is always the right approach. Thinking about whether you’re on the wrong career track is fine and valuable, but there’s no need to concern yourself with that when you’re actually doing problem sets, it’ll just hold you back. Your ability to give it your all is one of the few things you do have control over, regardless of innate ability, and doing your best is helpful regardless of what ability level you’re at. So, do your best! And if you’re going to worry about whether you’re on the wrong career track, do it “offline” when you’re not actually learning or doing problems.
How did your self-confidence shift? If it shifted downward, I think that would be a misunderstanding of these results.
Remember, the percent of female grad students and successful female programmers is exactly the same as the percent of women who take the AP Computer Science test in high school. By choosing to study the subject you’ve already passed your filter and entered into the elite ranks of people who have a pretty good chance of succeeding in Comp Sci.
Yes, but this is just a bizarrely lucky coincidence because one group (AP high school students) consists almost entirely of Americans and the other group includes a large proportion of non-American citizens.
What’s misleading is the horrendously shoddy job by Leslie et al and journalists in the past weak in the first place to not notice or emphasize this aspect enough.
Even if it gets the results one expects at some point a toy model that defies common sense does have to be abandoned, that everything is cleanly based on standardized test scores for the entire graduate school selection and admission process. Everyone knows that foreign student university admissions are not decided by such neat criteria. And of course that foreign students are hardly exposed to the exact same “cultural” background that is even supposed to produce the gender gap in the first place!
Telling you that women are on average shorter than men shouldn’t cause you to lower your estimate of your height. The same applies with variance and IQ.
Wrong.
Aptitude measurement is not as accurate as height so group membership should be taken into account.
If she had an imperfect measurement of her height, the average height of women would be relevant for making the estimate of her true height more accurate.
A rational agent should and will discriminate partly based on group membership. The fact that this hurts a lot of peoples feelings does not make it any less true.
1. The relevant comparison is not the a) variance of aptitude measurement compared to b) the variance of height measurement, it’s the a) variance of aptitude measurement compared to the c) variance of aptitude among members of the group. Even if a) is much larger than b), as long as it is much smaller than c), group membership is still a negligible factor.
2. This type of analysis assumes independence. Even if women have less mathematical ability (as a distribution) compared to men, if aptitude measurement is also sufficiently biased against women, taking membership in “women” into account should actually increase the estimation of mathematical ability. Conversely, even if women have equal mathematical ability compared to men, if aptitude measurement is biased in favor of women, taking membership in “women” into account should decrease the estimation of mathematical ability. I will not argue one way or another on the object-level independence; I’m just pointing out that independence or lack thereof is something one must take into account.
I may be missing something, but aren’t you assuming that the existing actual ability distribution in the various fields is the same as the required actual ability distribution?
Hypothetically, if everybody believes that you have to be a natural genius in order to be a competent widgitizer, wouldn’t the statistics on ability amongst professional widgetizers reflect that, regardless of whether it is actually true? Firstly because only those who think they are geniuses will try to take it up as a career, and secondly because widgetizer companies will only hire people they think are geniuses.
(OTOH, I suppose in a way the perception of required ability is a self-fulfilling prophecy; perhaps a person of average ability could be a perfectly competent widgetizer in principle, but I would expect that he or she would still be outperformed by all of those geniuses, and therefore much less likely to be successful. So it depends on what exactly you mean by “required”.)
It looks like women are under-represented in Computer Science according to the GRE scores. OTOH, that’s relatively recent. (The percentage of women majoring in CS is half of what it was three decades ago.) Something is suppressing it and that something has nothing to do with the “Patriarchy.”
What do you think it is, then?
I can think of several possibilities.
The efforts to recruit women into academic fields might have worked to redistribute women from some fields into others.
The myth that CS people are prejudiced against women may have discouraged women from entering CS.
There are other possibilities. Whatever it is, it is working more strongly now than a generation ago.
For a measure resistant to selection bias, we really want to use ether a state or national standardized test – I think the NAEP might be a good choice, but you could also find e.g. Oregon high school math test data or something.
Of course, it seems to show a similar pattern.
Also, I’m not sure that this reflects grad school admissions at all. To first order, I think someone who wants to go to grad school will do so, their admissions just determine where they go. And so the proportion of women in a field doesn’t indicate anything about admissions, but rather about applications.
Again, there are fewer women in STEM all the way through the pipeline, starting at least in senior year of high school – math PhD programs are certainly not admitting a dramatically smaller proportion of women applicants than men! This business about “you must be this smart to get in” is therefore an explanation for something that is non-existent!
Scott,
If only one could do an experiment to determine whether it’s nature or nurture that is responsible for the lower numbers of women in STEM. Say, magically change the culture to the one where girls and women are not automatically considered less technically or scientifically inclined, where the STEM fields do not have the nerdy stigma, and where arts, commerce business and science are all equally respected? Or where a career in academia does not mean delaying having children until your 30s while still struggling to keep up with your male coworkers, competing for the same tenure? And then let this social experiment run for say, oh, 50 years or so?
Guess what. Remember your post lamenting all the Russian crazy meds which, despite likely being effective, attract zero attention in the West? Same story here.
I grew up in the Soviet Union in the 1970s, at the time of “peak communism”, before leaving for greener (literally) pastures (figuratively) much later. There was plenty of casual sexism, and women (and men) were expected to marry in their early 20s, if not before, then have children right away. Women had to be as cautious as in the West when walking alone at night, and cat calls, ass grabs and unwanted sexual advances were not uncommon. Girls played with dolls and boys played with Lego (an awful Russian version of it, not snapping together well, and pieces often breaking apart), as well as soldiers and trucks.
But one thing virtually did not exist, to the best of my recollection, though have no stats handy. No one thought that women are less capable at STEM. Ever since Lenin declared gender equality, among other equalities, back in 1917, women had just as much acceptance in engineering and academia as men. My middle school math teacher was a female (she was very good) so was my physics teacher (she sucked beyond belief, but then I often had lousy male teachers, as well). Our math club had roughly equal numbers of boys and girls. Yeah, I was a nerdy kid. Never got any grief because of that, though plenty because of my poor social skills. My less awkward math-loving friends had few issues. There were no “jocks” that I recall, though plenty of assholes and bullies, but the latter could be just as good at math and science as the bullied. Doing well in school was never a negative. Science was not considered the domain of eggheads, it was just one of the things people did for a living.
Women were as expected to go into Medicine, Engineering and Science as into any other occupations. A few examples. My mother designed ship engines for a living. My grandmother was responsible for air and water quality in an area with probably half a million population. My wife’s cousin got her PhD in under Kolmogorov himself, wrote several influential papers and taught math for decades, first in the Soviet Union, then in the US. My aunt was a computer programmer and is doing very well off, having retired by now. Yet she was considered the “stupid” sister by her parents, compared to my mom who was the “smart” one. In my very STEMish university department there were as many female students as male.
The child benefits were such that American women can only dream of. You get paid maternity leave a month or so before your due date, with your job held for you for six months or so, and held for you for up to three years, if I recall correctly. You automatically get a bit more money when you have children. Daycare/kindergarten was free, or almost free. There was no tenure. That is, you don’t get fired once you are hired, unless you do something criminal. What with being employed by the government and all. There were plenty of downsides to that, but competing for a permanent position was not one. Of course, there was as much politics as in any research institution or a university department. Promotions were few and far between, since almost no one ever left, except to retire, or feet first. Well, I’m stretching it a bit, there were occasional layoffs, just like everywhere else. But rarely any individual firings.
So, the social experiment a feminist can only dream of undertaking had been run for 70 years, with a break to fight a war or two. Or three, but who’s counting. Similar social “experiments” had run in most other countries of the former Eastern Bloc. A nearly perfect control. Of course, then it all came crashing down. But not quite all. The egalitarian attitudes toward STEM and women in STEM did not change, only the economic conditions.
So, given all this, what do you think the result of this experiment was? Feel free to guess or look it up, or just recall what you know. I’ll reply with what I remember, once/if you comment.
I know women were very overrepresented in medicine. I would predict that women would have high representations in other fields as well, but not at the highest (Nobel-winning?) level.
All my family doctors were women. Only a few out of a number of the specialists I saw were female, however.
In my university, despite there being about 50% or so female students, and overall more of them completing their computer degree than male, there were none in the top 5 of my graduating stream of 100 or so. Most of my classmates of both genders (there were not any other genders back then) in our high school for nerds, the same one that one Grigori Perelman went to, majored in Math, Physics, Chemistry, Biology or Comp Sci from the top Russian schools. About half of the guys went on to get a postgraduate degree, and only one or two women.
Sure looks to me like they got shortchanged by an unfairly narrow Bell curve, though maybe there are more politically correct explanations. Maybe they cared more about their family than their career, or something.
When the times turned sour in the 1990s, nearly all of the girls left academia and did what they had to to get by, mostly marketing, accounting, real estate or web design. Some managed to leave the country before Yeltsin hit the fan. They did pretty well in engineering and programming, and I know exactly one who went on to do a postdoc, vs maybe a dozen or so guys, who ended up having a secure research position on Russia, or a tenured position in the US.
None of my classmates of any gender got anywhere close to the Nobel-level, or even became somewhat famous. Well, except for Perelman, who got as famous as a mathematician can get, but we did not intersect in either high-school or university, due to the difference first in age and later in talent.
In any case, my point is that there was a nearly perfect experiment performed, and most Western sociologists just ignore it. So do bloggers, feminist and not, including one Scott Alexander.
Having similar background, I confirm xrushin’s observations.
I will add that to do a cross-cultural experiment you don’t even have to go back in time.
Today software engineering is dominated by immigrants who come from very different cultural backgrounds.
My casual observation is that among immigrants the ratio of female software engineers is higher than among natives, but still very low.
Another observation is that out of the women who start out as software engineers very few stay on the technical path. For the most part they tend to switch to less technical specializations like project management, administration, or serving as liaisons between Engineering and Business.
Wouldn’t part of the reason for this have been that the army sucked up a lot of the talented men?
There were three years, later two years of military service compulsory for all men. And the army had a lot of prestige: A conscript noted for talent might have had a hard time refusing an army career for a scientific or medical one.
On the contrary, university was a refuge for nerds who wouldn’t fare well in the hazing-happy environment of the army.
Of course, both individual scientists and entire institutes could be used for military needs later.
And the army could keep the smartest guys after shorter educational paths, I suppose.
I believe you have this exactly backwards. Back then (in the 60s..80s, not sure about now), every young man’s life pretty much revolved around the problem of the army; specifically, how to survive it.
If you were even moderately smart, your entire mission in life from middle school to high school was to get into a university, and to stay there for a post-graduate degree, by any means necessary — because doing so would grant you an exemption from the draft.
The penalty for failure was the Soviet Army, where you will most likely be injured, physically and mentally crippled, or killed — not by the enemy, but by the older conscripts or the wardens, sine the entire system was basically run as a concentration camp (and still is, AFAIK).
This could explain the higher proportion of men in Soviet STEM fields (and other post-graduate studies). They literally had their lives on the line, so they were quite highly motivated.
The life of young men in Russia revolves around avoiding the military draft now. In 60s..80s the Soviets were much better at:
1. Hiding all the problems in the army, and maintaining a good reputation for it.
2. Actually funding the army, so at least the soldiers weren’t underfed.
3. Ensuring that your life will be shitty if you avoid the military service, even legally. At very least one should have gone through a short training an an officer according to their undergrad major. Currently, avoiding the draft is only bad for you if you do so by failing psychiatric evaluation (results in the inability to get a driver license, work for the government, and sometimes creates problems with other employers too) or illegally (results at very least in being unable to get a passport and leave the country, and tons of other problems), but otherwise it doesn’t deprive you from immensely useful social benefits. It did back then.
According to Wikipedia, there have been about fourteen Soviet/Soviet-educated scientists who got the Nobel prize. None were women.
So we’re supposed to change our minds based off your anecdotes and perceptions?
“So we’re supposed to change our minds based off your anecdotes and perceptions?”
It is interesting that you perceive this group as having a collective mind and uniformity of opinion.
We’re supposed to be tantalized enough that at least a few of us go off and read more about gender and STEM in communist countries.
I’ve looked at this before, and been impressed with the statistics. It seem the former communist countries have indeed done a proportionately much better job in producing female mathematicians.
If you look at page 1253, table 7 of http://www.ams.org/notices/200810/fea-gallian.pdf , you can see that female recent European immigrants, especially from Eastern Europe, substantially outnumber female white natives, especially non-Jewish ones, among new junior and tenured math faculty at top US universities.
That’s in total, and corresponds to per capita rates many, many times greater (50-100x). That’s very impressive even considering the selectivity of migration. Eastern European countries haven’t eliminated gender gaps (see page 1252), but they have done a much better job in causing mathematically talented women to enter and remain in the field and to develop their skills.
That’s enough to say that the numbers for U.S. native females could be brought up from where they are now, and to reject the view that the status quo simply reflects the distribution of innate abilities and dispositions.
The communist countries were good in quantity of child care. After excellent maternity leave, you’d be sure to get a place to put your two-year-old. So girls’ investments of time and effort into education wouldn’t be threatened so much by the dreaded possibility of becoming a single mom.
(Quality of child care was utterly appalling by our standards, though. That’s why the state could afford it.)
It looks like a big part of it may have been the much greater prominence and pay of STEM (especially E, and M) relative to other occupations in the Soviet Union, so that learning math was the clear choice even if you might have wanted to do other things in a country with a different distribution of rewards.
A much larger share of talented people went into STEM fields in the Soviet Union, while managers were marginalized (or had to be engineers).
http://www.airpower.au.af.mil/airchronicles/aureview/1979/jul-aug/heuer.html
The paradox is that of calling it a paradox. That people align their careers more with their interests, as the pressure to obtain (perceived) necessities weakens, seems perfectly intuitive.
The entirety of the paradox lies in the false assumption that men and women are interchangeable, beyond their primary and secondary sexual characteristics.
The view is usually very male-centric as well. So to reference the study, why would only 18% of physics graduates be women when 32% of women generally should be good enough at math to graduate? The really easy explanation is “getting a degree in Physics and then working in the field is a GIGANTIC PAIN IN THE ASS, and women have better alternative options than men, especially in the most prosperous countries.”
Or people will ask, “what keeps women out of computer programming?” Uh, the same thing which keeps men out of it. It’s boring, hard, tedious, and really, really frustrating.
Hungarian here. In my experience this all was about an elite. Urban, educated parents etc. Gender roles were very much alive in 95% of society. In the lower classes women did not become car mechanics, men did not become nurses. It was only for the _intelligentsia_. Who were a wholly separate class.
One interesting thing. In the last 25 years, in the hyper-mafia-capitalism that came after the collapse, gender roles intensified a lot and really this is something that cannot be blamed on traditionalism: it was entirely new. And I was trying to figure out why.
And my best guess is that money, resources became scarce and laws became not important: hence to get money and status in the new “capitalist” system was not through honest performance but through bribing, cheating, aggression, or at very least bullying and destructively competing.
In the new economy, a woman could do a good performance job as long as only honest work was needed: but honest work was no longer enough. Now, to win a tender, one had to walk up to the customer and shamelessly offer a bribe or threaten them or something. And women were simply not aggressive enough, not crude enough, not brutal enough for this.
So we went back to the old system where men (semi-literally) fought and killed each other for money, bring home the money, and women would get money by attaching themselves to me.
This resulted in men adopting a tough gangster chic, and women adopting a cutesy-childish, sexy-Hello-Kitty, infantilized and whorish outlook. Men: shaved head, women: false nails, that kind of thing.
This really taught me a lot about the biological basis of gender roles. Women can compete as long as they need to be purely productive, when money really _earned_ by doing a good job, when it is really about merits. But once it goes beyond that, when you do not earn, but fight for, loot for money, when doing a good job is not enough, when you must be more aggressive and throw bribes and threats left and right and basically be like a mafioso, when merit is not enough becomes success needs to be grabbed, robbed, looted, then women have no chance and thus their only chance is snatching a succesful mafioso as a partner which means they need to be feminine, childish, submissive and whorish.
So our post-collapse social environment is basically an experiment in recreating the Ancestral Environment we evolved for. In Russia too. Same thing.
Today I see the world as pockets of civilization where inside people compete on merit, and in this, women can compete. Outside, they compete on aggressivity, and there they cannot compete and thus their chance is only snatching a succesful man.
I think women made civilization. It is very hard for women to compete outside civilization.
Iran is pretty horrible in that regard, both for women and men. Women get to take educations, sure, but jobs are another matter. Just some 15% of Iran’s working force are women.
Not that they need jobs, since it’s strictly their husband’s or father’s responsibility to provide for them. Any income they have is basically pocket money, for them to use as they please. That is part of Islamic law in Iran. It’s also the way it used to be in the west, and here as in Iran it’s naturally used to justify wage discrimination.
Iranian women are educated for prestige, not for profit. I consider it little better than slavery. But people in the west shouldn’t assume that luxury-loving Iranian women necessarily feel that way.
Morgolis and Fisher’s Unlocking the Clubhouse talks a bit about how American women switch out from the computer science major at a much higher rate than than international students from, say, India or Malaysia. Their explanation seems to be that the American women worry about whether they “fit into” the percieved nerd culture:
Meanwhile, they write, the South/southeast asian students have a “reference group” (their family or compatriots) which is different from their major, and they have strong reasons for doing well. (E.g. if they don’t pass the course there will be consequences with their visa-sponsoring company, or their parents don’t have a work permit so they need to quickly get a well-paying job to support their family). So they just suck it up and work hard.
To me, it seems like the difference is that the American students are at the higher, self-actualization, level of the Maslow pyramid—for them a college major is not just a way to feed themselves, but a kind of subcultural statement, like being goth or prep…
I don’t think there’s any good evidence for a well-defined hierarchy of needs per Maslow; in fact, I think his hierarchy is antipredictive in a lot of situations. And you might be putting too much emphasis on the immigrant angle; I get the impression that the gender ratios seen in those international students’ countries of origin, where we wouldn’t expect visa sponsorship et al. to matter, are closer to those we see among international students in the US than among American students.
But I do buy the basic idea that a CS degree is culture-marked for American students in a way that it generally isn’t outside the US. It fits well with my theory that Americans think about intelligence and technicality (and rationality!) in ways that entangle them unnecessarily with the nerd culture. And vice versa, of course; this has as much to do with attitudes inside that subculture as stereotypes outside it.
I might offer an explanation. White American women sit at the very top of the “sexual food chain”. All ethnic groups and especially white males rate her higher than any other ethnic group in sexual desirability. Indian and east Asians rate somewhat lower, perhaps quite a lot lower.
Women do not need work to attain their sexual market value. It is a given as a function of youth, attractiveness and overall “fecundity”. Work merely buys her time, occupies her, and provides access to males. A higher level occupation provides her access to a higher level of males. Asian women that work in STEM often have a far lower sexual market value, vis a vis that of white American women. And thus, fewer options.
Note from the comments of the white woman quoted above. It is just “hamster” talk that says she has no intention of compromising her sexual power and sexual capital in any way in order to “fit in” with what she perceived to be males of little sexual value. I worked in tech since 1985. My observation is that the men are perfectly sociable. It is the women that lack the social skills in dealing with the typical tech guy. This woman in the above comment is a perfect example of that. She refuses to budge one iota in compromising to the group identity. And why would she? She has far more social power as a woman than most geek STEM guys ever might possess.
It has been noted, (heck more than noted. It is a seminal tenet of the Manosphere) beta males, especially geeky beta males, men who exhibit very few of the traits that women find attractive, and exhibit quite a few of the traits that actually repulse them in a very visceral manner. Women use the words “creep”, “creepy” when describing these men.
And in the past 15 years or so, more and more of the members of technical staff are Indians, men that severely “creep out” white women and ping those egg protection tendencies. Foreign women are less repulsed by these men, and really by any men than American women are.
For white women in particular, and for American born women in general, it is about “comfort”. One of the deep unstated demands of feminism is “keep those betas away from us.” In high school they are little bit more protected in the “STEM” classes by the rigidity of the social hierarchy and by higher numbers of females in college prep sorts of classes. In college things get a little closer and the “creepy” betas have more anonymity. And at work, well, as one woman said, “a room full of socially awkward men who don’t know how to talk to her.” They know how to talk to her. She responds to it differently and with more disgust than if the man were a high status, attractive male.
So women prefer the comfort of segregation, a woman-safe place where “creepy” beta males do not have access to her. Or if she can get in, a place crammed full of sexy high status males. The cubes of a high tech company filled with low sexual market value males is not that place.
When you use technical terms inappropriately, it doesn’t make your argument more persuasive. It just makes your readers cringe.
Not every ordered list is a fucking “food chain”, OK?
This is a plausible and interesting theory, but this part:
…doesn’t really square with my lived experience. I’m also a professional software developer, although I’m quite a bit younger than you. What are you basing this on, other than the quote from Unlocking the Clubhouse? And, for that matter, what is your argument that the woman is obligated to change to “fit in” to the culture she finds herself in?
Do you have a reference? I thought that most men have a preference for East Asian women, probably due to neotenic facial features. For instance.
Then why are feminists demanding more STEM jobs for women rather than more jobs in alpha-laden fields such as law or medicine, or oil well drilling?
I’m under the impression that women tend to benefit from environments full of submissive beta males, due to the “white knight” and “friendzone” dynamics. That’s why it was so easy for SJWs to invade all geek spaces.
Alpha males, on the other hand, tend not to submit to women, they aggressively compete with them in a professional setting.
Leaving aside whether any of the conclusions follow if we grant it, I don’t think the contention that “white American women sit at the very top of the “sexual food chain” is even accurate in the first place. Asian women seem to experience more sexual attention from men of other races on average, anecdotally and according to internet dating statistics. But Asian women are more represented in STEM fields than white women.
Scott, what an amazing and absolutely brilliant post! I may add this to my HBD Fundamentals page in fact.
Now that said, why did you add this paragraph?
Well, to be accurate, not many of those supposed “environmental determinants” hold up to scrutiny – or, at the very least, aren’t too relevant to most people in today’s world.
There’s no evidence that exposure to “intellectual stimulation” matters much nor is there evidence that there exists “crucial developmental windows.” Even the effect of malnutrition is questionable. See Greg Cochran on it:
The Great IQ Depression | West Hunter
Even the stories of the infamous Romanian orphanages may be muddled:
http://twitter.com/JayMan471/status/552940525230522370
Overall, the effect of any parental treatment contribution to adult intelligence appears to be nil. For if it wasn’t, it’d show up in the shared environment term on IQ in behavioral genetic studies, which, as we know, it doesn’t.
Now, if you’re saying (as Cochran did) you don’t want you lock your kids up in a dark room all their childhood, sure. But since the overwhelming majority of children in the Western world aren’t, this is a non-issue, practically.
Anyway, those quibbles aside, great work, again! You busted a myth that (still, it seems) sorely needed busting.
“Now that said, why did you add this paragraph?”
Several reasons:
1. To cover my ass, obviously.
2. A friend whose opinion I respect urged me to do so, for both PR reasons (as above), and for truth-related reasons (as below)
3. Environmental determinants do so affect IQ. See for example my Biodeterminists’ Guide To Parenting. I have a feeling you will dislike it intensely, but the ensuing debate should be interesting.
4. I’m impressed by the arguments that the Flynn Effect is sort of cheating. That is, it seems to be a sort of extra-IQ tacked on to real-IQ that doesn’t have all of the biological correlates that real-IQ does. I find the argument that the Flynn Effect is produced by greater education and familiarity with reasoning pretty convincing, though not so much so that you couldn’t change my mind. I would expect greater education and familiarity with reasoning to produce a Flynn-like effect on SATs and GREs as well.
5. Evidence from eg Ireland, which used to have very low IQ but which has since mostly normalized, seemingly in accord with better nutrition and more reasoning-based society. Same with Irish immigrants to US.
6. IQ 70-80% genetic suggests 30-20% something else. Although some speculation that this may be vagaries of embryogenesis, also leaves a lot of room for other nonshared environmental factors.
7. Some evidence of developmental windows, eg with language – I don’t have a strong opinion on whether babies really have an easier time learning languages than adults, but I have seen studies showing that they have better ability to learn phonemes – that is, your phoneme-detection is learned by age 3 and if you want to learn new phonemes after that it’s an uphill battle. See also that experiment with the kittens raised in an environment without vertical lines who never developed the ability to see vertical lines even when released from that environment.
8. GREs correlate 0.7 with IQ, which means there’s a lot of room for non-IQ related factors to affect them. Plausibly some of this is amount of education. I don’t know what the rest is.
9. I find Mertz somewhat convincing, or at least I cannot immediately dismiss her in the same way as much of the rest of her field. I would be interested in hearing your opinions on her work.
Thank you again for the compliments, and I’m interested to hear what you have to say about the above as most of them are areas where my opinions are still forming.
You should have a strong opinion! For every aspect of language except the one example you gave, adults are faster at learning second languages than children. See here or public.
Evidence from eg Ireland, which used to have very low IQ but which has since mostly normalized, seemingly in accord with better nutrition and more reasoning-based society. Same with Irish immigrants to US.
Ah, ’twas all the fault of the p’taties, sor. When we went out foreign and got our first taste of Real Food, sure we were fair bursting with the brains, so we were! 🙂
We have a reasoning based society? That’s news to me!
Or maybe things like my parents having to leave school at fourteen with very patchy education in order to work not happening so much over the recent decades might have something to do with it? My mother was ill-educated, but not stupid; when she went to England at seventeen and got a job in a kosher jam and fruit-processing factory, she was eventually offered a job in the laboratory to take her off the factory floor and train her in (she turned it down because she had no confidence in her ability to write and spell well, due to aforesaid patchy education).
If you had given my mother a standard written IQ test, I think she’d have done poorly on it. I also think it wouldn’t have been a reflection of her true IQ.
“Or maybe things like my parents having to leave school at fourteen with very patchy education in order to work not happening so much over the recent decades might have something to do with it? My mother was ill-educated, but not stupid; when she went to England at seventeen and got a job in a kosher jam and fruit-processing factory, she was eventually offered a job in the laboratory to take her off the factory floor and train her in (she turned it down because she had no confidence in her ability to write and spell well, due to aforesaid patchy education).
If you had given my mother a standard written IQ test, I think she’d have done poorly on it. I also think it wouldn’t have been a reflection of her true IQ.”
This is exactly what I mean by “reasoning based society”. A society that has a lot of education and exposes its citizens to reasoning problems frequently (in part by having them do white-collar work, or by having complicated-to-use technology, et cetera)
If you cover your ass, that’s fine, even Galileo recanted, but it defeats the purpose to immediately admit that’s what you’re doing.
Not necessarily. Scott is not literally before the High Heresy Court of Political Correctness right now (yet. growth mindset). He’s in a blog comments section that is unlikely to be read by most outsiders visiting this page. Plus, it is plausibly a joke, even with my having said so 😛
So here are my thoughts:
The first thing is a task-simplifier: write-off anything that comes from a straight correlational study as being uninformative, and generally useless. The bulk of the studies discussed there are of that kind, hence don’t really qualify as good evidence.
The second simplifier is ignore small randomized controlled trials. I say show me the funnel plot. 🙂
I understand the PR bit. I’m glad you admit that part. 🙂 People don’t want to hear the awful truth, so some need to be cavalier about it (not me, though).
As for those environmental determinants, virtually all the evidence given there falls under the correlational umbrella. I’m even starting to question the supposedly “ironclad” detriments to IQ like lead exposure. See this meta-analysis by Flynn et al. All those things that supposedly negatively impact IQ are all “hollow” with respect to the g factor.
The above meta analysis (and this one by te Nijenhuis & van der Flier) demonstrate that the Flynn is effect is “hollow.” People aren’t actually any smarter, at least not by the g factor. This points to education (testing familiarity) as the source of the Flynn effect. Some argue that there is some real practical increase from these hollow gains, but I think it looks doubtful.
As for the Ireland bit, HBD Chick went up and down that matter.
I would posit that the true heritability of the g factor is in the 0.8-0.9 range. That leaves 0.1-0.2 of the variance to the “environment” – the “unshared environment” specifically. Evidence is piling up that this is indeed mostly just the “vagaries of embryogenesis” (i.e., developmental noise). See my post Environmental Hereditarianism – the susceptibility of which appears to be under genetic control (more research on that is needed. It may be an anathema to ask what the heritability of “unshared environment” actually is, but it seems like something worth investigating. (One way to do it is to look at an extended twin design: are families where MZ twins are more similar more similar to each other overall, even for distant relatives? This may have very low power to detect such an effect, but it’s probably worth doing.)
As for developmental windows, there appears to be some critical periods for certain forms of brain development (see here about a man who regained sight only in late life). But the key thing here, to the extent that this stimulation is important virtually everyone in the developed world gets it. If one is looking to say boost the IQ of your children, this wouldn’t be where to look.
As for the GRE correlation, that’s not too far off from how well different IQ tests correlate with each other.
Mertz’s work would be a post of its own. 🙂
The link formatting in “See this meta-analysis by Flynn et al.” is broken.
Sorry about that. Here it is:
The g beyond Spearman’s g: Flynn’s paradoxes resolved using four exploratory meta-analyses
At some point we need to discuss the uses of correlation, but this probably isn’t it.
If Mertz’s work is a post of its own, it is a post I would love to see you make.
That has actually been tried and it didn’t seem to cause any permanent damage. From The g Factor by Arthur Jensen:
Of course, with N=1 you cannot generalize much.
What.
>No. I used gender differences in the GRE scores to predict what scores we would expect each major to have if score differences came solely from differences in gender balance. This predicted less than a fifth of the variation. For example, the GRE Quantitative score difference between the average test-taker and the average Physics graduate student was 9 points, but if this were solely because of differential gender balance plus the male test advantage we would predict a difference of only 1.5 points. The effect on SAT scores is similarly underwhelming.
I don’t understand this part. Can someone explain it in simpler language?
On average, men are taller than women. Take two disciplines A and B, and and say that A is 60% men, B is 60% women. Let’s suppose that this disbalance is for reasons that have nothing to do with height. It’s other factors that determine who is able to enter A or B and succeed there, and why A ends up with more men while B ends up with more women. In that case A would still have higher average height than B, just due to the fact that men are taller on average. We can easily estimate just how taller on average A members will be, due to higher probability of being men compared to B.
Maybe test scores are like height: A and B don’t really require different test scores, it just so happens that for other reasons A is more men, B is more women, and since men have higher scores, A ends up with higher scores. We could estimate how higher just by using A and B’s gender makeup and average test scores per gender. But when we run the numbers, the difference between A and B comes out much smaller than it actually is in real data about A and B’s test scores, which we also have.
So it looks like there’s something about A that attracts or requires people with higher scores (which are more often men) rather than men (which more often have higher scores). Well, it could be both; but it seems that the former is much more important than the latter in terms of explaining test score discrepancies.
The study has a competing hypothesis that women prefer empathising to systemising. The fields mentioned are systemising. A similar hypothesis is that women with an interest in rational disciplines prefer combining social and scientific fields, and the fields mentioned do not do this. So rational women go into applied science or interdisciplinary fields (Geography, Anthropology).
In the UK, 1.4% of girls and 5.4% of boys study A level Physics. The most common reason given by girls for not choosing Physics is that it lacks social context. Of the pupils who take A level Physics, 24% of girls and 8% of boys go on to undergraduate courses in medicine and dentistry.
Increasing the number of female engineers or physicists seems to create the problem of poaching women from medicine and from fields like Anthropolgy. I consider it more socially valuable for women as a group for there to be female doctors than engineers. I also don’t want to see people with knowledge of the natural sciences drain out of fields like Anthropology and Geography, increasing the dominance of non rational approaches.
(I am being somewhat vague with ‘scientific.’ Maths and the materially real)
It would seem to me that it is hard to declare anyone a genius in a field that combine
General observation on the nature vs. nurture thing: my impression is that red tribe members are more willing to accept the idea of innate differences in abilities among races and the sexes, whereas blue tribe members tend to emphasize nurture. Yet red tribe members seem also more open to the idea of some cultures being inherently “better” than others.
Yet it seems to me that if you believe strongly in the power of nurture, then that also suggests that some cultures ARE better than others, since the “culture” of a group exerts a big effect on what kind of “nurture” its children will be exposed to, no?
I can make the position I’m ascribing to Red Tribe coherent by positing that groups with higher innate abilities develop “better” cultures (where “better” is defined as producing better outcomes in terms of things like crime, income, health, etc.) which then capitalize on innate advantages. I’m not sure how one might square the views I’m ascribing to Blue Tribe, assuming it’s possible. Is it that nurture matters, but nurture is all about money and pre-existing societal institutions and not at all about group attitudes toward work, education, family, etc.?
You assume that Blue Tribers believe that all cultures are equally good. Some do, but it’s mostly backlash against the very psychologically tempting and previously mainstream view that our culture is the best, and everybody else are dirty savages who should be reeducated for their own good.
To avoid this “dirty savage bias”, Blue Tribers prefer to leave the harshest cultural criticism up to the members of the culture in question, and try to phrase their own criticism in charitable and compassionate terms. There are some exceptions for cultural practices considered especially harmful to individuals, such as FGM or capital punishment for “immoral” consensual sex.
As for different cultures within the same society, labelling the best attitudes to work, education etc. “white culture” is probably not helpful to individuals who would like to adopt these attitudes while not being white.
To avoid this “dirty savage bias”, Blue Tribers prefer to leave the harshest cultural criticism up to the members of the culture in question, and try to phrase their own criticism in charitable and compassionate terms
Manifestly false when the culture in question is Red Tribe America.
Looking further afield, the Dunning-Kruger effect applies to cultures as well as individuals; the ones most in need of criticism are the ones least likely to engage in self-criticism.
Red Tribe is a complicated case because Blue Tribe perceives them as a major power in cultural discourse, a power which will bring back the old days of smugly crushing the weak if the Blue Tribe fails to effectively oppose it.
Well, cultures don’t have minds, so that’s a bit of a stretch. The idea is that individuals will criticize the culture, not that the culture itself will engage in self-criticism somehow.
Yes, I understand that the idea is for individuals to criticize their cultures. The problem is that extent to which a culture needs criticism is I believe strongly correlated with the extent to which that culture punishes its own members for offering such criticism. Where criticism is really needed, it can only come from the outside.
With Blue Tribe itself as a prime example.
That’s not complicated. It’s a straight-forward case of dropping the principle when inconvenient.
One also notes that at least one culture they object to criticism of is trying to impose the strong ruling over the weak by force, so by logic they should criticize it too.
Delete for double post.
I didn’t call this “white culture,” I only cited the example of a white, educated family to contrast with a minority raised in a minority culture. These traits (emphasis on hard work and education) are not even particularly associated with white people in the general culture. They are more associated with Asians, Indians, and the Jewish subset of white people.
Oh, I thought you were alluding to “Protestant work ethic”, not “tiger mom”. I’m not aware of wide-spread efforts to implement Jewish/Asian parenting practices in Red Tribe families, either.
It’s very easy (and tempting) for that attitude to become one of blame. These people are the natural underclass and it’s their own fault that they’re mired in poverty! Whereas me and mine got ours by natural talent and hard work, it’s nothing to do with the classism and racism and sexism baked into the society! I see that at my job, where my office manager often says “My God, we had no idea how lucky we were with the parents and raising we got”. Not that we are all products of well-off college educated middle and upper-middle class families, but that we had parents who were present, involved, not neglectful and not abusive.
I’m betwixt and between; for the Blue side, I’d say “You have to insist that people take responsibility. You have to acknowledge that there are scammers and cheats out there. After you make all the allowances you can, there are some people who are naturally less able and some people who are plain downright criminals and it’s not all or even majorly the fault of Society”.
For the Red side, I’d say “Some people are naturally less able. That does not mean they get abandoned in a Social Darwinist ‘weakest go to the wall’ struggle. And there are societal and cultural disadvantages, where early intervention for better education, more support for the families, better and more readily available health care, mental health support, etc. does make a big difference. You don’t know if the next Washington Carver, Alexander Fleming, Amadeus Mozart or Michaelangelo is out there but because he or she is living with a single parent and going to a school that’s really a holding cage and there is no employment opportunity that they can see, we’ll never know because they’ll end up sucked into a gang and in jail, or dropping out early and ending up having a baby. And blaming bad life choices on people whose choices are restricted to crappy choice A and less crappy but still crappy choice B so we can wash our hands of any responsibility or duty is not on, even if you dress it up as biology and science at work”.
Well, I am a reddish-grey tribe member who grew up in the south, so while I don’t exactly speak for the mainstream of the GOP, I think I have a sense of what many of them (such as my parents) think, and I don’t think any of them think “well, some people are inherently inferior and so deserve to fail or be relegated to crappy jobs forever.” I do think they think some cultural attitudes are inherently more civilized or promoting of success than others, and I’d agree with them there.
If you talk to my parents, for example, what you’ll hear is “black people were hard-working before all those programs designed to ‘help’ poor people came along and encouraged them to be single moms and milk the system. Now they’ll never get ahead because we’re ‘helping’ them too much.”
Now it doesn’t change the fact that when my parents were children it was still Jim Crow, or that their parents or grandparents probably grew up assuming black people were inferior regardless of how hard working or family-oriented the black people around them might have been, but that’s not the attitude of anyone I’ve ever met today. Maybe my grandmother is a Paula Dean type nostalgic for the days of dapper black people in white tuxedos serving fancy food to white people, but I also think she’d be happy to see them more successful than that. It’s just that between the gang members and the tuxedos, she’ll take the tuxedos.
The mainstream of red culture today is not “black people are inferior and so deserve to fail,” it’s “black culture has lost the values of hard work, family, etc. due to blue tribe policies.”
Related note: I think this view may be controversial (even before recent scandals), but I think it was cultural phenomena like “The Cosby Show,” along with personally knowing actual hard-working black people that are responsible for a big part of the reduction in anti-black racism we see today. People may object that “white people only liked Cosby because he made black people seem like white people,” but I think that’s sort of exactly the point. I’m not sure anyone is truly capable of empathizing with people whom they view as fundamentally foreign or incomprehensible.
I think people can empathize with people who speak a different language, eat different food, listen to different music, etc., but I don’t think groups with more fundamentally different values can do so easily, if at all.
I’m not part of the Red Tribe, but I grew up in a place where it had some influence, and I think your analysis of Blue Tribe vs. Red Tribe views of these questions is right on the money. I have never once heard a Red Tribe member say anything like “some people are just naturally more productive than others but the Blue Tribe refuses to acknowledge this”. The only people whom I’ve ever heard say anything like that are (a subset of) the Gray Tribe.
I think that there’s a certain brand of American-style egalitarianism that informs Red Tribe politics, strange as it sounds. The idea is that sure, everybody doesn’t get the same amount of innate qualities, but that ultimately isn’t morally relevant. What is morally relevant is that everyone has the potential to be a hardworking, productive member of society, and anyone who manages to do this should be rewarded, regardless of what circumstances they were born into or how they did in the genetic lottery or whatever. (And economic redistribution is bad because it decouples people’s economic outcomes from what they deserve under this paradigm.) The idea of a natural permanent underclass is abhorrent. See also: Americans taking pride in America’s high degree of social mobility, which of course doesn’t actually exist.
(None of this extends to people in other countries. I’m not totally sure why. Maybe nationalistic parochialism is part of Red Tribe moral intuitions or something?)
This, of course, traces back to the meme we’re all familiar with wherein traits like conscientiousness are treated as having moral significance while traits like raw IQ aren’t. The Gray Tribe has noticed that this is kind of stupid, given that those traits are pretty much analogous in terms of what causes them and what they affect.
(The Blue Tribe doesn’t seem to have noticed this; as far as I can tell their cultural memes are the same as the Red Tribe’s in this respect. They do point out the social mobility hypocrisy, but think that the Red Tribe’s big mistake there is its rejection of economic redistribution and denial of persistent social inequalities along not-morally-relevant lines like race.)
What answer the Gray Tribe comes up with from there is the subject of internal divisions, with neoreactionaries having one answer and left-libertarians having a different (IMHO correct) one.
I think it’s an exaggeration to say that upward mobility in the US does not exist. Though I’ve seen some studies claiming to show it’s lower here than in Canada and Scandinavia (a correlation with redistributionist policies I’m sure blue tribers would be quick to point out, though I notice it doesn’t seem to hold in many other cases), it’s still really high by global and historic standards.
Compare growing up in a poor rural or inner city family in the US to being a rural Indian farmer, or anyone in the middle ages.
The question is, do redistributionist policies, on net, help mobility by providing opportunities for education, etc., or hurt by eliminating incentives, slowing growth, promoting counter-productive values, etc.
Re. not extending compassion to foreigners, though red tribe members seem to be more guilty, I notice it’s actually really prevalent among blue tribe members, too. People in the labor movement, for example, complain a lot about being undercut by foreign competition. Of course, they couch it in terms of the evils of sweatshops, exploitation, etc., but what it boils down to is that they are anti-globalization because people in China and India can and are quite happy to do many things Americans used to do at a fraction of the cost.
This was always particularly weird to me, since so many of the blue tribe arguments are compassion-based, yet the compassion seems to stop at our borders in a strange way. If we were really about helping out humanity and not our ingroup, then all the money now spent on US welfare programs should probably go to providing clean water to the third world. If we’re not all about compassion, then why are we forced to help these particular needy-but-not-super-needy people who happen to share a geographic proximity?
America does have some social mobility; we just don’t have a high degree of it by the standards of high-income countries.
You may have hit on something that I didn’t consider with regards to Blue Tribe parochialism. But I don’t find it surprising or interesting that the labor movement doesn’t like globalization; that’s just good-old-fashioned economic self-interest at work. What I do find interesting is that the well-educated upper-middle-class part of the Blue Tribe holds the same attitudes despite not having any selfish stake in them.
My guess is that compassion-mediated-by-fuzzies plays a much larger role in Blue Tribe moral intuitions than in those of the other tribes. Hence they object to blue-collar Americans (who, it should be noted, are also their political allies) losing their jobs, and they object to foreigners working in sweatshop conditions. But the idea that globalization is ultimately positive for developing countries? Is not exactly a vector for fuzzies, since the immediate outcome is just more sweatshops. The Red Tribe doesn’t seem to care about this, and the Gray Tribe uses either shut-up-and-multiply logic or some entirely different set of moral criteria.
I am a left-libertarian proud member of the Grey tribe. My family is all red tribe. And I agree strongly with Taymon’s post.
The study has a competing hypothesis that women prefer empathising to systemising. The fields mentioned are systemising. A similar hypothesis could be that women with an interest in rational disciplines prefer combining social and scientific fields, and the fields mentioned do not do this. So rational women go into applied science (medicine) or interdisciplinary fields (Geography, Anthropology).
In the UK, 1.4% of girls and 5.4% of boys study A level Physics. The most common reason given by girls for not choosing Physics is that it lacks social context. Of the pupils who take A level Physics, 24% of girls and 8% of boys go on to undergraduate courses in medicine and dentistry.
Increasing the number of female engineers or physicists seems to create the problem of poaching women from medicine and from fields like Anthropolgy. I consider it more socially valuable for women as a group for there to be female doctors than engineers. I also don’t want to see people with knowledge of the natural sciences drain out of fields like Anthropology and Geography, increasing the dominance of non rational approaches.
@Audrey
The study has a competing hypothesis that women prefer empathising to systemising. The fields mentioned are systemising.
In his famous luncheon talk, Summers mentioned a possible factor in high/earlier dropout of women who were professionally employed and doing well in certain high status, high pressure fields. To reach high levels required almost constant time and pressured work, leaving little time or energy to “have a life”; so when they observed these actual working conditions, women wisely dropped out (and some caught on to this while still in school, and switched majors).
Do the empathising career fields run at lower pressure than the systemising ones?
Do the empathising career fields run at lower pressure than the systemising ones?
Have you ever met a social worker?
A close friend of mine was a social worker in the child protection area. Worst job in the world. I don’t know how he even retained his sanity never mind continuing to do his job. And yes, it’s high pressure in the “insane amounts of overtime” sense as well as the “possessing the social skills and insight to manage unimaginably difficult people” sense and the “seeing sights which sear your soul” and “endlessly and futilely battling the hopelessness of the human condition” kind of ways.
That said, I think there may be more of a culture of presenteeism in the STEM fields.
We have a searingly low opinion of social workers in my current job (and I picked that up in my previous job) but a lot of it is not their fault, it’s down to the job situation.
Economic straitened times means reducing public spending. The low-hanging fruit of that for a government trying to get voted in on an austerity platform is “reducing the numbers in the public and civil service”.
Because the general public has the image in its head (due to pop culture and media) of civil servants of all being pencil-pushing, tea-drinking, clock-watching bureaucrats with inflated salaries and cushy pensions all paid for at great expense out of the public purse by the taxpayers’ money, this goes down well.
People forget that teachers, nurses, council workers, and social workers are part of the public services. So when there is a recruitment embargo (no new hiring to replace retirement and natural wastage), overtime bans (no working overtime because this costs too much in pay) and no expansion of already over-burdened services, you get massive burnout, you get people loaded down with new cases and so everyone just gets a cursory examination and no follow-up, you get newly-minted graduates with rose-tinted glasses on (thanks to their outdated social theory models) being taken for a ride by clients who can recognise a soft touch ten miles off, you get no co-ordination, you get the massive, messy situations I see where – well, I can’t tell you because confidentiality but it’s heart-breaking to see the situations, know that children are being messed up, and know that in five, eight, ten years’ time these screwed-up kids will be repeating the same patterns because right now there is no meaningful intervention, no places of safety, no educational and psychological services, only very over-stretched social workers who can’t give the time, attention and care they need to give.
Believe you me, the toughest physics lab with the most high-pressure research load in the world is a lot, lot, lot easier by comparison.
possessing the social skills and insight to manage unimaginably difficult people
Yup. Not a social worker myself, but working in social housing provision in local government.
We have clients who are paranoid schizophrenics (officially diagnosed with consultant’s letter on file) and dealing with them when they’re off their meds is something that needs a lot of tact and careful handling (and of course, giving us actual training in this to let us do our jobs better? Ha ha ha ha ha!)
We have the common-or-garden depressed, suicidal, self-harming, social anxiety/social phobia, plain anxiety clients, as well as those suffering from physical conditions and disabilities.
We have the violent and likely to be verbally and physically abusive (one guy last week broke the office door on the way out because he was dissatisfied with the answer he got to his query).
We have the outright criminal element.
We have the people trying to get out of situations where they fell in with the criminal element.
We have the ordinary low-income/unemployed/in need of social supports people on waiting lists for five years or more, but the money ain’t there because with the Great Irish Economic Collapse Death of the Celtic Tiger of 2008-2010 and the years afterwards of austerity, there was no social house building programmes and so we’ve nowhere to house these people until our current tenants die and houses get freed up.
We have people who are in the grey area of “are they fantasising or is this really happening?” One client is mentally unwell, cannot really distinguish fact from fiction, and regularly tells us in great detail tales of woe about childhood abuse (which may have happened; just because she is fabulating other things does not mean this is untrue) and is now wanting a house transfer because she claims her life has been threatened: certain persons have gone around with a gun showing it to certain other persons and said they will shoot her.
Which may indeed be true, because the certain persons she is alleging this about are known to us and the police, and they have committed violent assaults causing actual bodily harm (as well as being involved with drugs and crime). Also I know one of the parties involved from my previous job in education and yeah. I can attest to her downward spiral.
So we can’t just say that “It’s all in her head, she’s crazy” even though she is not mentally stable and does invent stories which she believes to be true reality.
Scott, who is working at the coalface in a public hospital, probably recognises all this.
I don’t know if this counts as “lower pressure” than working in a university research laboratory 🙂
I maintain there is still more social pressure on women than on men to devote time to their families (indeed, to have families) in equal or greater amounts than their careers, and that something has to give.
Women do a lot of emotional/social support work that is not acknowledged, and by that I don’t mean “nagging their boyfriends/husbands to do the vacuuming when the house is adequately clean”. I mean women take up the slack in keeping connections open, keeping the family memory (who married whom, whose birthday it is on what day, how exactly is Auntie Mary our aunt? , no you can’t take Susie with the other kids to McDonalds for a burger and chips because she’s coeliac), make the doctor’s and hospital appointments and ferry various family members there, etc. etc. etc.
And that’s why women go into part-time jobs, flexitime jobs, careers where you trade advancement reliant on being there all hours and available at a minute’s notice for being able to schedule time off in an emergency because your mother-in-law missed the bus home and has to be picked up from the hospital fifty miles away and she just rang you rather than her son who works in the same organisation as you do (true story from my work place this week).
Like your housework example, though, you are probably overlooking a genuine gender difference in priorities. Men are simply less interested than women in maintaining “family memory” and robust extended-family connections. It isn’t obvious to me that men’s priorities are wrong and women’s are right, which seems to be the underlying assumption in claims that men aren’t pulling our weight.
And then you have an atomised society of individuals where there are no connections other than the temporary, family begins with your parents and ends with yourself, you can end up living alone and forgotten, and we get young men lashing out violently because they lack all means of achieving meaningful personal bonds outside of the sexual/romantic by “getting a girlfriend” and if women won’t date them, they are invisible and useless by their own and society’s opinion.
You may not think you need to know about Granny Joan’s arthritis, but when you end up in hospital and they’re asking for medical history and “any cases of this in your family background?”, you might be very glad to be able to phone your mother and ask her “Hey, did anyone in the family ever have diabetes/arthritis/this weird rash they can’t assign a cause to?” and get an answer other than “it is not obvious that maintaining family memory is beneficial so I never bothered listening to the oral history at family get-togethers”.
But if women’s priorities win out, we’ll have a society where everyone is too busy attending their third cousins’ bat mitzvahs to do any work, and we’ll all starve!
C’mon, let’s not play these silly games. We’re talking about decisions with small differences in marginal utility.
I agree with you that Deiseach’s reply is off-point (“But I like families!”), but I think you’re wrong. Men generally seem to like having a network of relatives, like having children, like their relatives to be in good health, like stable supportive relationships they can fall back on, like the state that results after conflicts are resolved. I’m not sure I can prove these are true, but I can prove they are cultural tropes.
We just don’t seem to put in the effort; we either get women to pick up the slack, act like it’s not worth it but then regret it, or somehow get pressured into it and then are happy with the results.
> I maintain there is still more social pressure on women than on men to devote time to their families (indeed, to have families) in equal or greater amounts than their careers, and that something has to give.
Is this substantially different from the proposition “There is more social pressure on men than on women to sacrifice their time with their family in order to advance a career that will provide for that family?”
If so, why do you exclusively phrase it in terms of what women are pressured to go and how the choices women make are only due to forces being inflicted upon them, while leaving it implied that men are not facing any pressures or having their choices affected even though they are?
I’m not Deiseach, but to me it seems entirely reasonable that they focused on the women-and-career* aspect of gendered pressures in a conversation primarily about gender and careers. If the conversation had been about gender and families, then your point about career-over-family pressures on men would’ve been equally relevant.
FWIW, I think I agree that both the pressure on women Deiseach described and the pressure on men that you described exist and are problems. I just think that it’s silly to attribute anti-men implications to Deiseach’s post when there’s a much better explanation for the emphasis they chose.
*the pressures Deiseach described are about women and family, but the point was that they affect women’s career choices
> Do the empathising career fields run at lower pressure than the systemising ones?
No, but median time spent at an employment opportunity should be significantly higher. Any job that needs familiarity and trust will benefit from long-term employment, while the STEM world is more effective when project-shaped.
And if you’re planning for kids, the long terms gains a lot of weight. Maybe women plan for kids more than men do?
My sample is crazy biased (my friends taking STEM classes), but this passes the ocular trauma test. All the people raised female had a strong opinion of whether they wanted children; most of the people raised male hadn’t really thought about it. This was a stronger predictor than gender currently living as.
There’s lots of possible explanations, but an obvious hypothesis is that when you’re capable of pregnancy (or expect to be but later learn you aren’t), you have to think about it. If you’re having sex, you have to avoid it; if you want to have kids, you have to (think about it and decide you’d rather adopt, or) plan for a time when you can handle pregnancy putting you out of commission, and make sure that happens while you’re still fertile.
Anon was me.
You appear to be using all GRE testers, which strikes me as not very useful. If you are only using US testers, then you might want to mention it. (apologies if you did and I missed it).
I’m not happy with the use of GRE scores anyway–first for reasons that Jacob articulated, but also because there’s a huge skew in the scores. Many graduate degrees requiring GRE tests are attractive to a predominantly female population (elementary school teachers, nurses, social workers) who come from the 50th percentile or lower–that is, who can be considered to be *below* the average IQ of a college graduate. Male testers, on the other hand, are usually getting master’s degrees in subjects where the average degree-holder is considerably above the average IQ of a college graduate.
This is why female testers outnumber male testers in the US population–and that varies by race. In 2011, I see that 61% more white US females than males took the test, 147% more black US females , 40% more Asian US females. International testers, on the other hand, are 43% more male than female, and it’s a safe bet that both male and female international testers are skewed towards the “smart” grad degrees. And since 29% of GRE testers are international, that’s a non-trivial skew.
Of course, international testers bring up a whole nother problem, since they are mostly Asian and cheating like mad. The GRE had to stop using the question bank for the CAT and banned the computer version of the test in various countries because of Asian cheating.
So you’ve got two problems with using all GRE scores–they’re going to skew low for females because they have a larger chunk of 100 IQ testers and because the population more likely to cheat is international students, which are male. A whole bunch of smart people aren’t being included because they’re taking the GMAT, LSAT, and MCAT (speaking of STEM), and a whole bunch of really smart people who don’t have master’s in their particular field worth pursuing are being left out. Meanwhile, the single largest occupation in America, elementary school teachers, are taking the test simply to get it done, for non-selective schools, often to get the Master’s bump. (Secondary school teachers are a smaller group with much higher ability levels–50-75%ile of college grads, and also closer to 50-50 gender split.)
It seems to me that the enormous range of cognitive ability required in the master’s programs would make any correlation very much of a “duh”. You might want to start the comparison at Ev Bio, although I guess that might negate the point of your work.
Then you’d also want to limit your comparison to whites. Hispanics are a tiny group, and Asians have the aforementioned cheating problem (yes, here too) and a small enough population to make the cheating possibility problematic.
All of this may be why the SAT had less correlation than the GRE. You’re getting the whole population, instead of one skewed towards the top and the bottom of college grads, with the middle and a good chunk of the top missing.
It’d be interesting to do this comparison with MCATs and specialty area.
I don’t disagree that the most likely explanation is more smart guys with high spatial abilities. But I do think that we aren’t doing enough to develop our high verbal ability folk, and teach them math. One thing the new GRE did, as the SAT did before it, was erase the huge gap in high verbal scores by making the verbal test easier. Genuine high verbal scores are very rare and high verbal without corresponding high math also rare, as I understand it. Wouldn’t surprise me if the latter group is female.
Incidentally, you might want to call it the Voldemort View.
/
Oops–forgot a few points.
It may be that my concerns above are irrelevant–that is, using white US born testers would yield the same result. I just think it’s best to be sure.
Grades are worthless as ability indicators in high school, and probably worthless in college, in any absolute sense.
There was some discussion about what harm it does to consider these issues. Here’s a very real example that impacts black college graduate employment: Over the past 15 years, there has been an increased push to “improve teacher quality”. This push has been based on a number of false beliefs. First, that teachers come from the bottom third of college graduates, when in fact elementary school teachers come from the second quintile, and high school content teachers are comfortably averaging at 55-60% (SAT scores in their content area). Second, that smarter teachers lead to better student outcomes, when in fact the data on that is depressingly limited and what little there is tends to evaporate on closer inspection.
But bumping the credential test cut scores for elementary school teachers (they are already quite high for high school teachers) has done nothing to improve academic outcomes. Meanwhile, the higher cut scores have decimated the black and Hispanic teacher pool. Ironically, there’s much for support for the notion that kids do better with teachers of their own race than that they do better with smarter teachers.
So long as we keep cut scores high, the only way to increase the number of black and Hispanic high school teachers would be to pull them from other high IQ occupations that pay much better, and for elementary school teachers to pull them from medical field (non MD) occupations, which blacks seem to prefer. Or, we could lower the scores needed for elementary school and let more black and Hispanic teachers in.
But we can’t even discuss this, because to do so would mean that there wasn’t a “fix” for the lower black and Hispanic teacher scores.
Even more ironically, lowering the cut scores wouldn’t allow a flood of white teachers, because whites with the same SAT scores as blacks are far less likely to go to college, so they can’t be teachers.
So by refusing to acknowledge the achievement gap, we are closing off a career to black teachers.
Oh, and the idea that teachers are thinking “Yeah, he’s black, so won’t be good at math? Yeah, she’s a girl, so don’t expect mucfh?” Not that I’ve ever seen. Not in any systemic fashion. Society looks at group performance. Teachers look at individuals. Not because we’re morally superior. It’s just our job.
Various cites: 1, 2, 3, 4
> “Ironically, there’s much for support for the notion that kids do better with teachers of their own race than that they do better with smarter teachers.”
How does this reconcile with the school integration project?
Not sure what school integration project you are referring to, but the belief that integrated schools improve the achievement gap is just that.
However, I don’t think the data supports anything like “give all black students black teachers or dire results follow”. Rather, there’s more research establishing that (in particular) low income black kids do better with black teachers than there is showing that high test scores make better teachers. And it’s evidence yet again that society tends to push prescriptions that sound pretty even if they are harmful, and ignore data that flies in the face of our desired beliefs.
Scott,
(I apologise in advance for asking about something completely unrelated to the topic of the post.) I’d like to write to you (the old-fashioned way, via the post), but I don’t know where to address letters to you. Should I use the address you gave for the October 2014 LessWrong meetup – is it still current?
Yes, but I will be much less likely to read or respond to snail mail in a reasonable amount of time. If you’re thinking it will be some signal that makes me more likely to pay attention (like they say about Congressional representatives) I’d like to nip that in the bud.
I want to write for two reasons:
a) I’ve noticed I think more clearly when writing longhand, and
b) I don’t know of any other way of contacting you that isn’t public.
(c) (Not relevant, but I’m putting it here for the sake of completeness and honesty) I enjoy it more.)
(I was aware that writing the old-fashioned way may have signaling value, but I don’t think that’s a real factor; the primary reasons are the ones I stated above. If there is another way I could contact you in private, I can write what I want longhand, and then either scan it or type it out.)
He has an email address.
FYI (and you may already be aware of this.) Untitled was referenced in a Conor Friedersdorf piece in The Atlantic:
http://m.theatlantic.com/politics/archive/2015/01/the-blog-comment-that-achieved-an-internet-miracle/384539/
You may find it interesting independent of its reference to SSC. Conor makes good points in the comments section as well.
Scott knows. And he’s NOT happy.
I hear Scott’s frustration that his post about a hot button topic gets mainstream media reference whereas much of his other, excellent work is engaged with less. Friedersdorf is arguing for intellectual charity and better dialogue. These are things Scott, himself, supports. Friedersdorf doesn’t misrepresent him and writes about Scott admiringly.
I think Scott is mistaken when he says that his other work has been ignored. “The Atlantic” didn’t ignore him. “The Atlantic” was unaware of him. Rightfully or wrongfully, “comment 171” drew mainstream attention. Conor Friedersdorf probably never heard of or was only dimly aware of SSC until the events associated with “comment 171”. I suspect he read Untitled and was impressed by what he saw. He used that piece as a stepping stone to argue in favor of decency and fair exchange of ideas in online debate. This is a Good Thing that Friedersdorf is arguing for. (The comments section appears to have devolved into something fairly awful. That’s… sad.)
I’m don’t know if Scott wants a larger audience (If I had to guess, I’d suspect he is conflicted about it and is anxious about the downstream consequences.), but attention he garners from his arguments about contentious topics may draw attention to his arguments about important, less contentious ones**. This would probably also be good for the world. Whether it would be good for Scott given the distress it could potentially bring him is for Scott to decide. He runs real emotional risk when he posts about topics that could bring him negative attention. I, for one, do appreciate that he takes that risk and honor his requests to keep his writing off of Reddit and etc.
**(For one thing, I’d love to see more physicians internalize his approach to patient care. Scott has the spirit of an old time doc (maybe way old school, back to Maimonides 😉 ). I admire that.)
As remotely blurred pointed out, Connor Friedersdorf had previously written in the Atlantic about Scott.
Your predictor variable is percent of gender by major. But we already know that more women are in undergraduate majors that require less math. You have not shown, in the least, that it is gender, and not the number of math classes taken that predict GRE math scores. I think it’s pretty reasonable to expect such an analysis to take into account the number of math courses required by major. Otherwise, your current argument is of this form:
Innate ability determines math GRE scores. Therefore we don’t need to consider training as an undergraduate in math when we do our statistical tests to determine whether innate ability determines the math GRE scores.
Basically, you built this circular logic into your statistical test. I can’t point you to a simple explanation on the web of what you did wrong but it is related to using correlated variables — which is something taught in an introductory class to linear regression. What you’ve done is a little different since you mashed two-correlated variables into one variable and then declared only one part of this mixed variable to be the determining factor. Citing someone doing an ANOVA is also not meaningful since the error is baked into the numbers.
The post explicitly considers this and uses SAT scores, untainted by college math classes.
No one really mentioning that Leslie et al don’t account for the proportion of non-alien students in graduate programs? That’s the first and most fatal flaw in all of this, actually. It may be insignificant enough at the undergraduate level in many cases but it’s not in graduate school. Proportions also vary tremendously across fields.
Basically everything should be nearly thrown out when you’re not considering American citizen students (eg. foreign students who come to graduate programs will not necessarily have taken the American SAT in high school). There’s not enough evidence to disprove hypotheses, when dealing with foreign students, that who takes the exams along with their performance could easily be influenced social and cultural pressures, rather than truly representing the innate talents of the underlying student population.
Of course the data for US citizen/resident students will reflect the same general conclusions reached by the blog post here, but it’s really really really really necessary to clean it up that way first. What needs to be presented is, say, GRE scores for American citizen students, and proportion of graduate-level American citizen students which are male/female in mathematics/all other fields. That information is not what is naively being presented in discussing this paper and so we’re looking at large distortions. Unfortunately public datasets may be lacking in this area, but then everyone is blowing smoke both ways arguing about things which aren’t truly the real facts and statistics that are needed. There probably is too little data that on a case by case basis you can’t always show that a particular university or even subject field may not be unfairly favoring male or female foreign students in one way or another.
Edit: Just for politeness apologies if I missed any other commenters on the extensive thread because ctrl-f for “resident,” “citizen,” and “alien” turned up nothing major. I did check that statements in the blog post like “The average man gets 154.3 ± 8.6 on GRE Quantitative. The average woman gets 149.4 ± 8.1.” do not reflect the US citizen/noncitizen split as found in the ets pdf and when dealing with the sort of heteroskedasticity that’s present Scott should be aware that plugging and chugging into a few simple calculators for normal distributions and regressions doesn’t really give you perfectly true results.
Good post in general. But it gets a bit story time at the end, for example when you suppose that the major reason people think they want to major in physics in 11th grade and don’t end up doing it is dropping out.
I would venture that probably the far more common reason is that people don’t know what they want in 11th grade. Maybe they take a philosophy class or math class or some other subject their freshman year and find it interesting. I’m my own experience people tended to major in subjects where they bumped into a particularly inspiring professor early on.
Or maybe people decided they didn’t want to be I’ve in poverty for the next decade and a half as the go through the college masters phd post doc low ranked professor track and switched their major to CS or Econ. I also know many people who enjoy being paid.
The drop out causal path seems very inaudible to me.
“6. It’s hard to correlate SAT scores with majors, because the SAT data is full of tiny vocational majors that throw off the results. For example, there are two hundred people in the country studying some form of manufacturing called “precision production”, they’re almost all male, and they have very low SAT scores. On the other hand, there are a few thousand people studying something called “family science”, they’re almost all women, and they also all have very low SAT scores. The shape of gender*major*SAT scores depends almost entirely on how many of these you count.”
In a situation like this, I believe you can just weight each major by the number of people in it, and do the correlation that way.
“Precision production” is metalwork, running a lathe. It’s skilled, but it’s vocational training so an academic-oriented test would give low scores. “Family science” I haven’t a clue, but it sounds like child care/care assistant – again, a vocational course but you can go on to do third level studies and get a degree if you have the academic ability; quoting from similar type courses (I imagine) that my last place of employment oversaw:
I think “family science” might be the subject formerly known as “home economics,” based on my having seen it called “family and consumer sciences.”
I’m sorry to leave self a self absorbed comment, but reading this really upset me and I just need to get this off my chest… How is a person supposed to stay sane in a culture that prizes intelligence above everything else (especially if, as Scott suggests, Human Intelligence Really Is the Key to the Future) when they themself are not particularly intelligent and, apparently, have no potential to ever become intelligent
Right now I basically feel like pond scum…
I don’t know. Discussions of intelligence always make me very sad. Even discussions that make some people feel good about themselves. I was reading that a large percentage of people have extreme difficulty adding fractions. I personal find fractions pretty simple to grasp. But reading about people struggling with fractions make me wonder “what things do I struggle with that a truly intelligent person would find trivial.”
From the right perspective we are all idiots (except Von Neumann types). We just need to get used to being dumb I think. Being dumb doesn’t stop one from enjoying and getting meaning out of life. We can still drink coffee and eat chocolate and love our friends and family. I hope this is enough.
Wow. Congratulations, Scott. Now your readers who aren’t von Neumann are becoming convinced that they’re about as useful to humanity as the average dog 😀
Except for the chocolate part. Please don’t feed dogs chocolate.
I find fractions rather annoying. Possibly less because I’m stupid than because I grew up with the metric system where fractions are pretty much optional and as such never got any practice. I would rather calculate the slope of a random polynomial than add 1/17 to 1/29 any day.
When it comes to being useful, I don’t see it as my job to solve existential risk. My job is to help implement the solutions as they come along so that the smart guys don’t need to waste time worrying about implementation details.
I’m OK with that.
I find it easier to turn fractions into decimals and work with them that way, then turn the answer back into fractions if I need to 🙂
“This piece of wood is 3/4 of an inch in width and I need to cut it in half. Where do I make the mark? What’s 1/2 of 3/4? Well, first you get the common denominator – ah feck it, what’s 0.5 of 0.75? Okay, got it! That’s 0.375 which, when I turn it back to fractions, is 3/8 of an inch!”
This of course only works if the denominator is not coprime to 10. Then again, it’s not entirely coincidental that all the numbers in your example have that property; in many real-world applications such numbers are used because they’re easier to work with.
Hey. A lot of people here do prize intelligence over anything else. You see it on this thread, you see it on other threads. It’s just a subculture thing though. It’s a bunch of nerds placing a high value on their own aptitudes.
And in one sense there’s nothing wrong with that (every subculture does it), but there is definitely nothing objectively right about it.
Scott posted a link a while back to the story of the highest-IQ man in the world, who was working in NASA at eight, and then went back to his own country to live an unremarkable life. He didn’t think intelligence was the most important thing. He should know.
I don’t want to expand too much on this theme as it’s probably a bit rude to go on and on about how I disagree with the values of the community. I’ll just say I posted upthread about a friend of mine who is a social worker.
My friend’s ability to handle that job is something I personally admire more than I have ever experienced myself admiring anyone’s analytical intelligence. And I have got a MUCH higher propensity to admire intelligence than the average person, even though it’s low compared to the average person here.
Life isn’t fair. Sorry, but there it is. Most of us have to come to terms with the fact that we won’t be contributing significantly to the intellectual development of the human race. We won’t come up with the Theory of Everything, or cure cancer, or write the Great American Novel. (Side note: Our gender is probably not a big part of the reason.)
If you struggle a lot with this fact, I’d suggest thinking about the ego; what it actually means for one person to be “better” than another, and why we care about it so much. I’ve found Charlotte Joko Beck’s books Everyday Zen and Nothing Special very helpful on this topic, even for non-practitioners of Zen.
I don’t know if it’s as much of a consolation for you as it is for me, but keep in mind that intelligence is not monolithic. Intelligence definitely isn’t limited to analytic intelligence, as some people assume. It took Scott a long time to understand that he didn’t lack intelligence just because there were people out there that were better than him at a subject he admired (he’s especially cited maths as an example for this).
What I’m trying to say is that trying to measure intelligence with a single measuring stick is bound to be inaccurate, and looking toward others (especially people you respect in contexts they are most comfortable in) can easily make you think you’re much less intelligent than you actually are. Part of the strength humanity as a whole has is because we’ve learnt to specialise, which means some select people will be good at some things that most other people are not good at – but there are so many different subjects to specialise in that this means most people are bad at many things and good at maybe a handful of them. Most supposed geniuses will really not appear intelligent at all when you drag them out of their field of interest/expertise.
Against all odds (hereditary), I’ve come to nurture what I think is a decent empathic intelligence by now. I’m proud of that, because I know it smooths out problems people with less empathic intelligence might have in communicating with each other – a decent many times, I can explain motivations to people enough that they change their mind about whether someone is worth their contempt.
I can’t do maths. I can’t do languages. I can do enough comp-sci to make a living and be respected, but I’ll never design something revolutionary (don’t even have the drive, let alone the ability), and I don’t think it’s because I’m good at comp-sci (elaboration will follow). I know just barely enough about economics to help bolster my empathic intelligence, and no more. I definitely can’t do politics. I can’t do physics, biology or chemistry. (Biology would really interest me, but not a chance.)
And yet somehow, I still identify as a polymath, because I am pretty good at getting the general gist of things, regardless of subject matter. I basically have no chance at getting good at said subject, but I am useful to people in providing cross-disciplinary overviews of things. (Coincidentally, this is the trait that makes me be able to make a living in comp-sci.)
It took me a long time to accept that I’m intelligent – just not in the same way the people I admire are. By all means, I’m not the top of the crop in the cross-disciplinary and empathic niches, but I can accept I am doing an okay job.
While I can’t rule out that your situation is different, I’d imagine you’re in a comparable boat. Maybe poke your nose into https://slatestarcodex.com/2013/06/30/the-lottery-of-fascinations/ ?
For me, learning about intelligence is cathartic. I have deep-seated insecurities about being bad at math, and that if I were a good person I would study math more and be able to contribute to all of this amazing math and physics and computer research going on around me. Learning that mathematical aptitude is partly determined by innate factors is a good way of reminding myself that it’s not my fault, that I don’t have to exhaust trying to cram theorems into my head and then beat myself up when they don’t stick. It’s not my fault.
On the other hand, I am good at verbal skills stuff, and being good at things is also scary. And it’s also sort of cathartic to be able to tell myself not to get too arrogant about it. Like people are always complimenting my writing and asking me for writing advice, and I never particularly tried hard to learn to write, and I have no idea what advice to give, and so it makes me feel like a giant imposter. And being able to remind myself that I’m not an imposter, I just got lucky – that’s also cathartic.
If you think you don’t have any skills – well, first of all I doubt that’s true, I would be surprised if there were people who read all the way through the above article and understood the gist of it who aren’t above average in many domains. But more important, remember that Hsu and Schombert paper. In all non-mathematical subjects, greater effort can compensate for lower ability. Even in math, once you pass a certain ability threshold, effort will have important effects for how you do relative to other people at your same ability level.
If you’re like me, you know that you can’t do math at von Neumann’s level. You don’t need a study to tell you that. But the studies are pretty optimistic about your ability to do anything else.
Why would you think that writing is linked to verbal IQ? I’ve seen no evidence that writing quality has any link to SAT verbal scores. High verbal scores are linked with strong analytical skills, which is a different thing entirely. High verbal scores are far less frequent than high math scores.
I wrote about my learning math as an adult. People with high verbal IQs are almost certainly capable of learning math well. We are doing a better job of teaching them these days than we were 20 years ago or longer.
How are you operationalizing “writing quality”? (If you’re talking about the essay portion of the SAT, then I might agree with you. If you mean something else, then idk…)
How are you operationalizing “writing quality”?
For a start, not using neologisms like “operationalizing” which sound like big clunky lumps of slag rattling down the rusty rubbish chute to land in a noxious cloud of coal and rock dust on the despoiled side of what had been a reasonably picturesque hillside 🙁
Operationalizing is very clear imo.
Also it is douchey to write posts like that Deiseach. Don’t snark about how about people write please.
I . . . inspired . . . poetry.
Srsly, though, this is the anon who wrote “operationalize,” which is a jargon-y technical term that I’m very certain both Scott and Education Realist will know 🙂
“Also it is douchey to write posts like that Deiseach. Don’t snark about how about people write please.”
“operationalizing” is a word like skunk is a smell. It’s bloated, ungainly, all twists and turns like a heap of rotten bowel. It hits the ear like the wide end of a canoe paddle, and leaves the mind numb and buzzing with horror. If you could complicate it by just a few letters more, I’m certain that speaking it aloud would cause a fatal brain hemorrhage.
I apologize. But whoever coined “operationalizing” should apologize a whole lot more.
Then sir, madam or other, kindly give me a definition of “operationalize” that also explains why this particular ungainly clump of letters had to be invented, as no existing word, phrase or combination thereof could do the work?
EDIT: I note that this is a concept derived from physics. Given that the query was on the nature of what constitutes good writing, would not the field of literary criticism better serve to yield a term of art for such queries?
Or perhaps this is simply proof in action of “women go for fields such as literary criticism, men go for fields such as physics”, since I do think I have some small talent for the use of English, and a word such as “operationalize” (well called ‘jargon’) jars upon my mental ears and causes me to wince. In short, it is offensive to my lamatyalve.
A reasonable standard of fluent, mellifluous written and spoken English is the hill I will die on. I will snark, fight, quarrel, carp, criticise, and in general be an unpleasant person saying “this usage stinks” when the usage does indeed stink.
Thanks for the prose, Deiseach & FC.
The difference between “What do you mean by “writing quality”?” and “How do you operationalize “writing quality”?” is that the former question admits a suggestive or poetic answer, while the latter does not.
“How do you operationalize “writing quality”?” means “How exactly would you measure it?”.
Of course, LW-style rationalists do like to use technical jargon outside its scope, but since we’re talking correlations here, we won’t get far without numbers.
Unless we’re going to whip out a measuring tape and a weighing scales and take those kinds of measurements of a length of prose, I really don’t see how “operationalize” is a useful term.
We can stipulate the font size, font type, line spacing, and write on both sides of the paper using a Number Two HB pencil, but that won’t affect the quality of the prose 🙂
Ten Top Tips For Succesful Prose Writing! is the kind of thing that comes to mind when speaking about “operationalize”, but once again – spell your words correctly, be grammatical, and match your style to the topic are all very well as the parameters for the piece, but they won’t much tell you if it’s good, bad or indifferent.
You can have a piece that hits every bullet point on the prescriptive list of “How To Do Writing Good” and it could still produce, upon reading, an effect which is the mental equivalent of trying to wade through freshly-poured cement.
‘Good’ writing does rely on subjective evaluation, I’m afraid there’s no way around it 🙂
To quote a countryman of mine, Myles na gCopaleen from a newspaper column of the 1950s:
I . . . can’t believe one
littlemultisyllabic word generated SO MUCH discussion.Deiseach, it’s from psychology and the social sciences (AFAIK). And I was actually asking what kind of measuring tape and scales to use 🙂
http://en.wikipedia.org/wiki/Operationalization
Nita: I’m not an LW-style rationalist. I don’t do LW and I don’t identify as rationalist. Between you and me, I’m more of an SJ-style feminist.
Ah, but that is precisely why “operationalize” is useful. 🙂
It reminds us that no matter what method we choose, no matter how clearly we describe it and how perfectly we use it, the numbers we get will never reflect the “true” value or describe the full complexity of the phenomenon we’re trying to “measure”.
Deiseach, I couldn’t care less if you like the word “operationalize” or not. Writing a long post about how terrible someone’s word choice is shitty behavior. It is not ok to “snark” people out for writing in ways you don’t approve of. Its extremely rude bullshit.
Maybe you have your reasons to “fight” against words like operatinalize. But douching out someone’s writing is not an ok way to go about fighting this battle. People get hurt when people make fun of their writing. Please stop potentially hurting people over a word use peeve.
It should be clear that professional literary critics will not actually find Scott’s posts to be scrumtrellescent examples of English writing. What makes SSC good is a nuanced mix of clarity, rigor and tone. That three-word description doesn’t encompass the SSC Secret Sauce but it points in a certain direction.
Somebody without Scott’s IQ couldn’t do what Scott does because they wouldn’t see all the things Scott sees. Even if they were amazing at conveying meaning through language.
On the other hand, the world is overfull of people with Scott’s IQ (and higher!) who can’t empathize, can’t imagine how a typical reader is going to take something, can’t do humor, lack work ethic, lack curiosity, lack passion, lack any kind of artistic bent, don’t understand and have no interest in emotions, and possess character flaws that make them overly sensitive to criticism.
I’d say high verbal intelligence is therefor a necessary but not remotely sufficient condition to produce good writing.
totally agree.
The constant fear of coming across a problem and looking like/finding out you’re a charlatan is something just about every single one of my engineering buddies suffers from. I can personally speak to the cathartic nature of having some responsibility for being brilliant taken off your shoulders.
We just do what we do, and wonder why everyone makes a fuss out of it, and when we’re shown evidence that our scribbling are somehow vastly superior to other people, sheepishness is the more common reaction than pride. The double-edge sword of intrinsic ability is, if you’re well-adjusted, pride tends to stem more from effort than absolute accomplishments, but praise (and to be fair, true value to strangers) comes from objective results. So we just kind of awkwardly thank people and feel twisted up inside over it.
You’re not alone. And don’t worry about the Math stuff. You’re going to do a lot more to help the world than the average Joe, and even your above-average Steve-the-mathematician with your writing and your basic knowledge of statistics. Seriously, you parse through methodologies and correlations faster than a lot of the people who work in fields dedicated to doing just that.
I just love this post. I wish all the stupid rich guys (and my former boss – Wall St.
– several) could read this..but they’re all in nursing homes, dead, in prison, rehab, or still trying to matter after all these years. The 1980’s are so dead, and, now MEN and WOMEN need to figure out what the F is going to get us into the green light of economic development ideas for the USA to be up and up without destroying the environment in the USA.
I can tell you this much, anon – if you are not fucking up other people, you are doing perfectly fine. If you are fucking up other people, I don’t care how big a genius you are, you are pond scum.
The whole point of the bell curve is that the vast majority of us are going to be smack in the middle. Some of us will be out on the very stupid end, some of us will be out on the very smart end. But most of us, going around our everyday business in the everyday world, will be average. That being the case, it really is better to be nice than to be smart, because the average person has a much higher chance of being either an asshole to the other people they interact with, and increasing the sum of human misery, or being a decent person and not doing that, then they do of Curing Cancer, Inventing AI or Discovering Limitless Energy.
In other words, there are many, many more potential assholes and abusers out there than there are super-geniuses, and it is perfectly within your ability (saving any circumstances to the contrary) to not be an asshole or abuser, which is a choice that will make the world a better place, even a little bit.
When I was young, I had a younger brother who beat me at practically everything involving intelligence despite me having 1.5 years on him. We’re both much older now but at some point I learned to have it stop bothering me and feel proud of him. This attitude of yours *is* something that’s possible to change. “Life is not graded on a curve.”
Also, if it helps, purely selfishly speaking I think I might make myself dumber. I’d get laid more (highly intelligent people are significantly more likely to be virgins) and I wouldn’t feel as much responsibility for trying to help the world.
“I’m sorry to leave self a self absorbed comment, but reading this really upset me and I just need to get this off my chest…How is a person supposed to stay sane in a culture that prizes intelligence above everything else – especially if, as Scott suggests, Human Intelligence Really Is the Key to the Future – when they themselves are not particularly intelligent and, apparently, have no potential to ever become intelligent? Right now I basically feel like pond scum.”
If I can offer a thought or two, perhaps in the spirit of Scott’s recent answer, but coming at it from a slightly different angle. Imo, you might find a useful philosophical distinctions than can clarify things is the distinction between intrinsic and instrumental values. An intrinsic value is something that is good, not for its usefulness, but because it is or we see it as inherently good. An instrumental value is something that we value or say is good not for its own sake, but for what it gives us.
Now it’s an unfortunate failing of the human brain that if we perceive something is instrumentally valuable for a long enough period, there’s a part of us that can get a little mentally lazy and starts thinking that thing is intrinsically valuable. So the rule we made about not eating a certain type of meat becomes a ritual, or washing our hands for cleanliness becomes a pathological obsession.
Intelligence is such a just such a thing. We evolved intelligence to help us gather more food, to avoid predators, to protect and fight human rivals still outside our growing circles of cooperation. In our own lives, we’re constantly witness to the usefulness of intelligence – it helps us get better jobs, we can negotiate complex situations and challenges, we can invent new ideas or technology that makes people’s lives better. And so there is constant temptation to start viewing the instrumental as intrinsically valuable. At first this seems fine, but then as we consider a future where first the stupid, then us, then everybody are no longer useful, this fallacious worldview becomes depressing and dehumanising.
If you were to ask me for my own solution, it would be this – immerse yourself in a philosophy that clearly understands the separation between intrinsic and instrumental value. Immerse yourself in a worldview that doesn’t dress the instumental up and true value – be it Progress, or Tradition, or anything else. Be part of something that considers you inherently valuable out of the kinship and fraternity of humanity and of life on Earth. We still hold a duty to achieve our best, to pursue wisdom and intelligence as best we can. Yes, human intelligence, and the technology that comes with it, is indeed the key to our future, but in the end it is what it unlocks, and not the key itself, that really matters. The only philosophy worth having is one that seeks to unlock a future for what is instrinsically valuable. That’s my belief – a future for people like you and I, for the human species, for life itself.
How robust is the stereotype result? How well replicated is the result?
There are at least two papers of which I am aware that find no stereotype threat when you alter the design of the study in very reasonable ways.
First one finds no stereotype threat when there are financial incentives. The second paper is able to use a large real world sample of students who due to variation in the roll outs of new tests had some students which received gender primes in their test blocks and others who did not.
“Exploring the Impact of Financial Incentives on Stereotype Threat: Evidence from a Pilot Study” by Fryer, Levitt and List (2008)
“Sticks, Stones, Words, and Broken Bones” by Wei (2012)
Outside the realms of academe and media, most people use common sense and acknowledge that there are many gender differences, but that they should not be a basis for discrimination or stereotyping. It is unfair to individuals who are not at the heart of the bell curve and there are so many mitigating factors. Ordinary people are very aware that IQ and innate abilities in any field are only one part of worldly success, which also requires characterological gifts like drive, ambition, hard work, self-discipline, people skills etc., many of which they believe (whether rightly or wrongly is another discussion) are matters of personal choice and responsibility.
It seems to me the ideal would be old-fashioned (attempting to avoid tribal signaling) value of judging people as individuals, along with awareness of possible sexist errors in thinking. It’s okay with “drive-by country” people that boys are better at some things and girls at another. Cowboys compete in roping and cowgirls compete in barrel racing. It doesn’t require screaming sexism nor does it require shutting the less dominant gender out of a given field. It is just the way it is.
All these issues have become so contentious because of the interjection of money, power and politics. Each of the great accomplishments against racism and sexism in the middle of the last century and been distorted and abused by the desire to have a quota system that distributes the perks of unearned accomplishment through the assertion of power, whether it be academic power, media, or government regs.
Outside the realms of academe and media and outside the two coasts, it seems to me that most people use common sense and acknowledge that there are many gender differences, but that they should not be a basis for discrimination or stereotyping, and would have no trouble with the research results you cite. At the same time, people know that judging by groups, whether gender or race or religion, is unfair to individuals who are not at the heart of the bell curve.
They also understand there are many mitigating factors. Ordinary people are very aware that IQ and innate abilities in any field are only one part of worldly success, which also requires characterological gifts like drive, ambition, hard work, self-discipline, people skills etc., many of which they believe (whether rightly or wrongly is another discussion) are matters of personal choice and responsibility.
It’s okay that boys are better at some things and girls at another. Cowboys compete in roping and cowgirls compete in barrel racing. It doesn’t require screaming sexism nor does it require shutting the less dominant gender out of a given field. It is just the way it is. People self sort according to their inclinations and abilities. We don’t want social engineering to work on making all groups the same.
These issues have become so contentious because of the interjection of money and power via politics. Each of the great accomplishments against racism and sexism in the middle of the last century has been distorted and abused by the availability of federal money, grant money etc. Instead of leaving it to the marketplace of individual achievement, we have a quota system that aims to distribute the perks of unearned accomplishment through the assertion of power, whether it be academic power, media, or government regs.
It seems to me the ideal would be old-fashioned value of judging people as individuals, and avoiding sexist errors in pre-judging individuals.
“…nor does it require shutting the less dominant gender out of a given field.”
But that’s exactly what you’re doing when you raise kids to believe that some fields are for boys and some fields are for girls.
Boys rope because they are gifted with throwing ability, undoubtedly a key to survival for hunters. Girls excel at barrel racing because they excell at agility. Girls can and do rope if they want to most don’t.
Do we do that today? I think we reached a very high level of success on that in the last 50 years, and now suffer from entrenched interests who profit from the battle and whose zeal is creating more problems.
Pingback: L.J Zigerell | Female representation across broad academic field
Came for the Scott Aaronson post, found this. Dude, this is da bomb. Will be back, more regularly.
Stereotype threat is cited as a cause in the paper, but there is more. The authors cite Dweck’s book (in #9) as a source. The underlying research paper for her book is Mangels et. al. where experiments were conducted, but the results are obviously loaded which is probably why the paper itself was not cited.
The best way to refute this nonsense is refute the underlying study that is the real source:
https://web.stanford.edu/dept/psychology/cgi-bin/drupalm/system/files/cdwecklearning%20success.pdf
I haven’t looked into the growth mindset stuff too carefully, but what I’ve seen doesn’t look like obvious nonsense. You want to run me through what you’ve found?
I haven’t looked into it carefully, but Dweck’s theory seems like another example of unnecessary construct proliferation. I’d love to see Scott’s take.
Have there been rigorous tests of the theory where its explanatory power is compared to that of traditional constructs like intelligence and conscientiousness, preferably longitudinally? I’d like to see a behavior genetic analysis of it, too.
Another similar construct is “self-efficacy”, but it seems that it has little validity independently of intelligence and the Big Five. Moreover, self-efficacy is highly heritable, with no shared environmental influences.
Damn it, I was going to give an objection when starting to read this and then you brought it up unwittingly yourself. Basically, there seems to have been a study showing a slight increase in the percentage of female computer scientists in their field after choosing college majors. Which would speak for women to be underrpresented here, since one possible explanation would be how women who were going into the field despite the stereotypes would be more likely to stay in, while others, who were discouraged by the stereotypes, found their way in later with the opposite dynamics for men.
Alas, computer science is a field where you would expect more women even with your calculations. It would be interesting to have these numbers for other fields as well, though at least it certainly doesn’t look like women are fleeing from STEM fields rather than not entering them in the first place.
I only recently found this blog, and though I have found many of the posts here quite interesting this is the first one I felt compelled to comment.
First things first, I am a straight white male in my late 30, of a fairly high intelligence according to IQ, SAT, etc, both in terms of math and verbal intelligence, though I opted to forgo a university degree. Instead I chose a career in sales because I concluded early on that I could earn just as much as most educated professional’s (if not more) without having to invest time, money and effort into earning a degree, while retaining a greater control of my career path; a conclusion which has since been borne out by experience.
While I can not speak to the objective evidence or cite any research supporting the claim that women are more likely to be of average intelligence while men are more likely to be of either high or low intelligence it has been my experience that this is in fact the case. To put it simply, in my experience men are far more likely to be either dumbasses or geniuses while women are fare more likely to be average. That this could be a factor as to the sex imbalance in STEM fields seems to me to be a reasonable hypothesis.
However whether it is or not, I do not think that is the primary factor which leads to the aforementioned sex imbalance. Rather from what little research I have done the issue is not native intelligence so much as it is preference, Several researchers have pointed out that the sex imbalance in STEM fields skews heavily towards males in more affluent, developed, and egalitarian societies, and more towards women in poorer, less developed, and less sexually equal societies.
http://contexts.org/files/2011/05/what-gender-is-science-1.png
Furthermore, it seems that the more intentionally sex equal a society is the less likely women are to enter into, and graduate from STEM fields. For example I have read, though I can not seem to find the source, that the % of women who enter into or gradate from STEM fields in Sweden, Finland, Norway etc is lower than it is in the US, whether measuring the % of women in said fields against the number of men in such fields or whether measuring the % of women in said fields versus the % of women in all fields.
Indeed as the chart linked to above would seem to indicate the only countries in which women earn more than 50% of science degrees are almost universally poor, and are almost universally considered more sexist than the baseline for western society rather than less. This would indicate to me that the more freedom women have to pursue the degree of their choice, the less likely most women are to pursue STEM subjects, regardless of whether the lack of freedom is to due to economic, social, or cultural factors.
As an example I would like to pint to a specific type of video games, namely first person shooters such as COD, counter strike etc. That there are women who enjoy playing such is not in doubt, also not in doubt is that the vast majority of FPS enthusiasts are male. Some may claim that this is due to discrimination, but said argument seems to me to be irrational as sex can not have any influence on the outcome of a match. As to the “hostile culture” hypothesis, this can only come into effect in multiplayer matches, and even then only if the female in questions lets it be known that she is such, and even then only if she chooses to engage in chat (something I do not do simply because I’m not as good at these games as I once was and I have no interest in hearing a 12 year old boy gloat after he kills me) However, despite the fact that video games are by their very nature sexually egalitarian (meaning that sex difference can not have any bearing on the outcome of the game since physical difference have little to no bearing on how good one is at playing said games) very few females play FPS’s simply because far fewer females have interest in killing several hundred electronic enemies than males do. IOW, the reason there are fewer female FPS gamers than males is because the genre is more appealing to most males than it is to most females. Its about preference.
By the same token, while there are probably many women who have either the interest or the aptitude to major in STEM fields, there are relatively few who have both.
As a result it seems to me that efforts to “nudge” more women into STEM fields are not only sexist against men (in that while the sex imbalance in STEM courses are seen as negative the sex imbalance in virtually all other degree courses is seen as either neutral or positive) but also sexist against women as it implies that their preferences are wrong, and must be corrected.
Furthermore, it strikes me as particularly insulting to women as it seems to suggest that they are too stupid, to timid, or too easily influenced to engage in the study of fields which tend to be more lucrative and/or more prestigious; rather than accepting that they are simply making a choice to go into a field which (while possibly less lucrative and/or prestigious) seems to be more fulfilling.
Furthermore every single hypothesis I have seen advanced by feminists to explain the STEM sex gap (and in truth virtually every sex gap) seems to paint a picture of women that is far closer to the views held by fundamentalist Muslim’s than what you would expect from those who claim to believe that women are the equals of men. IE that women are weak, timid, easily influenced, do not know their own minds and can not be trusted to make their own decisions.
Whats more is that this seems to be a trend. Whether its the “anti-manspreading” campaign, the “anti-street harassment” campaign, the campaign to “nudge” women into STEM subjects, the refusal to consider women’s aggregate choices in employment as it pertains to the “wage gap”, or the unequal treatment of males and females regarding alcohol and its effect on sexual consent, the underlying message seems to be that women are fragile, weak willed, victims who can not be trusted to make their own decisions or bear responsibility for their own choices. How such an attitude can be considered feminist i simply do not understand.
Going even further, I do not believe than men and women are equal, whether you define equal in the mathematical sense of “without difference” or you use the more colloquial definition of “having equal capabilities”; but it seems truly bizarre that those who claim to believe in women’s equality the most seem to see women as even less capable and resilient than I do.
Sir, when attesting to your verbal intelligence being toward the higher end of the scale of measurement, please do not subsequently use the Greengrocer’s Apostrophe.
(Was that bitchy of me? Then that was bitchy of me.)
Nothing of substance then?
Thank you for letting me know up front exactly how much attention to pay to your comments. I surely do appreciate it.
As I said upstream, I will fight and die about good English. Insults to my religion, nationality and politics I may let pass; sloppy English never.
Think of it as someone critiquing your slapdash statistics or mangled equations.
I see too much bad writing (and have had to turn extruded verbiage product into intelligible English for work purposes). I don’t mean plain lack of ability to spell (though I see more of that than I care to view) or fractured grammar; I mean chunks of what passes for prose produced by my superiors and by the government bureaucracy that is meant to convey a particular message and that is sodden, leaden, stiff and confusing. It fails of its purpose in communicating meaning. I have had to excavate the intended meaning and turn it into plain English that the public can read and understand, and I am not about to let any poor communication pass.
If you are going to vaunt your high verbal skills, demonstrate them. If you were trying to make a point dependent on the statistics Scott uses in this post, and you made an elementary error, would you expect that to be let pass without comment?
But this is exactly the quarrel I have with technical types who care little to nothing about the soft humanities subjects and it means that even when they have something important to convey, their inability to do so in a fluent and colloquial manner means they may as well be so many chirping sparrows for all the good they do with their written work.
You criticize my style of communication yet you still have nothing of substance to say. In my experience those who chose style over substance have neither.
Good day.
I don’t think those were actually grocer’s apostrophes (which are incorrectly used for emphasis). They seem to be scare quotes (which serve to inform the reader that the term within is considered by the writer to be of dubitable validity).
Mars used scare quotes but also used the greengrocer’s apostrophe, ie, inserted an apostrophe into plurals: “professional’s” and “Muslim’s”; and the controversial “FPS’s.”
I agree with other anon. If you keep posting this shit people should skip your comments.
It seems a good a place as any to link to Philip Greenspun’s tract (rant?) on women in science, where he says that women don’t enter science because they realize it’s a bad deal and men enter into it to impress their (probably not deserving) peer group.
Obviously there is much more than that, and Greenspun does tend to be very opinionated, to the detriment of accurate truth seeking.
Great comment. I’m going to try to answer some of your questions:
I think you’re reading something into these arguments that isn’t there — that the theories implicit in the arguments are only supposed to apply to women. I believe that the perspective is actually that men and women are similarly weak, timid, easily influenced, etc. but that due to prevailing cultural attitudes, men are “easily influenced” into more active, heroic roles and women are “easily influenced” into passive, support-type roles. The problem may be that you don’t realize that, to most of the people making these arguments, culture is supposed to be a much stronger force in shaping one’s preferences than anything intrinsic to the individual.
That is, the “feminist” theory here is that women have different outcomes (including different preferences) because they are socialized differently than men are. On this theory, women must be protected from memetic harm. Men don’t need this protection not because they are stronger than or less easily influenced than women, but because their socialization is presumed by the feminist not to be harmful.
Note, I am not making any judgment here about whether any parts of the implicit theory are true or not.
Assuming you meant, “anti-mansplaining”. This book was written before the author had heard of the term “mansplaining” (and in a forward written for a later edition the author mentions not thinking the term especially helpful). Anecdotally (and since you feel free to draw on experience to support most of your claims, I feel fine doing the same) it really does seem as though there’s a tendency for at least some men to underestimate the intellectual abilities and accomplishments of women. To the extent that this is a real phenomenon, it seems valid to me to raise awareness of it and to try to discourage it. Without a valid argument as to why I shouldn’t believe “mansplaining” is a real phenomenon or why it would be desirable for women’s intellect to be underestimated, I’m stuck with the impression that this is actually a legitimate feminist complaint.
“anti-street harassment” — A lot of women have an open stated preference that fewer men catcall, flirt with, or generally express opinions on their appearance in public. (I’ll appeal to your obvious concern with women’s preferences to make sense of why this is significant.) Again anecdotally, it seems safe to me to say that most of the men engaged in this behavior don’t do so as a result of unassailable motives. Applying social pressure (mostly shame since that’s the main vector for social pressure) to try to achieve one’s open stated preferences seems legitimate to me. It’s the same way we keep people from cutting in line or from taking all the donuts from the break room. If there was a legitimate argument that the sorts of behaviors being discouraged are actually useful to society in some important way I’d love to hear it.
the campaign to “nudge” women into STEM subjects – Again, I don’t think this is done with the intention of denying women their preferences. I think it’s done from the perspective that those preferences are primarily the result of socialization and that different sorts of socialization would give different preferences. Feminists perceive our culture as steering young women away from interest in STEM subjects and want our culture not to do that any more. Feminists aren’t saying young women must study STEM subjects. They’re saying they should be able to if they want to and they shouldn’t have to contend with anti-woman bias in addition to the challenge of STEM material itself if they so choose.
Feminists may be factually mistaken as to whether this is actually a good description of the state of affairs, but whether they’re factually wrong says pretty much nothing about their motives which I think are much different than you believe them to be. Since the feminist approach relies on assumptions that need to be empirically validated (and probably won’t be) I won’t argue as I did with your first two examples that this is a legitimate practice; still, I believe it’s helpful to try to understand the perspective of the person against whose position you are arguing.
refusal to to consider women’s aggregate choices — this is in some sense simpler than the other cases and in some sense more complex. The more complex way of looking at this is that, as above, those choices and preferences are (under a feminist’s way of seeing the world) at least in part the result of a process of socialization — if the woman had been raised differently she would have different choices and preferences. Feminists want to create a cultural environment in which women’s preferences aren’t constrained in the ways feminists currently perceive them to be. (Again, they may be factually mistaken but that won’t tell us much about their motives.) So it’s not that they’re ignoring the content of women’s preferences, it’s that the content of those preferences is itself the issue under discussion from the perspective of a feminist.
The simpler way to see this one is an instance of “all arguments are soldiers.” If feminists admit that the pay gap is the result of preferences (actually, they usually do admit this and then argue that the preferences themselves are a result of a sexist culture), then they have lost what looks like a pretty good argument for affirmative action for women.
the unequal treatment of males and females regarding alcohol and its effect on sexual consent – Most feminists I’ve seen writing on this topic will say that the rules are the same in both cases — whether it’s a woman or a man who is intoxicated, the result is still rape. (I suspect there are plenty of feminists who think that men cannot be raped by definitional fiat. Let’s ignore the complete idiots on both sides.) I think most feminists would argue that where such an inequality is perceived, that inequality actually results from unequal sexual aggression between men and women — men may be more likely to proceed in cases that are ethically ambiguous.
It’s only the last couple paragraphs of your comment I take any issue with, and even then it’s mostly just the fact that you seem to want to make a moral case against your opponents by (accidentally, it seems) misrepresenting their motives. Try to avoid this — it makes the argument you started out with look weaker than it really is.
This is unlikely; “manspreading” is a pejorative term that’s been going around feminist spaces recently referring to men sitting in seats, typically in public spaces, with their legs spread. It’s not really clear to me why this is even considered to be bad when the space isn’t crowded, let alone somehow sexist.
I doubt the feminists in question dislike men spreading their legs while sitting on a solo seat. However, a manspreader creates discomfort to the person sitting next to them (most women will let this slide despite being uncomfortable) and even if there isn’t someone sittingnext to them, it creates a disincentive for anyone wanting to sit there.
I looked at GRE scores by intended field a decade ago. I don’t know what the test is like today, but back then math scores averaged much higher than verbal scores. So, if you took the average standard deviations from the mean, treating math and verbal equally, the highest scoring fields were:
Physics & astronomy
Philosophy
Mathematical Sciences
Materials Engineering
Economics
In other words, the Genius Myth seems to be not a myth: the smartest grad students tend to go into traditional fields for big brains: physics, philosophy, math, and the upstart of the last 250 years econ.
http://isteve.blogspot.com/2007/08/graduate-record-exam-scores-by-graduate.html
Keep in mind that nobody could get ethical approval from their IRB to carry out a genuine test of stereotype threat in a high stakes testing situation:
http://www.vdare.com/articles/stereotype-threat-aka-occams-butterknife
Instead, stereotype threat studies are carried out in no-stakes testing situations in which the researchers signal to certain groups that they aren’t expected to expend energy on this pointless test.
(And then if stereotype threat isn’t found, the study seldom gets published.)
Wait, I may be behind the schedule: wasn’t it found conclusively that stereotype threat is a function of testosterone: high-testosterone, dominance-oriented, competitive people who want to do better than others get their performance reduced if they are told their group performs comparatively worse than other groups, while low-T people i.e. meek nice little girls who did not want to do better than others but simply well, were not affected by it?
I’ve never heard that one before. Source?
http://www.reducingstereotypethreat.org/bibliography_josephs_newman_brown_beer.html + you can google a bunch of journal articles “testosterone stereotype threat”
STEM as a category should be reconsidered. Writing code is a large part of my livelihood, yet I never learned much maths and don’t use it either. Consider something like making a “total sales per state and product category, this year, last year, % difference” report with an SQL query. This approximates the coding (OK: querying) part of my job just fine (although it gets more complicated than this). Most firms don’t need statistics or “business maths” or “business software maths” more complicated than this.
I would say the major challenge of my job is not the technical-mathemathical aspect, but finding my way of contradictionary, inaccurate, uninformed requests. Like “how much money did we make on product X” – what do you even mean, margin as sales price – FOB price, margin as sales price – total landed costs, sales price – total landed costs – marketing expenses and so on?
I would think that is more GRE Writing than GRE Quantitative, more empathizing than systematizing, more feminine than masculine?
Yet, we ERP Consultants have about a 70% male ratio.
I don’t think this is prejudice. I do think the job sucks enough that most women want a more sensible job.
Maths isn’t arithmetic. Coming up with an algorithm to transform data from some representation to another is.
There certainly are programming jobs that are not exactly high maths-skill, beyond the concept of representing some kind of processing using a formal language. I don’t know what the data is on programming jobs that consist of writing some SQL and sticking together some modules in some system vs programming jobs that entail coming up with algorithms, but the latter definitely qualify as maths.
Math, to me, is generally understanding something that was expressed in dry, abstract symbols. I always felt lost reading something like y + Δy = f(x + Δx) = m (x + Δx) + b = m x + m Δx + b = y + m Δx. Too “dense”, too “zipped”. Too abstract. Whenever we got examples where we could work from something less abstract from the real world (“find the height of the pole”) I fared better.
My example is all about understanding things expressed in fuzzy imprecise human language, and the construct an algorithm that is still not as scary as the above equation, it contains normal words like SUM, IF, THEN, GROUP BY.
(I would not hate the above equations even nearly as much if they would unpack it from dense symbols to normal words, like current_price + CHANGE(current_price) instead of y + Δy and so on. I want to buy a beer to the man or woman who made it a custom to never use single letter variables or function names in programming!)
My point is that it all sounds like my brain operates the way female brains are predicted to work, yet I am a straight male.
Ugh! Typical programmer — choosing clunky verbose strings over elegant, concise symbols.
I wonder if it has something to do with being a fast but not attentive reader. I.e. typical book reader, literature reader. Too much used to skim books that say with 500 chars something that in math could be said with 10.
I wonder if this a big part of the picture or not? For the math-minded, for whom every char matters, because there is a huge difference between +x and -x, the verbose style of literature, essays and liberal arts may be aggravating.
For the fast, not attentive, typical essay or book readers (skimmers) it is the part of having to pay attention to every single char makes math hard?
You’re right, those are two completely different ways of reading.
After spending too much time on Scott’s blog, I might get halfway down the page in a textbook before realizing I have to switch to math mode and start over.
For the fast, not attentive, typical essay or book readers (skimmers) it is the part of having to pay attention to every single char makes math hard?
When it was A’s and B’s and lines on a blackboard whose shape really mattered, a prof told me I had a natural math brain. When it got to unpronounceble squiggles, I was lost.
+ Bingo to your whole comment, and my defense of skimming is, a well written article should be readable on both levels: the skimming level and the (sorry) nitpicking / screaming halt / bogging down level that may never get past the first, er, … sentence?
First I skim to see whether the whole thing is (to me) worth closer analysis. Then whether the skimmed view is useful for what the writer was probably getting at with each paragraph/page/chapter; the larger context can help in interpreting the squiggles. If the skimmed view doesn’t even make sense at its own level … Poof!
“Bingo! To your whole comment”, says this skimmer.
To be fair to mathematics, it is a language and requires its own symbols. You have to learn it like any other language with its own grammar and alphabet.
My brain is simply incapable of grasping the ‘grammar’ of maths; I can mug up a few stock phrases (formulas that are the equivalent of “La plume de ma tante est sur la table”) but I can never get fluent in it :- (
So the amount of Affirmative Action US higher education presently has for women applicants to math majors is the right amount, in that it counterbalances the amount of sexism from people involved in that recruitment process?
On first glance this seems like a reasonable conclusion.
“The correlation between the percentage of doctorates in a field obtained by males and the mean Verbal plus Quantitative plus Analytical Graduate Record Examination (GRE) score for that field was 0.76, d.f.=44, P<0.001. It was inferred that men tend to earn doctorates in more demanding fields. It was also maintained that the findings are very consistent with the previous literature showing males having higher means on a number of different cognitive and aptitude measures, including GRE Verbal and Quantitative and Analytical scores."
Donald I. Templer, Marie E. Tomeo. Mean Graduate Record Examination (GRE) score and gender distribution as function of academic discipline. Personality and Individual Differences. Volume 32, Issue 1, 5 January 2002, Pages 175–179
http://www.sciencedirect.com/science/article/pii/S0191886901000228
All true, but that doesn’t tell us anything about *why* men choose those fields more often than women.
Doing what they are best at?
In any case, this study reinforces OP analysis of Leslie et al data, where the issue is the explanation of why certain fields chose men in larger numbers than women.
Alarm bells went off when we switched from total GRE to quantitative GRE: GRE scores didn’t correlate the way we wanted, so we took the subsection that did.
To be clear, I do think the move is legitimate, but I don’t think there was enough care/justification. This sort of move should be treated like manually overriding settings on a nuclear reactor; it might be the right thing to do, but every alarm in the place is blaring while you do it. Even if it’s as intuitively obvious as using quantitative GRE scores to predict STEM aptitude.
Did alarm bells go off when you read the original paper in Science and defined GRE as 2*verbal plus math plus something time writing?
They loudly went off for me.
Really? You read the paper? and you noticed that definition? So you can point to the passage where they do that?
As I said to you before: Try reading the paper now, even with the hint and see if you notice it.
Mu; I didn’t read the original paper. But SSC generally keeps a higher standard, and I’d like to keep it that way
Really, by ‘alarm bells’ I meant ‘a vague sense that an assumption is creeping in unscrutinized in a way that we wouldn’t let Science get away with’.
My example is something that Scott did let them get away with, because he never figured out what they were doing. It is a difficult balancing act, because criticism of assumptions produces an incentive to hide assumptions.
My (public) public high school was actually sued for gender discrimination against Men the year after I graduated: http://newsbusters.org/blogs/noel-sheppard/2006/01/27/if-male-student-sues-gender-discrimination-will-media-report-it
The suit was parodied on the Colbert Report.
I’m late to the discussion, but perhaps someone is still reading. There is an important point about occupational choice that every discussion of women in STEM has been missing.
There is a widespread belief that if two people are equally good at math, then to the extent that abilities affect occupational choice and in the absence of any other factors like socialization they should be equally likely to enter a math related field. This belief is false.
Occupational choice depends on something David Ricardo (1830 or so) called comparative advantage. It’s not just how good you are at math. It’s how good you are at math relative to how good you are at all the other things you might be doing.
Suppose you are a boy in high school getting 90% in Math and 70% in English. You sit next to a girl who is getting 90% in math and 90% in English. Which of you is more likely to take engineering in college?
The question isn’t “Why are there so few women in STEM?” The real question is “What else are boys going to do?”
The “males have greater variance in ability” story might help at the elite levels, but it goes the wrong way lower down. Men outnumber women in engineering programs from the Ivy schools down through the State schools right through community college and into apprenticeship programs for electricians. Lots and lots of women have the skills to be electricians. But they have alternatives. What else are those boys going to do?
http://pss.sagepub.com/content/24/5/770#aff-2
From the abstract:
Results revealed that mathematically capable individuals who also had high verbal skills were less likely to pursue STEM careers than were individuals who had high math skills but moderate verbal skills. One notable finding was that the group with high math and high verbal ability included more females than males.
This is a very interesting perspective. Thanks.
That’s pretty much why I’m going into STEM fields. I’m not good with people so I’m trying to be at least decent in other stuff. Not sure how well this will work out now.
It would be interesting to see if male conscription in South Korea gave women an advantage, or at least a head start, in STEM fields there. It seems possible that having two years diverted to military service would detrimentally affect men’s careers there in the same way that women’s careers are affected by childbirth.
Lots of countries have conscription. And 30 years ago, lots more did.
Conscription is very different from childbirth because it is at the beginning. Companies are afraid that women are going to abandon them. But by the time the company has hired the man, conscription is in the past.
Many fields value the young, but most value 30 year olds more than 20 year olds, so 3 years delay of military service is not a big deal at the beginning of a career. It is often said that academic mathematicians do their best work before age 30, so they might be concerned with the delay of military service, but I think this is really a caricature. I have worked with beginning mathematicians who had been conscripted in Korea, Israel, and Singapore, and no one cared about their age.
More figures in Cognitive Sex Differences and Mathematics and Science Achievement by Phillip L. Ackerman on the Spelke Pinker debate.
The AP exam scores are usually also different from the course grades given by the schools themselves and show the opposite pattern, i.e. fewer 5s and 4s while grades are mostly A and B.
For the fall in the SAT-V(and presumablly GRE-V) scores, see,
Schoolbook Simplification and Its Relation to the Decline in SAT-Verbal Scores
Donald P. Hayes
Pingback: linkfeast – 01/27/15 | hbd chick
As the study points out, and I think you agree with this, the STEM vs. non-STEM distinction is not a great predictor of female participation in a given academic field: certain sciences, like biology, have a high level of female participation, and on the other hand some fields traditionally thought of as a part of the humanities, like (Anglo-American) philosophy, are dominated by men. The more relevant distinction appears clear: women are absent from “abstract” fields like mathematics, computer science, and philosophy, and are more prevalent in “concrete” fields like biology, psychology, and the humanities. If so, based on my own human experiences, I think a very plausible explanation for this divide is that women are more moral than men, or at least care more about doing direct good for other people. So they choose those fields that benefit society at large. With human-body or Earth sciences, it’s clear how their advancement would help a lot of people out. But even look at the difference between the philosophy and English departments in your average American university: a philosophy professor will spend a long time grappling with a rather abstract problem, like whether numbers really exist, say, whereas an English professor can make her students read a text that brings up issues like injustice in contemporary society. Basically, it would make sense to consider what kind of lives women want to lead (and what kind of lives they ought to lead) when addressing how their career paths diverge from men.
I wouldn’t make the distinction between “concrete” and “abstract” fields. Engineering can be very concrete as well as very male-dominated. Rather, I see the difference between human (especially human behaviour) oriented and thing oriented. There’s also the argument that biology lies closer to humanities than other natural sciences (and is also more equal than female-dominated) while philosophy shares a lot of principles with math and metaphysics.
I would also have to contest the assertion that this shows how women are more “moral” than men. Their preferences tend towards more social interaction which correlates with direct affirmation of their efforts, which some philosophies argue isn’t really moral (although not amoral either). On the other hand, research in particular has a reputation for helping a great many people, while giving little in the way of direct feedback. I’m not arguing either gender is more moral, just that it’s hard to define and could be interpreted either way.
“Human-centered” (or “life-centered”) versus not is a similar distinction to the one I was trying to point out; but I think the point remains: it is the person who will devote his life to studying something far away from human lives who has to justify his life decisions in a world full of injustice and suffering much more than the person who focuses on issues more directly related to that suffering.
Sheeeesh! Like what is going on? I feel like I have reached the “realm of the weird” that we joked about in the early 1980’s! Forgive me for laughing somewhat, after reading SOOO many people posting. I’ll zero in with just SAT words (as far as what I read in the posts) I remember (or ruminate about) that streams from this blog: Pontificate; Unctuous, Bloviate, Supercilious, Superficial…came to mind as I read this stuff.
After reading some (not most- got boooriing) I will leave my ideas, with trepidation, that someone may still read between the lines: I totally believe that girls and boys in HS have different aptitudes and interests in math, engineering (IF…they have those classes available: very important) and computer science. And, the girls that have this aptitude in STEM, are in the minority. I am one, for several generations. And, have known several generations of women who were in this small STEM minority, but these women are the top in their countries today (not me) speaking about health, clean water, climate change issues, social policy, etc.
Men were/are more oriented to “tools” and women were/are more oriented to “survival.”
Can everyone just get along?
Pingback: Lightning Round – 2015/01/28 | Free Northerner
Pingback: Dylan’s Desk: Why Silicon Valley is still a man’s world - BluGry8MiDawg
Pingback: Dylan’s Desk: Why Silicon Valley is still a man’s world | 6News
Pingback: Dylan’s Desk: Why Silicon Valley is still a man’s world | OnlineNewsPortal
Pingback: Dylan’s Desk: Why Silicon Valley is still a man’s world | Automated Cash Software
Pingback: Dylan’s Desk: Why Silicon Valley is still a man’s world | 381test
Thanks for a very thoughtful analysis. Just wanted to let you know that I mentioned it (and linked) in a post on VentureBeat: http://venturebeat.com/2015/01/28/dylans-desk-why-silicon-valley-is-still-a-mans-world/#
Pingback: Dylan's Desk: Why Silicon Valley is still a man's world | VentureBeat | Entrepreneur - Trendingnewsz.com
Pingback: Dylan’s Desk: Why Silicon Valley is still a man’s world | SomeLearning
Pingback: Jordan Meyerowitz | Dylan’s Desk: Why Silicon Valley is still a man’s world
Pingback: Foam Glider Assortment (Pack of 72)
Pingback: Being smart, being judged smart | Logic Matters
Pingback: A week of links | EVOLVING ECONOMICS
Why am I not surprised by the fact that the lead author is in the department of philosophy?
How has no one commented yet pointing out just how bullshitty this post is?
Let’s summarize the main argument: you silly academia folks! Of course women are perceived as having less ability – they actually do have less ability, duh! Look, GRE scores! Look, SAT scores!
What about all the million ways in which they were treated differently for the 17 years before they took the SATs? That girls who express an interest in math are treated differently than boys who express an interest in math? That the expectations that teachers have affect how well students do (robustly demonstrated experimentally), and of course teachers have different expectations from boys and girls with regards to math (among other things)? Nah, let’s just ignore all that. We’ll talk about stereotype threat because it kind of sort of sounds like the same thing and hope no one notices (worked pretty well, actually!).
Same applies to IQ tests, by the way, since you bring them up. But even if IQ were a pure test of innate ability (and it isn’t), it’s not *perfectly* correlated with SATs, which is what you’d need to make your claim (otherwise, the imperfections in the correlation could be precisely the reason for the difference).
And going back to the SATs for a moment, it’s worth mentioning that women are less likely to guess on multiple choice questions. When they’re not confident, they’re more likely to leave a question blank than men are, and that ends up costing points. Nothing to do with differential ability – just confidence.
Also, since SAT scores are apparently the be-all end-all of innate ability, are you claiming that Black people have less innate ability than White people? I’d like to see that blog post.
And really, there was no need to be coy with the title. You could have just called it “I’m a semi-mathematically literate sexist, Motherfuckers”.
“Also, since SAT scores are apparently the be-all end-all of innate ability, are you claiming that Black people have less innate ability than White people? I’d like to see that blog post.”
My life has taken a strange turn over the past few years, that a sentence like this actually made me laugh out loud.
So, are you saying that GRE, SAT, and IQ test scores are uncorrelated with inherent ability?
Yes, I mention this about a zillion times in the post. For example:
“This use of “innate ability” is not the same thing as “genetically determined ability”…The effect of steretoypes, insofar as those stereotypes globally decrease performance. Even previous training in a field might represent “innate ability” under this definition, although later we’ll try to close that loophole.”
“These data do not rule out simply pushing everything back a level and saying that these stereotypes affect what classes girls take in middle school and high school. Remember, we using “ability” as a designation for a type of excellence, not an explanatory theory of it. This simply confirms that by eleventh grade, the gap has already formed.”
“Anyway, even if the pop sci version of stereotype threat were entirely true and explained everything, it still wouldn’t rescue claims of bias or sexism in the sciences. It would merely mean that the sciences’ reasonable and completely non-sexism-motivated policy of trusting test scores was ill-advised.”
“Even if the correlation between innate ability and gender balance turns out to be an artifact, Leslie et al’s correlation between perceived innate ability and gender balance is still an artifact of an artifact.”
If you want to continue commenting on this blog in the future, please read posts fully before launching the insults and curse words.
The real question in my mind is why Science, or the National Science Foundation would publicize this 10th rate study in the first place. And not just publicize — highly publicize. It seems like the inherent problems in the study would be obvious to anyone at first glance. There seem to be three choices:
1) actual inability of the editors to think clearly
2) deliberate promotion of junk science for political propaganda purposes 3) uncritical acceptance of any result that confirms their preferred beliefs.
It would be charitable to assume 3. Alas, I lean towards 2. You can’t prove deliberate dishonesty of course. But, in recent years ‘high impact’ scientific publications, like Science magazine, and Nature magazine, seem to have become nothing more than propaganda arms of the liberal ‘consensus’. About the only subjects you can trust them on anymore is the hard sciences — stuff like molecular biology, and chemistry.
As a general rule, social science studies published by high-impact generalist journals like Nature and PNAS are junk. The purpose of their publication is to make headlines, and scientific rigor and common sense usually take a backseat.
This one seems to me worse than usual. The neglect of the literature is, perhaps, par for the course, but defining total GRE as M+3xV I can only describe as fraud.
What nonsense. GRE prefers American white men, that is well known, so you can throw away your ‘research’. I don’t know about SAT.
Also, to say that these results are the non-stereotype threat scenario is simply silly. There is huge influence upon girls from the moment they are born, to not care about their ability to think and instead care about their cuteness. For boys the exact opposite.
Of course in a study where stereotype threat is measured they have to take an initial condition and see how much they can widen the gap by imposing extra stereotype cues. That does not mean that the initial condition was 0!
In the society we live in it is not possible to say whether women and men differ in intellectual abilities, because this is not a stereotype free society by far. By the way, if you look at for instance Iran, STEM fields are mostly occupied by women…so apparently it can also be the other way around. Perhaps women are the geniuses, but because society is adapted to men’s preferences men prevail. Have you ever thought about that?
Pingback: rndn comments on “(unknown story)” | blog.offeryour.com